光电二极管检测电路的工作原理及设计方案

　　在这个应用电路中，对运放有影响而未模拟的另一个重要性能参数是输入共模范围和输出摆幅范围。一般而言，输入共模范围必须扩展到超过负电源幅值，而输出摆幅必须尽可能地摆动到负电源幅值。大多数单电源CMOS放大器具有负电源电压以下0.3V的共模范围。由于同相输入端接地，此类性能非常适合于本应用领域。当放大器对地的负载电阻为小于RF /10时，则单电源放大器的输出摆幅可最优化。如果采用这种方法，最坏情况下放大器负载电阻的噪声也仅为总噪声的0.5%。

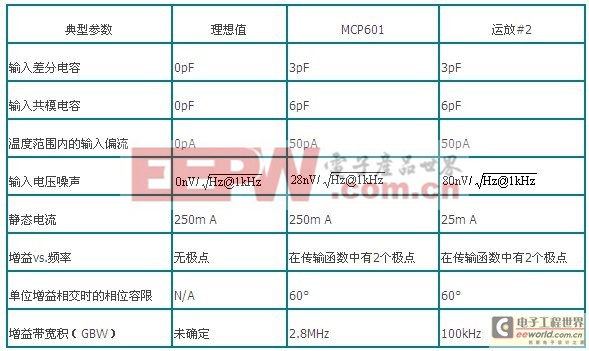
　　SPICE宏模型可以模拟也可以不模拟这些参数。一个放大器宏模型会具有适当的开环增益频率响应、输入共模范围和不那么理想的输出摆幅范围。表1中列出了本文使用的三个放大器宏模型的特性。

　　光电二极管和放大器的寄生元件对电路的影响可容易地用SPICE模拟加以说明。例如，在理想情况下，可以通过使用ISC的方波函数和观察输出响应来进行模拟。

　　2.3 反馈元件模型

　　本应用中应该考虑的第三个即最后一个变量是放大器的反馈系统。图4示出一个反馈网络模型。

　　在图4中，分离的反馈电阻RF也有一个噪声成分eRF和一个寄生电容CRF。

　　寄生电容CRF为电阻RF及与电路板/接线板相关的电容。此电容的典型值为0.5pF到1.0pF。

　　CF是反馈网络模型中包含的第2个分离元件，用于稳定电路。

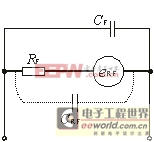
图4 图1所示系统反馈电路的

　　寄生元件模型

　　表1 本文提到的运放宏模型特性

　　将三个子模型（光电二极管、运放和反馈网络）组合起来可组成光检测电路的系统模型。如图5所示。

　　3 系统模型的相互影响和系统稳定性分析

　　当光电二极管配置为光致电压工作方式时，图5所示的系统模型可用来定性分析系统的稳定性。

　　这个系统模型的SPICE能模拟光电二极管检测电路的频率及噪声响应。尤其是在进入硬件实验以前，通过模拟手段可以容易地验证并设计出良好的系统稳定性。该过程是评估系统的传输函数、确定影响系统稳定性的关键变量并作相应调整的过程。

　　该系统的传输函数为

　　 （2）

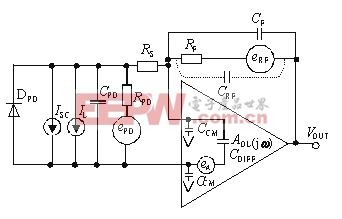
图5 标准光检测电路的系统模型

　　式（2）中，AOL（jw ）是放大器在频率范围内的开环增益。b 是系统反馈系数，等于1/（1+ZF/ZIN）。1/b 也称作系统的噪声增益。

　　ZIN是输入阻抗，等于RPD//1/［jw （CPD+CCM+ CDIFF）］;ZF是反馈阻抗，等于RF //1/［jw （CRF+CF）］。

　　通过补偿AOL（jw ）´ b 的相位可确定系统的稳定性，这可凭经验用AOL（jw ）和1/b 的Bode图来实现。图6中的各图说明了这个概念。

　　开环增益频率响应和反馈系数的倒数（1/b ）之间的闭合斜率必须小于或等于－20dB/10倍频程。图6中（a）、（c）表示稳定系统，（b）、（d）表示不稳定系统。在（a）中，放大器的开环增益（AOL（jw ））以零dB随频率变化并很快变化到斜率为 －20dB/10倍频程。尽管未在图中显示，但这个变化是由开环增益响应的一个极点导致的，并伴随着相位的变化，在极点以前开始以10倍频程变化。即在极点的10倍频程处，相移约为0° 。在极点发生的频率处，相移为－45° 。当斜率随着频率变化，到第二个极点时开环增益响应变化至－40dB/10倍频程。并再次伴随着相位的变化。第3个以零点响应出现，并且开环增益响应返回至－20dB/10倍频程的斜率。

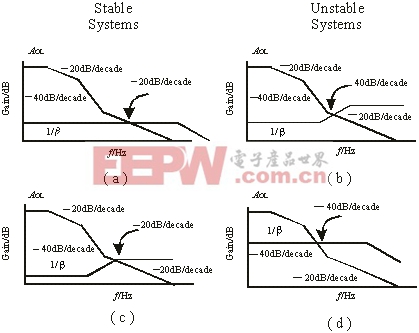
　　图6 确定系统稳定性的Bode图

　　在同一个图中，1/b 曲线以零dB开始随频率变化。1/b 随着频率的增加保持平滑，直到曲线末尾有一个极点产生，曲线便开始衰减20dB/10倍频程。

　　图（a）中令人感兴趣的一点就是AOL（jw ）曲线和1/b 曲线的交点。两条曲线交点的斜率示出了系统的相位容限，也预示着系统的稳定性。在图中，交点斜率为－20dB/10倍频程。在这种情况下，放大器将提供－90° 的相移，而反馈系数则提供零度相移。相移和系统的稳定性均由两条曲线的交点决定。1/b 相移和AOL（jw ）相移相加，系统的相移为－90° ，容限为90° 。从理论上说，如果相位容限大于零度，系统是稳定的。但实际应用中相位容限至少应有45° 才能使系统稳定。

　　在图6的（c）中，AOL（jw ）曲线和1/b 曲线的交点表示一个在一定程度上稳定的系统。此点 AOL（jw ）曲线正以－20dB/10倍频程的斜率变化，而1/b 曲线正从20dB/10倍频程的斜率转换到0dB/10倍频程的斜率。AOL（jw ）曲线的相移为－90° 。1/b 曲线的相移则为－45° 。将这两个相移相加后，总的相移为－135° ，即相位容限为45° 。虽然该系统看上去较稳定，即相位容限大于0° ，但是电路不可能像计算或模拟那样理想化，因为电路板存在着寄生电容和电感。结果，具有这样大小的相位容限，这个系统只能是“一定程度上的稳定”。

　　图6中（b）、（d）均为不稳定系统。在（b）图中，AOL（jw ）以－20dB/10倍频程的斜率变化。1/b 则以+20dB/10倍频程的斜率变化。这两条曲线的闭合斜率为40dB/10倍频程，表示相移为－180° ，相位容限为0° 。

　　 在（d）图中，AOL（jw ）以－40dB/10倍频程的斜率变化。而1/b 以0dB/10倍频程的斜率变化。两条曲线的闭合斜率为－40dB/10倍频程，表示相移为－180° 。

　　通过模拟可表明使用非理想的光电二极管和运放模型会造成相当数量的振铃或不稳定因素。在频率域内重新进行这种模拟会很快重现这种不稳定因素。

　　系统的不稳定性可用两种方法校正：（1）增加一个反馈电容CF;（2）改进放大器，使其具有差分AOL频率响应或差分输入电容。

　　 改变反馈电容。系统中影响噪声增益1/b 频率响应的有光电二极管的寄生电容、运放的输入电容，其阻抗以ZIN表示，放大器反馈环路的寄生元件，其阻抗以ZF表示。

　　ZIN = RPD //1/［ jw （CPD+CCM+CDIFF）］

　　ZF = RF //1/ ［jw （CRF+CF）］ （3）

　　1/b = 1+ZF/ZIN

　　噪声增益1/b 曲线的极点、零点如图7所示。开环增益频率响应和反馈系数的倒数1/b 间的闭合斜率必须小于或等于20dB/10倍频程。

　　在图7中，极零点频率如下：

　　fP1=1/（2p （RPD//RF）（CPD+CCM+CDIFF+CF+CRF））

　　fP2 =1/（2p RS CPD）

　　fZ=1/（2p RF（CF+CRF）） （4）

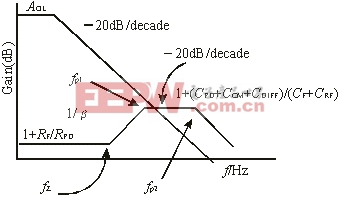
图7 噪声增益1/b 曲线的极零点图

　　从式（4）中容易地看出，加大CF将降低fP1，并降低高频增益［1+（CPD+CCM+CDIFF）/（CF+CRF）］。

　　1/b 网络的极点设计成1/b 与放大器的开环增益曲线相交的那一点。此时频率就是这两条曲线的几何平均值。CF可计算如下

　　 （5）

　　式（5）中fU是放大器的增益带宽积。此时，系统具有45° 的总相位容限，阶跃响应将呈现25%的过冲。对于使用MCP601放大器的电路，CF的值将为

　　这种最佳的计算结果是建立在假设放大器参数如带宽或输入电容以及反馈电阻值没有改变，二极管的寄生电容也无改变基础上的。

　　较保守的计算方法CF的取值为