PRC-CW雷达地杂波相关特性分析
E[A2i]=E[(xi+yi+zi)2]=3R(0);
2.不同波束在时间特性上是完全相关的
假定xi、yi、zi,…(i=0,1,2,…,N-1)分别代表不同波束的回波信号,i代表时间序列中的序号,并且,xi、yi、zi,…是完全相关的同分布的高斯N(0,σ2)随机变量,有:
E[x2i]=E[y2i]=E[z2i]=…=R(0);
E[xixi+τ]=E[yiyi+τ]=E[zizi+τ]=…=R(τ);
E[xiyi+τ]=E[yizi+τ]=E[xizi+τ]=…=R(τ);
Q个码元迭回后的序列为:
Ai=xi+xi+1+xi+2+…+xi+Q-1,i=0,1,…,N-1
则E[A2i]=QR(0)+2(Q-1)R(1)+2(Q-2)R(2)+…+2R(Q-1);
E[AiAi+τ]=QR(τ)+(Q-1)R(τ+1)+(Q-2)R(τ+2)
+…+R(τ+Q-1)+(Q-1)R(τ-1)
+(Q-2)R(τ-2)+…+R(τ-Q+1).
仍对相关函数进行归一化,并与没有发生码元迭加时的归一化相关函数相比较:m=E[AiAi+τ]/E[A2i]-R(τ)/R(0).求解此解析式,可得:
如果![]() 成立,则迭加后的相关性将增强,反之,相关性将减弱.分析脉冲雷达的时间相关特性,可知上述不等式都是成立的,所以,在有码元迭加的情况下,如果不同波束间是完全相关时,则时间相关性将增强,且增强的程度取决于上述不等式的差异.
成立,则迭加后的相关性将增强,反之,相关性将减弱.分析脉冲雷达的时间相关特性,可知上述不等式都是成立的,所以,在有码元迭加的情况下,如果不同波束间是完全相关时,则时间相关性将增强,且增强的程度取决于上述不等式的差异.
因此,对于PRC-CW雷达而言,由于码元和码元之间既不可能完全独立,又不可能完全相关,而是介于其中,所以其时间相关特性也应介于上面两种极端情况之间,也就是说,当码元回波发生迭回时,其时间相关性总是要增强的.
通过对相关函数作傅立叶逆变换或利用AR模型,就能得到信号的功率谱密度[5].
四、地杂波相关特性仿真结果
实验中对多种典型地物在PRC-CW雷达下的回波信号进行了计算机模拟,图3~图6分别示出在不同条件下的裸土和油菜的功率谱曲线,它们的空间分布参数及相应的空间相关系数参数、时间相关系数参数列于表1中,采样时间为25微秒.针对不同雷达工作参数得到不同的回波码元迭加次数,进行模拟得到PRC-CW雷达发生码元迭加时的地杂波回波复振幅序列Vg(t),再分析其频谱特性.
表1 典型地物杂波参数
| 地物 | 空间相关参数 | 时间相关参数 | 空间分布参数 | |||||
| as | b(m) | c(m) | at | α(ms) | β(ms) | 形参 | 杂噪比 | |
| 裸土 | 0.0 | 7.89 | 188.6 | 0.0 | 20.0 | 500.0 | 3.2 | 10dB |
| 油菜 | 0.24 | 0.30 | 90.16 | 0.60 | 10.0 | 18.0 | 2.9 | 10dB |
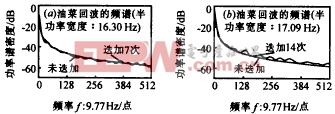
图3 |
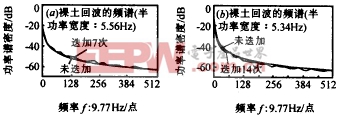
图4 |
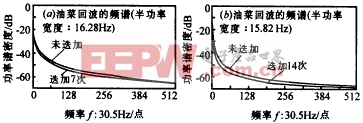
图5 |
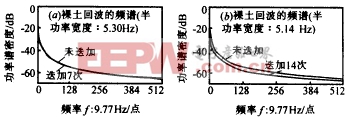
图6 图3、图4是以油菜和裸土为例,示出了当不同波束在时间特性上是相互独立的情形下,存在码元迭加时地杂波的功率谱特性,可以看出在一定的误差范围内,迭加前后回波信号的相关性及对应的功率谱密度曲线不变,与我们前边的分析一致. 五、结 论 |










评论