运算放大器的工作原理和原因，第 2 部分

运算放大器 （op-amps） 几乎是完美的放大器。只要你记住一些重要的细节，它们就会显得完美。

在第 1 部分中，我简要介绍了用作伺服放大器的运算放大器如何通过将小信号与放大器输出的衰减信号进行比较来放大小信号。我说放大器的作用是使反馈等于输入。当没有配置负反馈时，运算放大器具有极高的电压增益 – 可能是 100 k-V/V 或 1 M-V/V – 因此几乎是无限的。如果增益是无限的，则伺服作（图 1）将使负输入端和正输入端的电压相同。差分输入级将以差分方式放大输入电压（我们刚刚将其定义为零）并将其乘以无限增益，这将产生未知输出，因为它在数学上是未定义的。

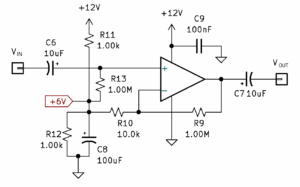
图 1.这是一个简单的单电源电路，在输入和输出处均具有 AC 耦合。电压增益

再看一下图 1，当您向运算放大器的同相输入（R13-C6 节点）提供一个小信号，将其放大一个非常大的数字，然后通过衰减网络（R9 和 R10）将输出（在 +C7）发送到运算放大器的反相输入（R9-R10 节点）时，伺服动作使电压差消失，但不是零。接近零与大 V/V 比的电压增益接近无限电压增益的程度直接相关。失真级别也与此有关。当然，完美的放大器不会失真。

我将在本文的末尾深入探讨这个问题，并让您进行数学分析。尽管如此，我希望这种简化和直观的方法能够建立一个理解框架。

输入结构特征

任何由双极晶体管、JFET、MOSFET 甚至真空管制造的运算放大器都会表现出不太理想的特性。输入级的主要缺点是输入偏移电压和输入偏置电流。在图 2 中，这是之前放大器电路的简化版本。为了简化输入偏置电路，它由双极电源供电。为清楚起见，省略了 output coupling capacitor 和 supply bypass capacitor。

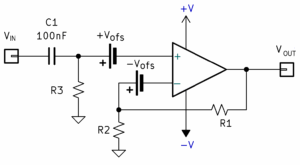
图 2.要了解真正的运算放大器，可以考虑一个完美的运算放大器，在差分输入端具有极少量的输入失调电压。

为了象征性地说明输入失调电压是什么样子，我们可以想象一个微型电池与完美运算放大器的输入串联，如图 2 所示。它们的端电压可能在几微伏到几毫伏之间。极性可以如图所示，也可以颠倒过来，具体取决于运算放大器输入结构的具体情况。

对于与交流信号一起使用的放大器，例如音频前置放大器、感应式转速计拾音器、振动传感器和 RF，偏移通常可以忽略不计。对于与直流信号一起使用的放大器，例如热电偶、光电探测器、静电计和电化学电池，请使用低失调电压运算放大器或添加电路来调整和消除任何失调电压。

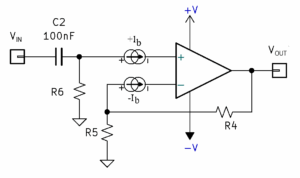
图 3.将真正的运算放大器视为完美的运算放大器，在差分输入端具有极少量的输入偏置电流。

为了象征性地显示输入偏置电流是什么样子的，我们可以在运算放大器的输入端添加微小的电流源，如图 3 所示。这些电流源的范围从毫微安到微安。它们的极性可能如图所示或相反，具体取决于运算放大器的输入结构。

该偏置电流将流过运算放大器输入端的电阻（因此 R6 用于同相输入，R4//R5 用于反相输入）。如果这些不匹配，则偏置电流流动和随后的 I-R 压降将有效地产生额外的偏移电压。如上所述，可能有必要将其无效。

带宽或频率响应

在解决了围绕运算放大器输入的主要问题之后，我们现在将注意力转向带宽规格。运算放大器的带宽通常表示为其开环电压增益（即不添加反馈），直到增益降至 1 或 0.0 dB 的频率。由于内部电路的低通特性，增益随着频率的增加而下降。通常由内部 capacitor 和相关的驱动电阻（即低通部分）创建一个主导极点，该磁极点会从频率滚降。例如，请查看德州仪器 （TI） 四通道运算放大器 LF444 数据手册的一部分，如表 1 所示。我在 spec 周围画了一个蓝色框，表示一个部分的典型开环增益。增益带宽积 （GBW） 显示为 1 MHz（典型值）。

表 1.LF444 一个部分的增益带宽积。（图片：Texas Instruments）)

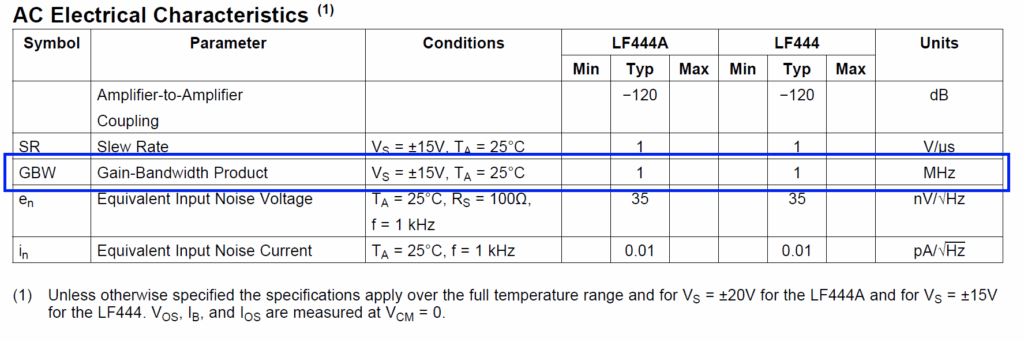
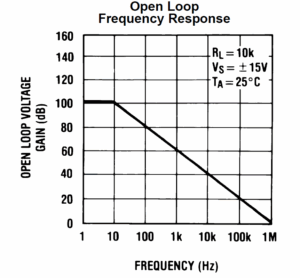
图 4.该图显示了 LF444 的一部分的开环增益与频率的关系。（图片：Texas Instruments）)

现在，参考同一数据表中的图 4，我们看到增益与频率的关系显示，从极低频率（可能是直流）到 10 Hz，增益与频率的关系为 100 dB。然后它以直线形式滚降，并在 1 MHz 左右达到 0 dB 点。因此，典型图表中显示的信息与表中的数据一致。请记住，x 轴（频率）和 y 轴（电压增益）都是对数刻度，因此 x 轴上的每个刻度线都是十倍频程（10、100、1 kHz 等），y 轴上的每个刻度线是 20 dB（20、40、60 等）。对数标度使我们需要执行的一些评估的数学作变得更加容易：您可以以分贝为单位添加或减去增益值，而不是以 V/V 为单位乘以增益值。

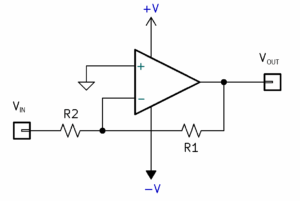
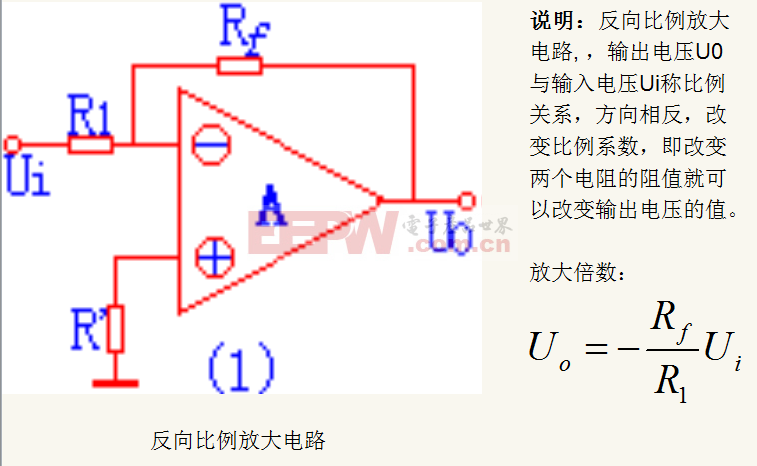
图 5.本例中，运算放大器的增益配置为 –R1/R2 或 –10 V/V。减号表示反相放大器，其中 VOUT 是相对于 VIN 测量的。

请注意，仅仅因为运算放大器的带宽扩展到 1 MHz 并不意味着您可以使用该运算放大器将信号放大到 1 MHz。嗯，你可以，但你不会对结果感到满意。为了了解原因，我们将深入研究运算放大器的工作原理，考虑闭环响应与开环响应的比较。

如果您想要使用增益为 10 V/V（相当于 +20 dB）的运算放大器的音频前置放大器电路，这是一个非常简单的电路。参考图 5，选择 R1 = 10.0 kΩ 和 R2 = 1.00 kΩ。

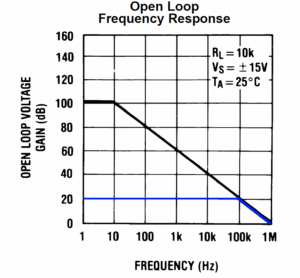
图 6.蓝线表示运算放大器电路的闭环增益。

要查看该电路将做什么，我们可以将 closed-loop gain 叠加在 open-loop gain 图上。如图 6 所示，我添加了蓝线。

从 V在到 V外，我们在 100 kHz 时获得 20 dB 的增益。然后，闭环增益将开环增益跟踪到 1 MHz，此时增益变为 0 dB（或增益 1 或 1）。对于音频来说看起来足够好，对吧？不。实际上，这是非常不可取的。10 kHz 时的增益裕量（开环和闭环增益之间的数学差异）仅为 20 dB，而 10 Hz 时的增益裕量为 80 dB。这意味着你会失真。

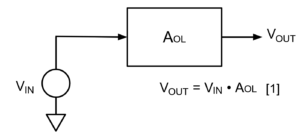
图 7.开环系统不使用反馈。

我们将重新审视伺服放大器设计的起点，以获得更好的理解。我们没有像图 1 和图 6 那样使用运算放大器符号和特定电阻器，而是在图中绘制块并添加必要的值来表示增益、衰减和信号相加的点（与运算放大器的差分输入结构相当）。因此，开环放大器和相关增益公式（公式 1）——称为传递函数——如图 7 所示。

transfer function 只是描述 output 和 input 之间关系的另一种方式。

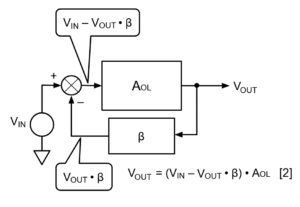
图 8.闭环系统将其输出信号的一部分反馈给其输入。

我们的目标是一个闭环系统，类似于图 1 和图 6 中描述的系统。我们可以通过绘制一个 block 并将其命名为 β 来使用更通用的反馈 resistor 表示。我们可以将差分输入表示为一个内部带有 X 的圆;这是求和结点的通用符号。参考图 6，求和结是 R1 和 R2 连接到运算放大器负输入的节点。闭环伺服系统如图 8 所示。

使用的一些术语是不言自明的，而另一些则不是。以下是所有术语及其含义：

• V在是输入电压。

• V外是输出电压。

• 一个老是放大器在添加任何反馈之前的开环增益。

• β 是 β Box（反馈网络）的衰减系数。

• V外β 是 β 框的输出。

• V在– 五外β 是求和结点的输出。

到目前为止，衰减 （β） 表示为两个电阻器的比率。请记住，反馈网络可能比两个电阻器更复杂和复杂：使用二极管、电容器和电感器，甚至反馈回路中可能存在第二个运算放大器。在一些已发布的文章中，术语 V在– 五外• β称为误差电压 （E） 或总和电压 （Σ）。

该运算放大器具有有限（但非常大）的开环增益，并且 Σ 电压非常小。因此，非常小的 Σ 乘以（增加）非常大的 A老给我们 V外大多数情况下，电压正好是我们预期的。对于更高频率的信号（例如 10 kHz），A老明显小于直流或低频。这意味着 output 不再跟随 input （尽管有所增加），而是不会完全符合我们的预期 （即失真）。

要准确理解为什么会发生这种情况，我们需要进一步研究数学分析。我们将把这个问题留到我下一篇文章中讨论运算放大器。