复数与相量

在电气工程中，用于计算电阻、电流或直流电压叠加的数学工具是实数。

然而，在处理与频率相关的正弦电源和矢量时，实数并非我们唯一需要的数字类型。除了常规的实数外，复数被引入以解决涉及负数的平方根（√1）的复杂方程。

在电气工程中，这类数字被称为“虚数”。为了区分虚数与实数，工程领域常用字母“j”（即j算子）表示虚数。因此，将“j”置于实数前即可标记其为虚数运算。

虚数示例：j3、j12、j100等。复数则由两个不同但密切相关的部分组成——“实数部分”加“虚数部分”。

复数代表二维复平面（或称s平面）中的点，该平面由两条轴定义：水平轴称为“实轴”，垂直轴称为“虚轴”。复数的实部和虚部分别缩写为Re(z)和Im(z)。

由实数（有功分量）和虚数（无功分量）构成的复数，其加减运算规则与初等代数分析直流电路时完全相同。

虚数加减运算的数学规则与实数一致（例如j2+j4=j6）。唯一区别在于乘法——两个虚数相乘会得到负实数。实数也可视为虚部为零（标记为j0）的复数。

j算子的值严格等于√1，因此连续对“j”作乘法（j×j）将依次得到以下结果：1、j和+1。由于j算子通常用于表示矢量的逆时针旋转，每次连续的乘方（j²、j³等）会使矢量按固定角度90°逆时针旋转（如下图所示）。同理，若矢量乘法结果为j算子，则相位偏移为90°（即顺时针旋转）。

j算子的矢量旋转

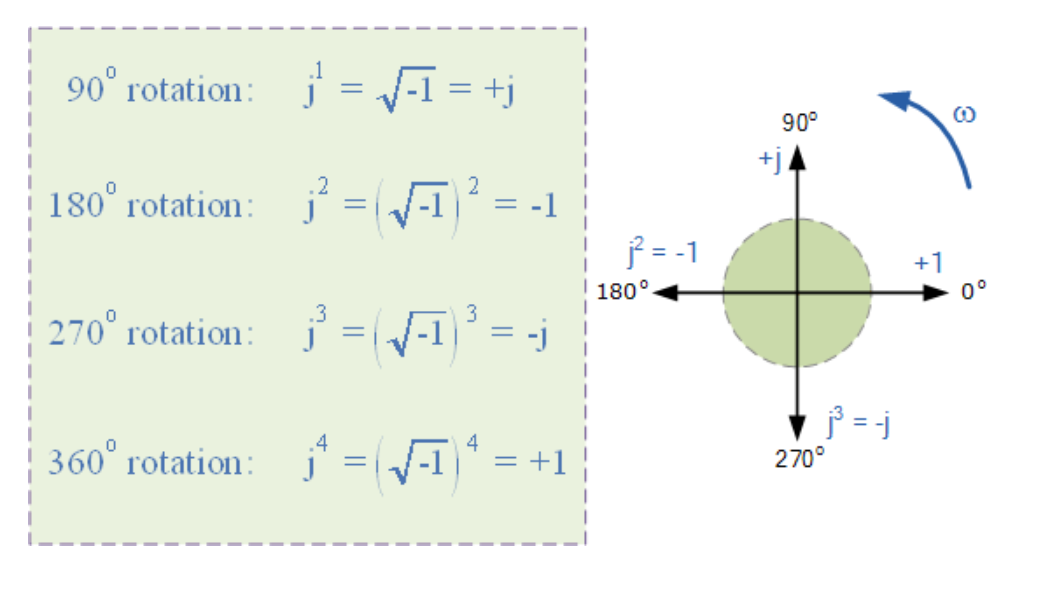
（图示：复数中j算子的矢量旋转）

因此，用j²乘以虚数会使矢量逆时针旋转180°，j³对应270°，j⁴则旋转360°回到原位。用j¹⁰或j³⁰相乘时，矢量将按相应角度逆时针旋转。每次旋转中，矢量幅值始终保持不变。

在电气工程中，复数可通过图形或数学多种方式表示。其中一种基于余弦和正弦法则的方法称为笛卡尔形式（直角坐标形式）。

复数的直角坐标表示

在关于相量的前篇教程中，我们了解到复数由实部和虚部构成，其通用形式为：

复数格式

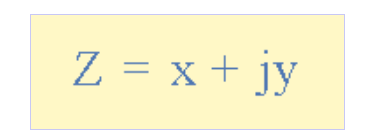
其中：

Z——代表矢量的复数

x——实部（有功分量）

y——虚部（无功分量）

j——定义为√1

在直角坐标形式中，复数可表示为复平面（s平面）上的一个点。例如Z=6+j4对应的坐标点为：实轴6，虚轴4（如下图所示）。

复数的复平面表示

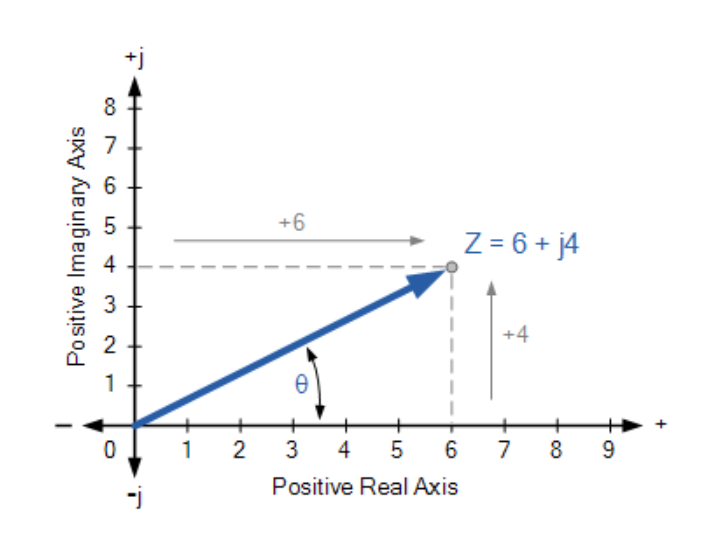
（图示：复数在s平面中的表示）

由于直角坐标形式中复数的实部和虚部均可正可负，因此实轴和虚轴均需双向延伸。这将形成包含四个象限的复平面，称为阿冈图（如下图所示）。

四象限阿冈图

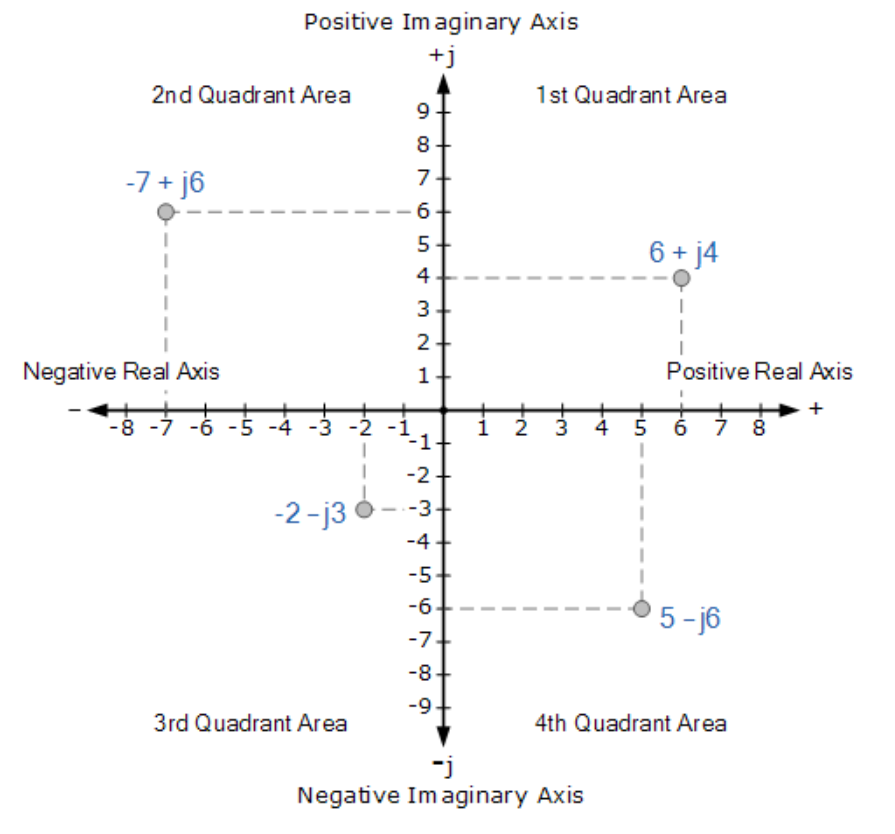
（图示：四象限阿冈图）

在阿冈图中：

水平轴右侧表示正实数，左侧表示负实数；

垂直轴上方表示正虚数，下方表示负虚数。

由此形成的二维复平面包含四个明确象限，标记为QI、QII、QIII和QIV。

上述阿冈图还可用于表示旋转相量——相量幅值为半径的点在复平面中每2π/ω秒完成一整圈旋转。

进一步扩展这一概念，可展示90°旋转时复数的极坐标与直角坐标定义：

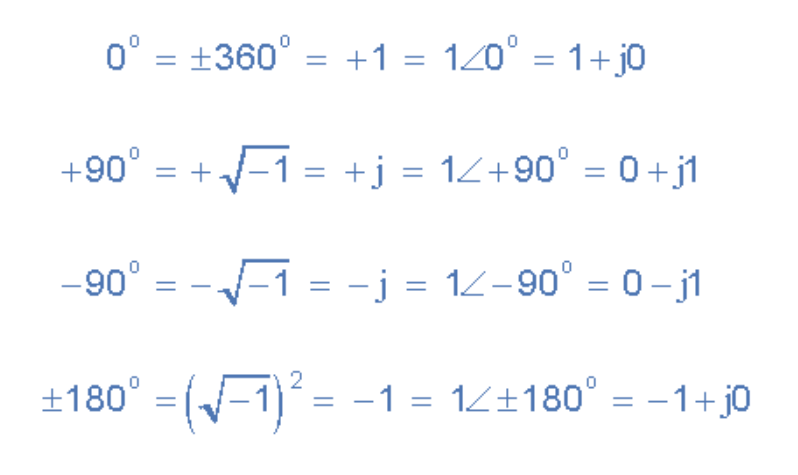
（图示：复数的极坐标与直角坐标定义）

复数也可能存在实部或虚部为零的情况（如Z=6+j0或Z=0+j4），此时点直接落在实轴或虚轴上。复数的角度可通过直角三角形三角函数计算，或从正实轴开始沿阿冈图逆时针测量。

角度划分规则：

0°至90°位于第一象限（I）；

90°至180°位于第二象限（II）；

180°至270°位于第三象限（III）；

270°至360°位于第四象限（IV）。

各象限角度可通过公式计算：

复数的加减运算

复数的加减可通过直角坐标形式的数学运算或图形化完成。加法运算时，先将实部相加得到和的实部，再将虚部相加得到和的虚部。以下以复数A和B为例演示该过程：

复数加减法示例

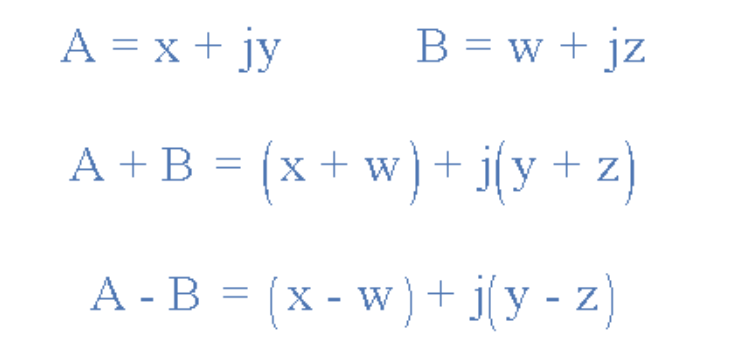
（图示：复数加减法运算）

复数示例1

定义两个矢量：A=4+j1，B=2+j3。分别以直角坐标形式（a+jb）和阿冈图求解两矢量的和与差。

数学加减法

加法：

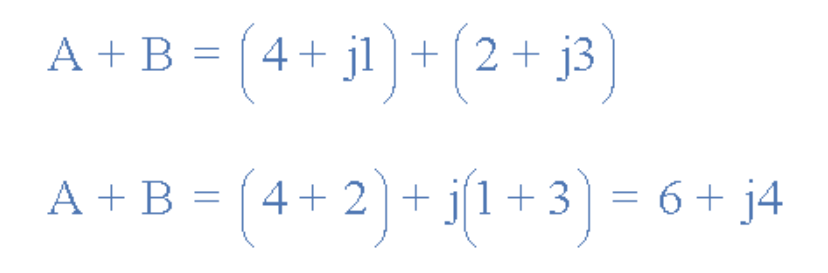
减法：

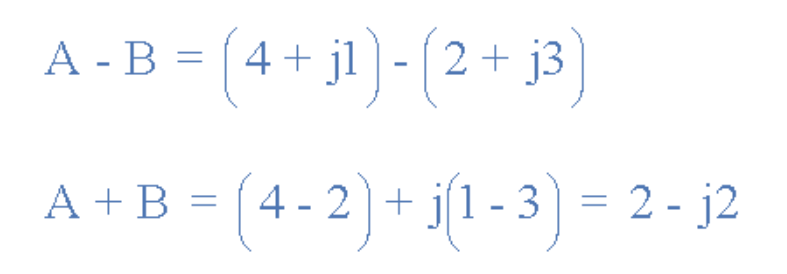
图形化加减法

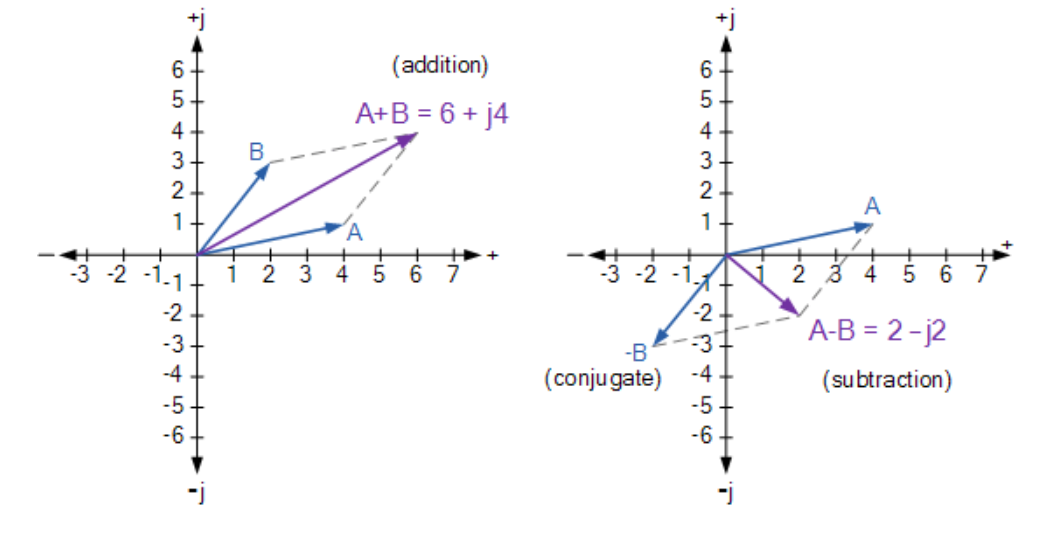
（图示：图形化加减法演示）

复数的乘除运算

直角坐标形式的复数乘法遵循与常规代数相似的规则，并增加j算子连续乘法的特殊规则（j²=1）。例如，将上述矢量A=4+j1与B=2+j3相乘结果如下：

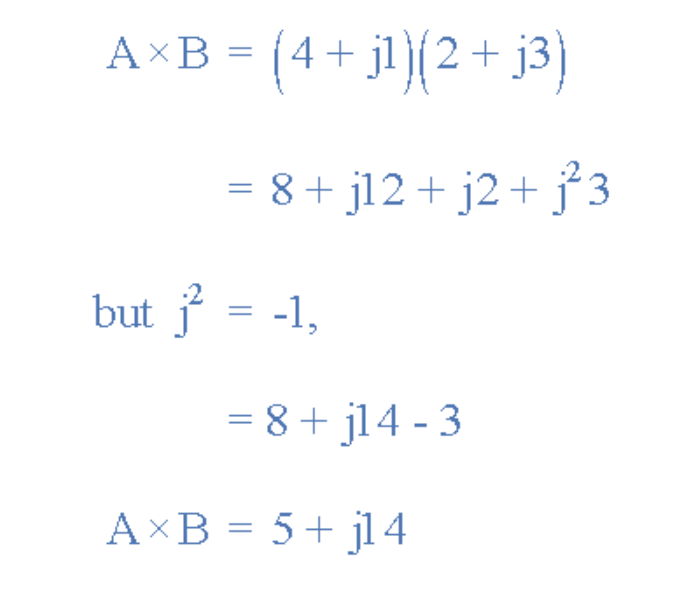
数学上，直角坐标形式的复数除法较为复杂，需要通过分母共轭函数将分母转换为实数（称为“有理化”）。因此复数除法建议采用极坐标形式求解（后续讨论）。不过，此处仍以直角坐标形式演示矢量A除以矢量B的过程：

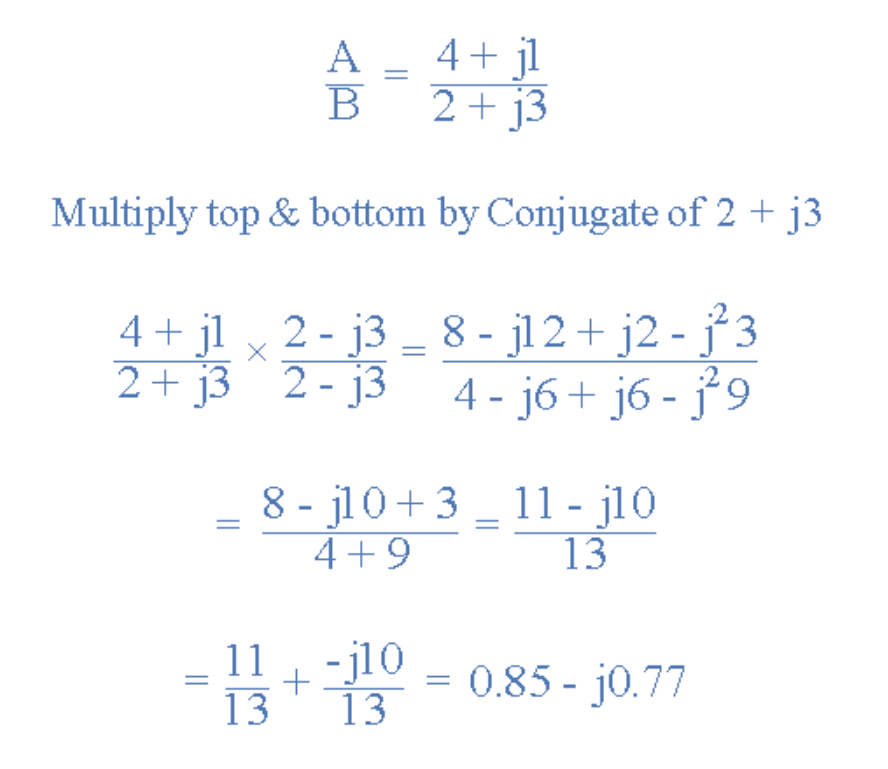
复数的共轭

复数的共轭（简称共轭）是指仅改变复数虚部的代数符号，而保持实部符号不变。复数的共轭记作 z 。例如：

z = 6 + j4的共轭为 z = 6 – j4

z = 6 – j4 的共轭是 z = 6 + j4

在阿冈图中，共轭复数与原复数在实轴上的位置相同，但在虚轴上的位置相反。因此，共轭复数可视为原复数在实轴上的镜像反射。下图展示了复数(6+j4)及其共轭在复平面中的表示：

共轭复数图示

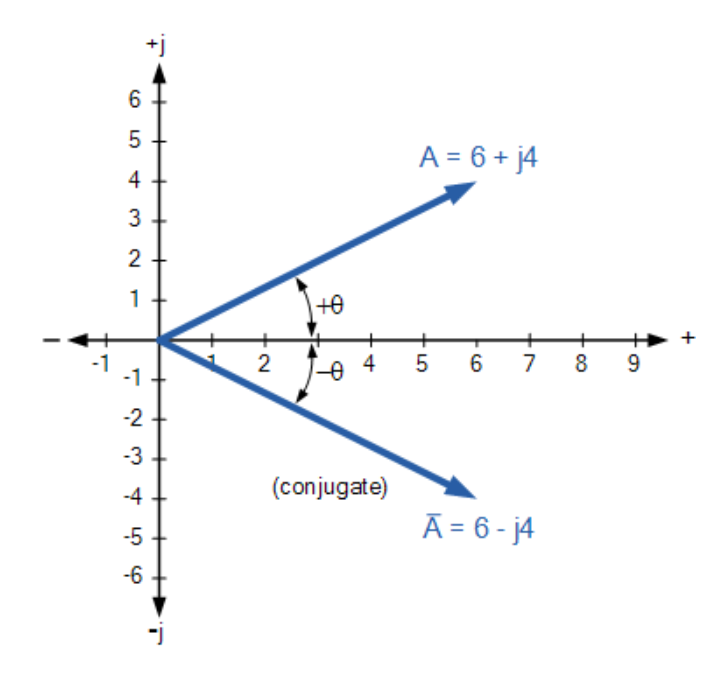
（图示：复数及其共轭在复平面中的位置）

正如我们上面看到的，复数及其复共轭之和将始终是一个实数。然后，将复数及其共轭相加仅给出实数或有功分量的结果，而它们的减法仅给出虚数或无功分量。复数的共轭是电气工程中用于确定使用矩形形式的交流电路的视在功率的重要元素。

复数的极坐标形式

与直角坐标形式（用复平面中的点表示）不同，极坐标形式通过幅值和角度描述复数，表示为：

Z = A ∠±θ

其中：

Z：极坐标形式的复数

A ：矢量的幅值（模）

θ ：矢量的角度（幅角），可正可负

极坐标形式中，点的位置以“三角形”表示（如下图所示），其幅值和角度与直角坐标形式相同，可通过三角学和勾股定理计算：

极坐标形式的复数表示

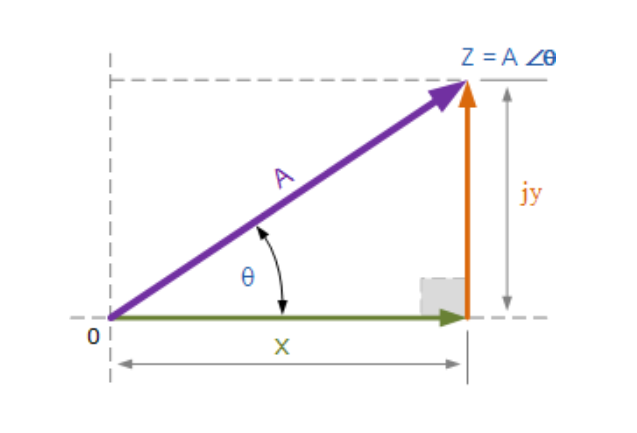
（图示：极坐标形式的复数）

幅值与角度的计算

幅值（模）：

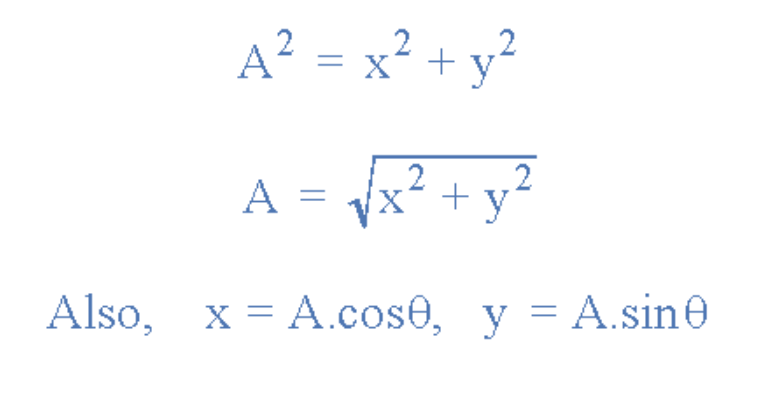
角度（幅角）：

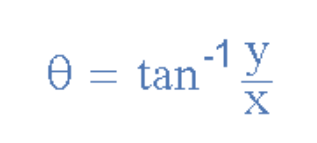
极坐标形式的共轭复数与原复数幅值相同，但角度符号相反。例如，6 ∠30o的共轭为6 ∠– 30o。

直角坐标与极坐标的转换

直角坐标形式与极坐标形式的相互转换

在直角坐标系中，我们可以用水平轴（实轴）和垂直轴（虚轴或j分量轴）的坐标来表示矢量。而在极坐标系中，这些实轴和虚轴被简化为"A∠θ"的形式。以前文示例为基础，两种坐标系之间的转换关系可定义如下：

极坐标转直角坐标（P→R）

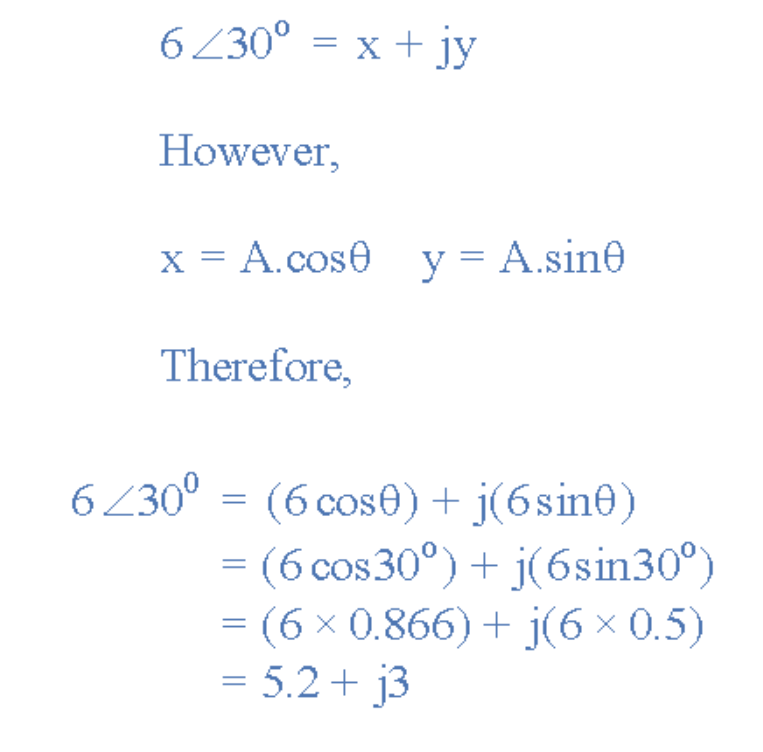
[插入复数转换公式图示]

我们同样可以进行逆向转换：

直角坐标转极坐标（R→P）

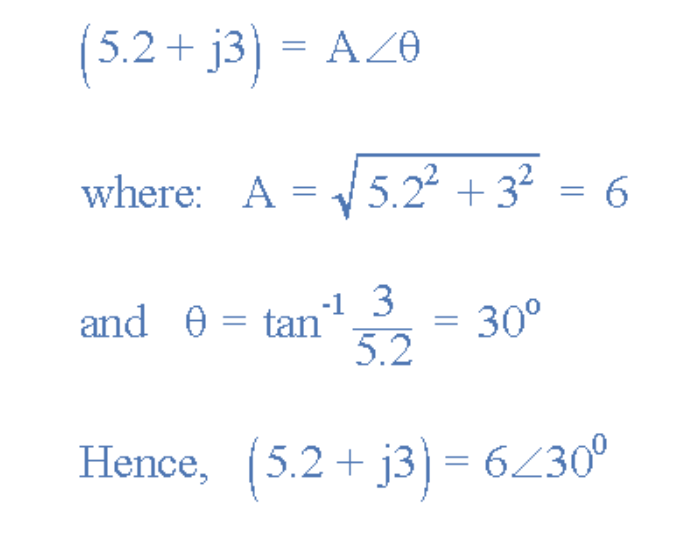
[插入复数转极坐标图示]

极坐标下的乘法与除法运算

虽然直角坐标形式最适合进行复数的加减运算（如前文所述），但极坐标形式在乘除运算中更具优势。进行极坐标矢量乘法运算时，需先对两个模量（幅值）进行乘积运算，再对其相位角进行求和。

极坐标乘法公式

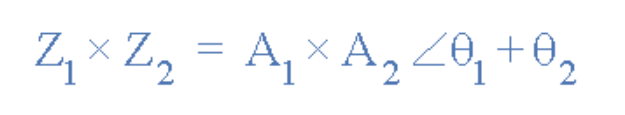
[插入极坐标乘法公式图示]

示例：6∠30°与8∠-45°的极坐标乘法运算结果为：

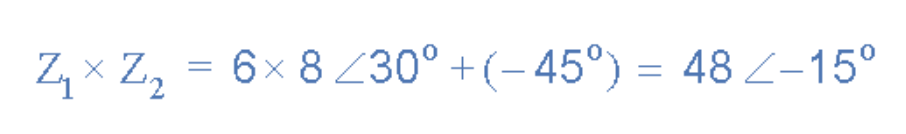
[插入极坐标乘法示例图示]

极坐标除法公式

同理，进行极坐标矢量除法时，需对两个模量作除法运算，再对其相位角作减法运算：

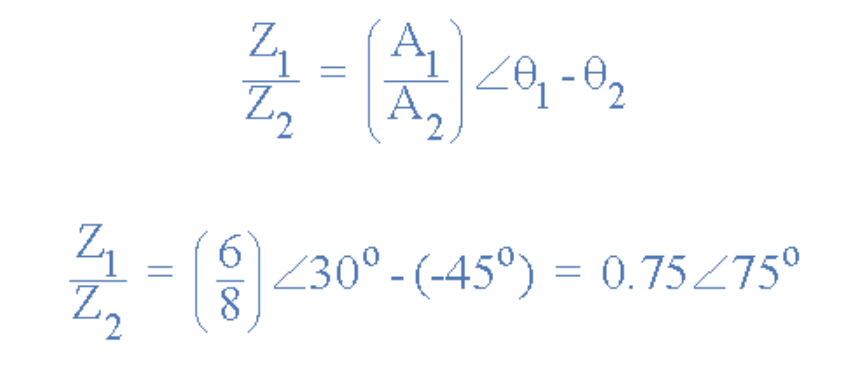
[插入极坐标除法公式图示]

[插入极坐标除法示例图示]

现代科学计算器已内置数学转换功能（详见说明书），可轻松实现直角坐标与极坐标的双向转换（R→P和P→R）。

复数的指数形式表示

截至目前，我们已探讨了复数的两种表示形式：直角坐标形式（a+jb）和极坐标形式（A∠±θ）。但还存在第三种表示方法——指数形式，其原理与极坐标形式类似，均对应正弦波的幅值和相位角，但采用自然对数底数e（e=2.718281...）来计算复数值。

指数形式通过直角三角形中的正弦（sin）和余弦（cos）三角函数来定义复平面中的旋转点。这种表示方法基于瑞士数学家莱昂哈德·欧拉提出的欧拉恒等式：

指数形式公式

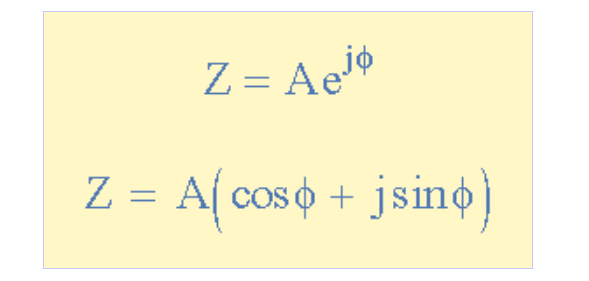
[插入复数指数形式旋转相量图图示]

那么欧拉恒等式可以用下面在复平面上的旋转相量图来表示。

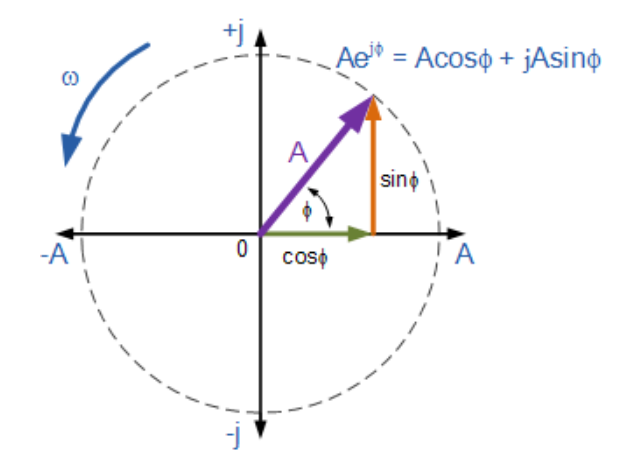
可以看出欧拉恒等式与极坐标形式高度相似，表明如Ae jθ这类幅值为1的数值也属于复数。我们不仅能将指数形式轻松转换为极坐标形式（例如：2e j30 = 2∠30, 10e j120 = 10∠120 ， -6e j90 = -6∠90），还能通过欧拉恒等式将指数形式转换为直角坐标形式。因此，复数在指数、极坐标和直角坐标三种形式间的转换关系为：

复数形式对照

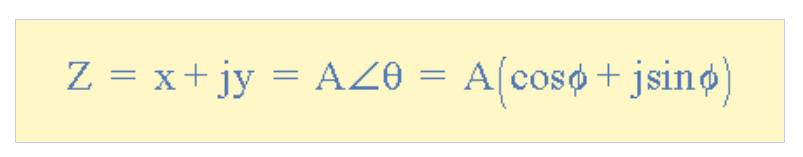
[插入复数形式关系图示]

相量表示法

前文已探讨了用复数表示旋转矢量或静态矢量的不同方法。相量表示法是通过构建单一复数来描述正弦波的幅值和相位角的过程。

相量表示法（或称相量变换）将正弦函数的实部 A(t) = Am cos(ωt ± Φ)从时域转换到复数域（即频域）。例如：

[插入指数形式复数示例图示]

（注：√2将最大幅值转换为有效值/均方根值，相位角以弧度ω表示）

复数知识总结

本节教程关于复数及其在电气工程中的应用总结如下：

1. 复数由实部和虚部两个独立部分组成

2. 虚数通过j算子与实数区分

3. 字母"j"前缀标识该数为复平面中的虚数

4. 根据定义，j算子j≡√-1

5. 虚数可像实数一样进行加减乘除运算

6. j×j的运算结果为j²=-1

7. 直角坐标形式用复平面上的点表示复数

8. 极坐标形式用带幅值和相位角的线段表示复数

9. 指数形式采用自然对数底数和对应角度表示复数

10. 复数的三种表示方法：

    Z=x+jy → 直角坐标形式

    Z=A∠Φ → 极坐标形式

    Z = A e jΦ→ 指数形式

11. 欧拉恒等式可实现指数形式到直角坐标形式的转换

在包括本篇在内的系列教程中，我们了解到相量可用于表示正弦波形，其幅值和相位角能以复数形式表示。我们还发现复数可采用直角坐标、极坐标或指数形式表示，并能进行各种代数运算，包括加减乘除。

在接下来关于交流串联电路相量关系的教程中，我们将探讨常见无源电路元件的阻抗特性，并通过绘制电流相量图和元件两端电压相量图进行分析，首先从交流电阻开始。