相位差与相移

相位差用于描述两个或多个交流量达到最大值或零值时在角度或弧度上的差异

相量(Phasor)是分析交流电路中各元件行为的有效工具，尤其适用于同频电路。两个相量相加的结果取决于它们的相对相位关系——由于相位差的存在，它们可能是"同相"或"异相"。

正弦波是一种沿时间轴水平呈现的交流量。作为时变量，正弦波在π/2时刻达到正最大值，在3π/2时刻达到负最大值，并在0、π和2π时刻通过零轴基准线。

但并非所有正弦波都会同时通过零轴点，相比另一个正弦波，它们可能向右或向左"偏移"一定量。例如比较电压波形与电流波形时，就会在两个正弦波之间产生角度偏移或相位差。任何在t=0时不经过零点的正弦波都存在相移。

正弦波的相位差(又称相移)是指波形沿水平零轴相对于某参考点偏移的角度Φ(希腊字母Phi)，单位可为度或弧度。换言之，相移是多个波形沿共同轴的横向差异，同频率正弦波之间可能存在相位差。

交流波的相位差Φ在一个完整周期内可在0到最大周期T之间变化，对应水平轴上Φ=0到2π(弧度)或Φ=0到360°的范围(取决于角度单位)。

相位差也可用时间偏移τ表示(单位为秒)，例如+10ms或-50μs，代表周期T的分数。但通常更习惯用角度值表示相位差。

因此，先前建立的正弦电压/电流瞬时值方程需加入相位角修正，新通用表达式为：

相位差方程

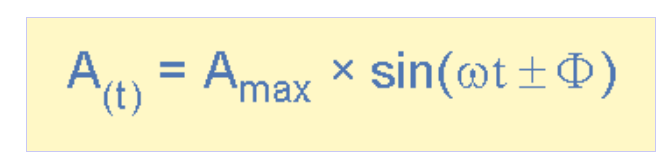
(此处插入相位角公式图)

其中：

Am-波形振幅

ωt-角频率(弧度/秒)

Φ-相位角(度或弧度)，表示波形相对于参考点的左右偏移

若正弦波的正斜率在t=0"之前"穿过水平轴，则波形左移(Φ>0)，相位角为正(+Φ)，形成超前相位角。这意味着波形比0°基准更早出现，对应相量逆时针旋转。

反之，若正斜率在t=0"之后"穿过水平轴，则波形右移(Φ<0)，相位角为负(-Φ)，形成滞后相位角。这意味着波形比0°基准更晚出现，对应相量顺时针旋转。两种情况如下图所示：

正弦波的相位关系

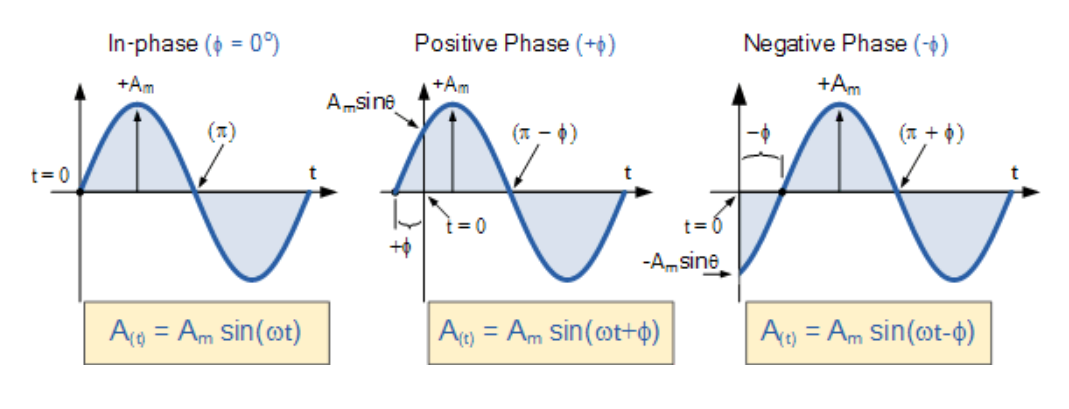
(此处插入正弦波相位关系图)

首先假设两个交流量(电压v和电流i)具有相同频率ƒ(Hz)。由于频率相同，角速度ω也必然相同。因此在任意时刻，电压v与电流i的相位相同。

在特定时间段内，旋转角度始终相同，故v与i的相位差为零(Φ=0)。由于电压v和电流i频率相同，它们会在同一时间达到正最大值、负最大值和零值(尽管幅值可能不同)。此时称这两个交流量"同相"。

两个同相正弦波

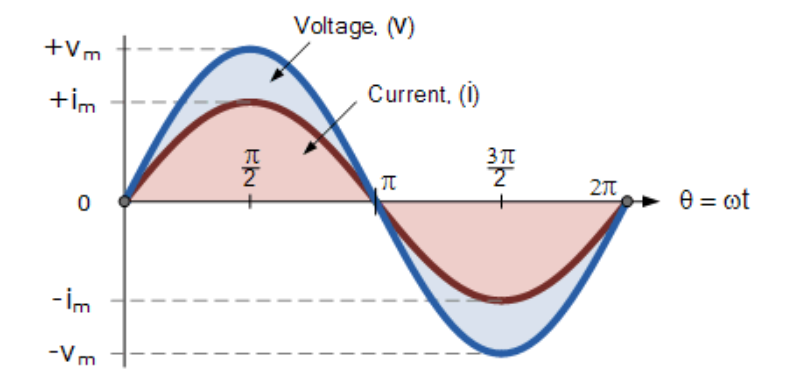
(此处插入同相正弦波图)

现假设电压v与电流i之间存在30°相位差(Φ=30°或π/6弧度)。由于两者旋转速度相同(即频率相同)，该相位差在所有时刻保持恒定。如下图所示，两波形间30°的相位差用Φ表示：

正弦波的相位差

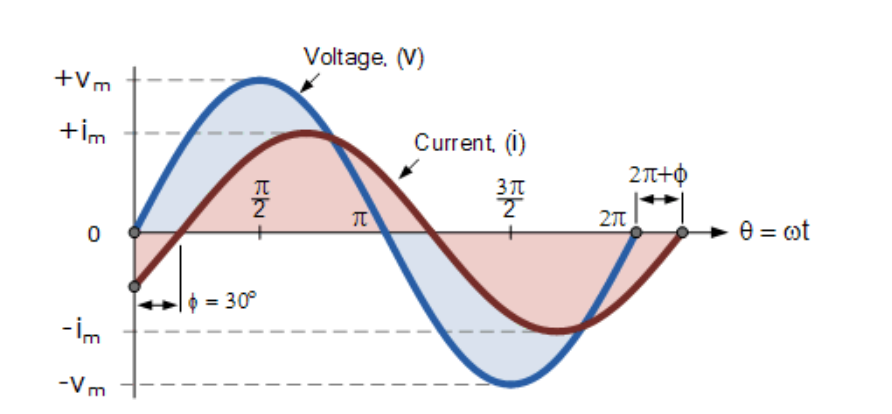
(此处插入两正弦波相位差图)

上方电压波形从水平参考轴零点开始，但同一时刻电流波形仍为负值，直到30°后才穿过参考轴。因此当电流波形穿过参考轴达到峰值和零值时，总比电压波形延迟，两者存在相位差。

由于两波形不再"同相"，而是存在Φ(本例为30°)的"异相"。可以说两波形现在有30°相位差。也可表述为电流波形比电压波形"滞后"相位角Φ。因此上例中的相位关系表达式为：

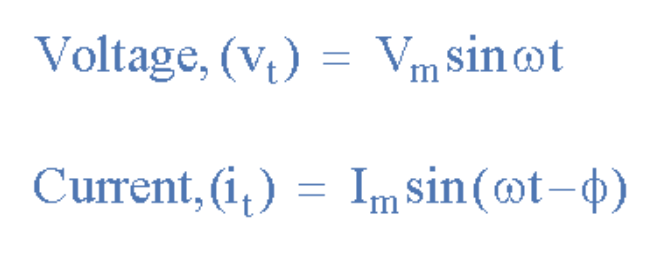
(此处插入滞后相位差公式图)

其中电流i滞后电压v相位角Φ

同理，若电流i先于电压v穿过参考轴达到峰值和零值，则称电流"超前"电压一定相位角。此时两波形存在超前相位差，表达式为：

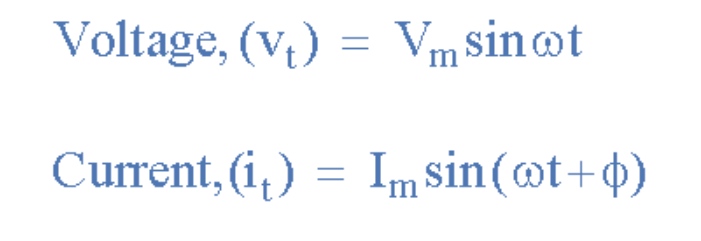
(此处插入超前相位差公式图)

其中电流i超前电压v相位角Φ

通过"超前"和"滞后"术语，可以描述同频率正弦波在相同参考轴上的相位关系。上例中两波形相位差30°，既可说i滞后v，也可说v超前i——取决于选择哪个作为参考。

两波形间的相位关系可通过测量它们沿水平零轴穿过时具有"相同斜率方向"(正或负)的位置来确定。在交流功率电路中，这种描述同一电路内电压与电流正弦波关系的能力至关重要，构成了交流电路分析的基础。

余弦波形

至此我们明白：当波形相对于另一正弦波向右或左"偏移"时，表达式变为Amsin(ωt±Φ)。但若某波形在参考波形之前90°(π/2弧度)以正斜率穿过零轴，则称为余弦波，其表达式为：

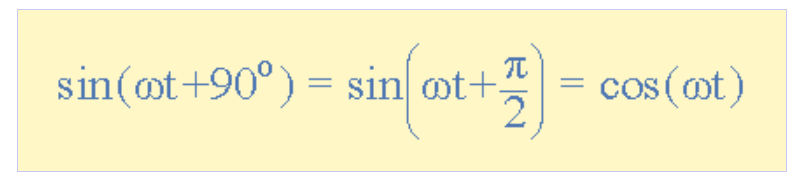
(此处插入余弦表达式图)

余弦波(简称"cos")在电气工程中与正弦波同等重要。余弦波与正弦波具有相同形状(均为正弦函数)，但超前了+90°(即1/4周期)。

正弦波与余弦波的区别

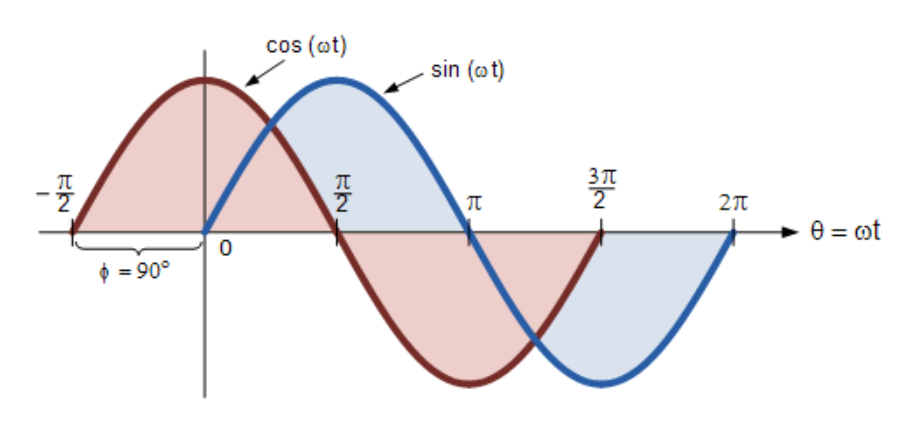
(此处插入相位差对比图)

也可认为正弦波是向另一方向偏移-90°的余弦波。无论哪种情况，处理含角度的正弦波或余弦波时，以下规则始终适用：

正弦波与余弦波的关系

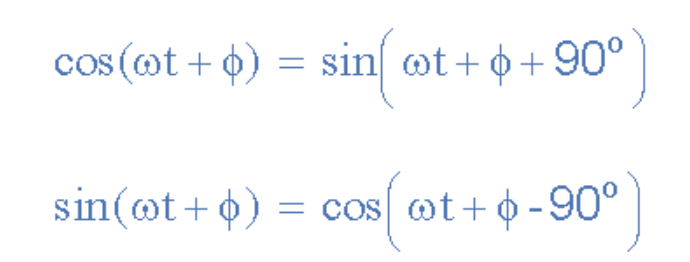
(此处插入正弦余弦关系图)

比较两个正弦波时，通常将其关系表示为具有正幅值的正弦或余弦函数，这可通过以下数学恒等式实现：

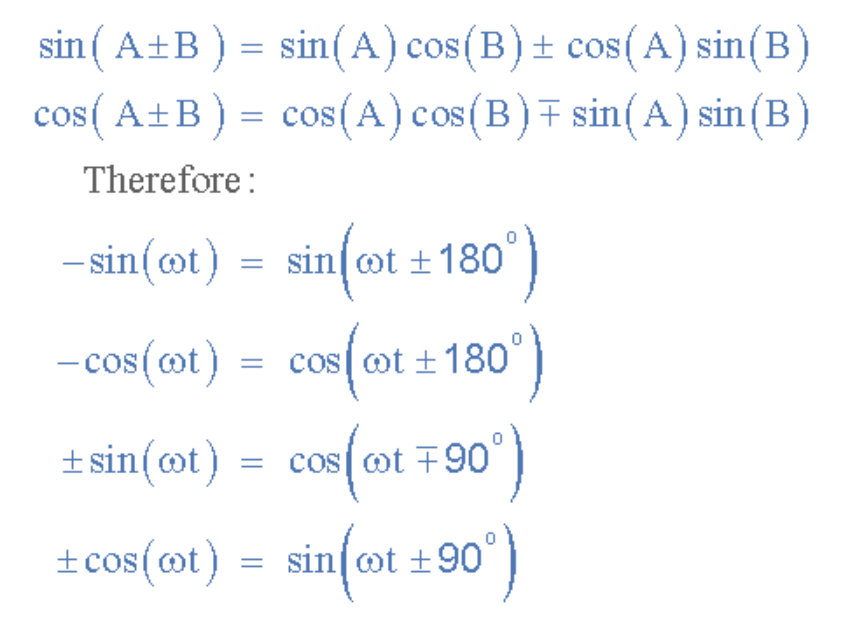
(此处插入正弦余弦恒等式图)

利用这些关系式，我们可以将任意含角度差或相位差的正弦波形转换为余弦波形，反之亦然。

在下一篇关于相量的教程中，我们将采用图形化方法，通过单相交流量的相量表示及相量代数运算，来直观比较两个正弦波的相位差。