正弦波形

正弦交流波形是随时间变化的周期性波形，其参数包括电压和频率

正弦波形是一种周期性波形，其形状可通过三角学中的正弦或余弦函数绘制。由正弦波形供电的电路，其极性每周期变化一次，通常称为"交流"(AC)电压和电流源。

当电流流过导线或导体时，会在导线周围形成环形磁场，其强度与电流值相关。若使单根导线在静止磁场中移动或旋转，由于导体切割磁力线，导体内部会感应出"电动势"(EMF)。

由此可见，电与磁之间存在关联性，正如迈克尔·法拉第发现的"电磁感应"效应。这一基本原理被电机和发电机用来产生我们日常使用的正弦交流电。

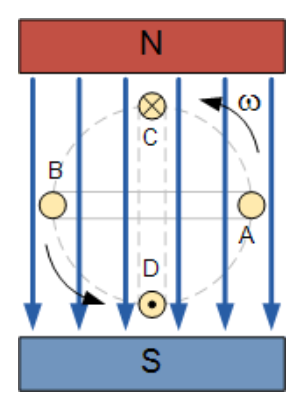
旋转线圈

在电磁感应教程中我们提到，当单根导线切割永磁场的磁力线时，内部会感应出电动势。

然而，当旋转导体在A、B两点位置与磁场平行移动时，没有切割任何磁力线，因此不会产生感应电动势。当导体在C、D两点位置与磁场垂直移动时，切割的磁力线数量最多，产生的感应电动势也最大。

此外，导体在A、C两点之间(0-90°)以不同角度切割磁场时，感应电动势的大小将介于零到最大值之间。因此，导体中的感应电动势大小取决于导体与磁力线的夹角以及磁场强度。

交流发电机利用法拉第电磁感应原理，将旋转等机械能转化为电能——即正弦波形。简单发电机由一对永磁体组成，在南北极之间形成固定磁场。磁场内放置一个可绕固定轴旋转的矩形导线环，使其能以不同角度切割磁力线，如下图所示。

基础单线圈交流发电机

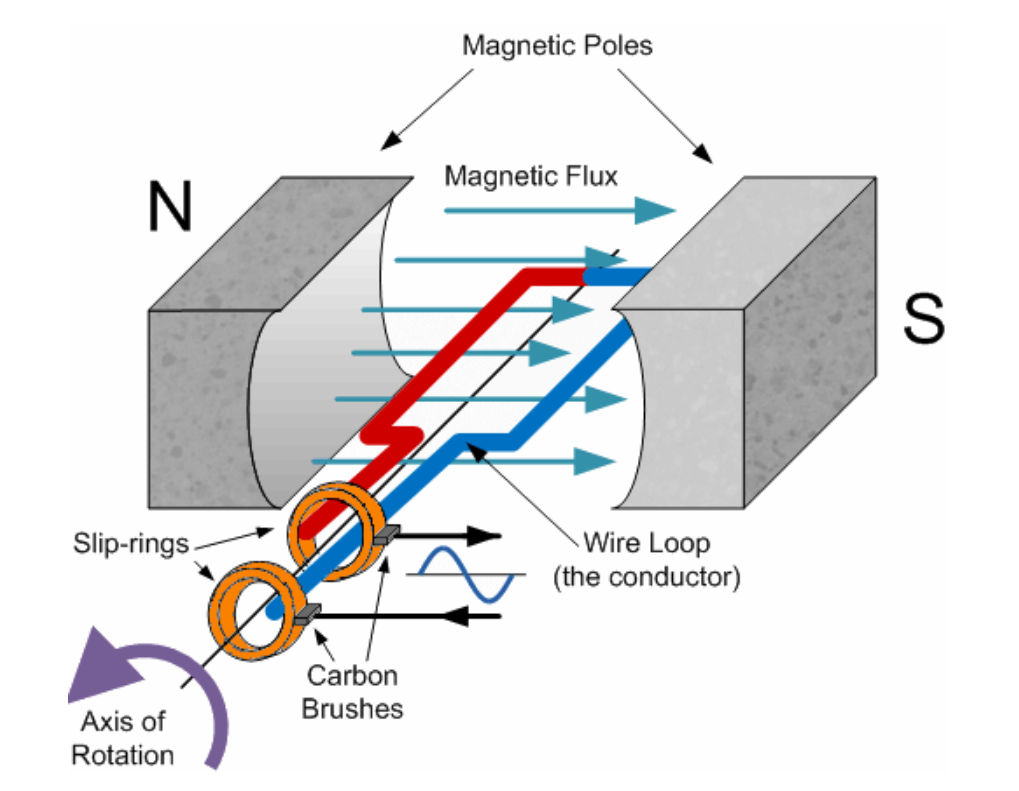
(此处插入交流发电机示意图)

当线圈沿垂直于磁场的中心轴逆时针旋转时，导线环以不同角度切割南北极之间的磁力线。任意时刻线圈中的感应电动势大小与导线环的旋转角度成正比。

随着导线环旋转，电子沿环向一个方向流动。当导线环旋转超过180°点反向切割磁力线时，电子流动方向随之改变，从而改变感应电压的极性。

由此可见，线圈每完成360°完整旋转，就产生一个完整周期的正弦波形。线圈在磁场中旋转时，通过碳刷和滑环将感应电流导出。

线圈切割磁力线产生的电动势大小由以下三个因素决定：

1.转速——线圈在磁场中的旋转速度

2.强度——磁场的强度

3.长度——切割磁场的线圈或导体长度

我们知道电源频率是指每秒出现的周期数，单位为赫兹(Hz)。如上所示，线圈在包含南北极的磁场中每旋转一圈产生一个感应电动势周期，若保持恒定转速，则每秒产生固定数量的周期，从而形成恒定频率。因此提高线圈转速将增加频率。故频率与转速成正比(ƒ∝Ν)，其中Ν=转/分钟(r.p.m)。

此外，我们简单的单线圈发电机仅有两个磁极(一北极一南极)，即一对磁极。若增加磁极数量至四个(两北极两南极)，则在相同转速下每转可产生两个周期。因此频率与磁极对数成正比(ƒ∝P)，其中P="磁极对数"。

综上可得交流发电机的频率输出公式：

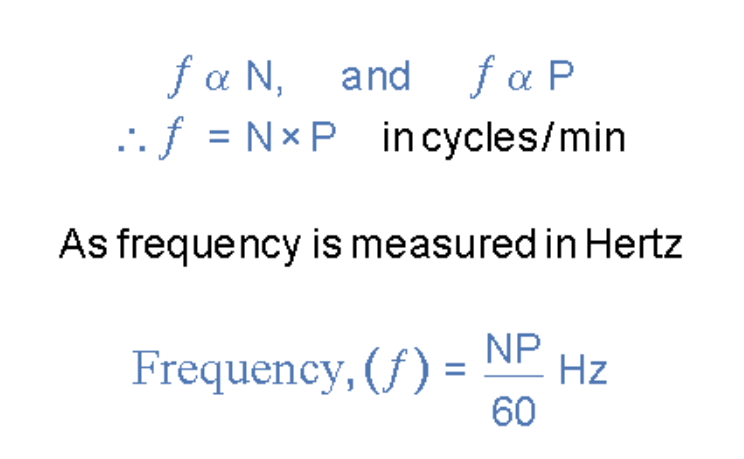
其中：Ν为转速(r.p.m)，P为"磁极对数"，60用于转换为秒。

瞬时电压

线圈中任意时刻的感应电动势取决于切割磁力线的速率，即与发电装置的旋转角度θ相关。由于交流波形持续变化其幅值，每个瞬间的波形值都不相同。

例如，1ms时刻的值与1.2ms时刻的值就不同。这些值统称为瞬时值(Vi)。瞬时波形值及其方向随线圈在磁场中的位置而变化，如下图所示。

线圈在磁场中的位移

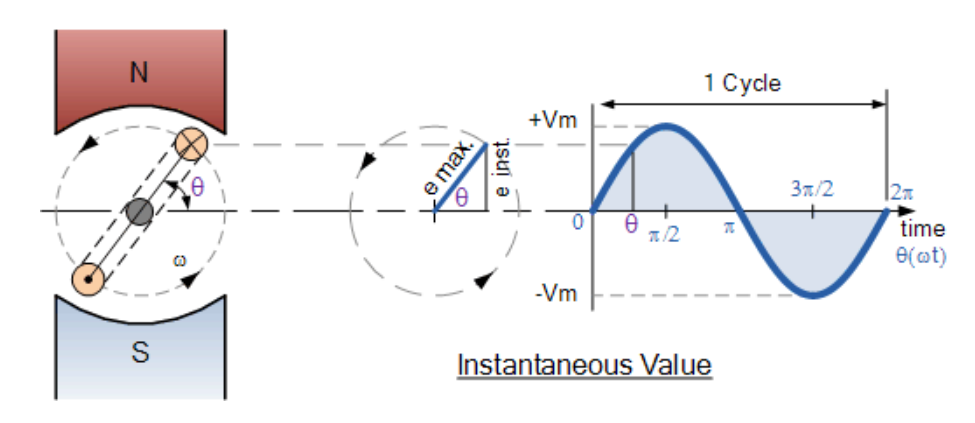
(此处插入线圈位移示意图)

正弦波形的瞬时值计算公式为："瞬时值=最大值×sinθ"，通用公式表示为：

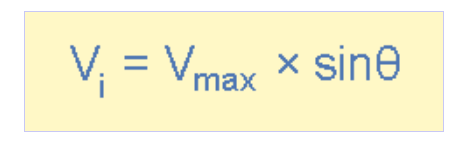
其中Vmax为线圈中感应的最大电压，θ=ωt表示线圈随时间变化的旋转角度。

若已知波形峰值，通过上述公式可计算出波形各点的瞬时值。将这些值绘制在坐标纸上，即可构建出正弦波形。

为简化计算，我们按每45°旋转角取一个瞬时值(共8个点)，并假设最大电压Vmax=100V。若采用更小间隔(如每30°取12个点或每10°取36个点)绘制，得到的正弦波形会更精确。

正弦波形构建

(此处插入正弦波形图)

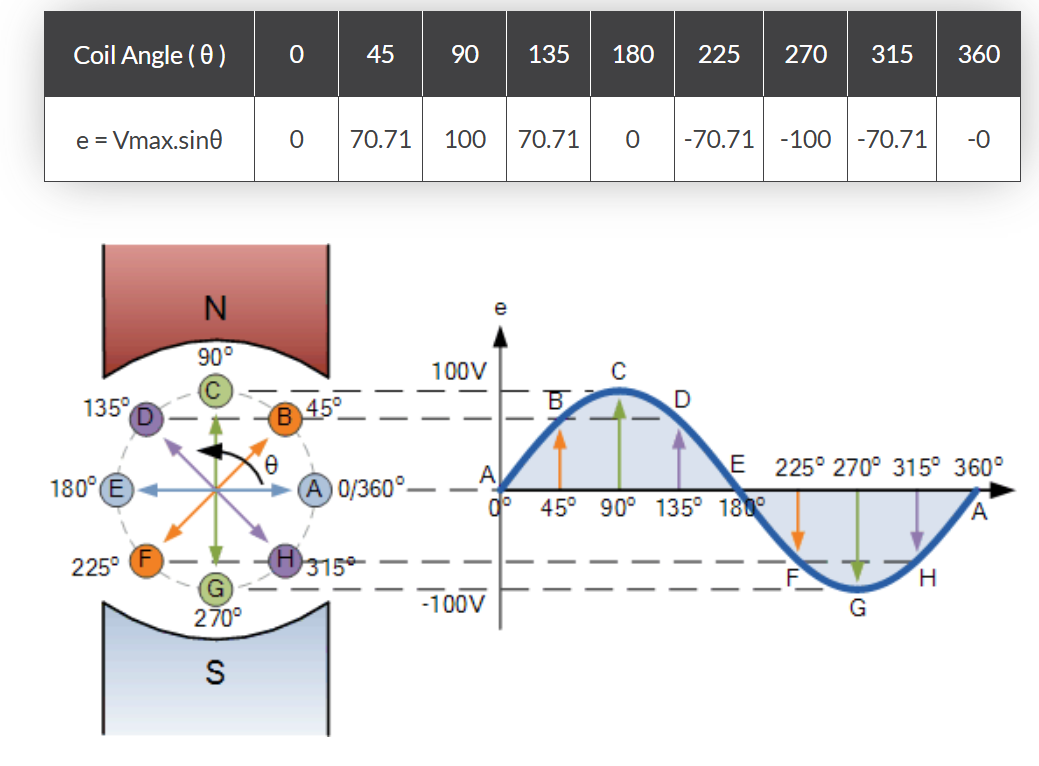
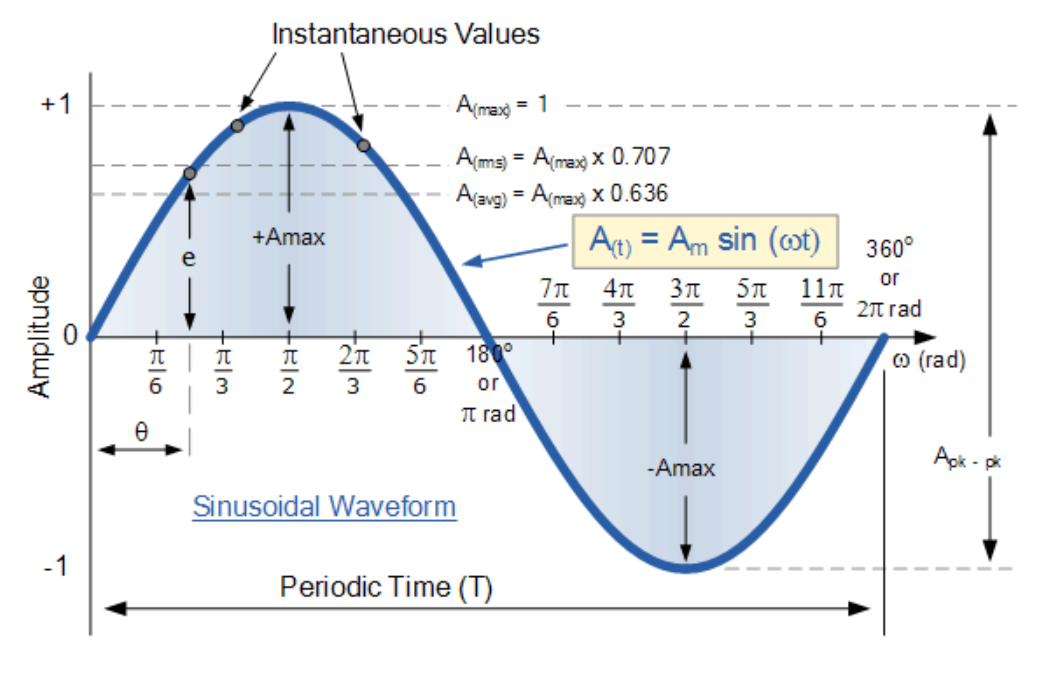
通过将0°-360°旋转位置投影到波形纵坐标上获得各点。当导线环或线圈完成360°完整旋转时，即产生一个完整波形。

从正弦波形图可见：当θ=0°、180°或360°时，因切割的磁力线最少，感应电动势为零；当θ=90°和270°时，因切割的磁力线最多，感应电动势达到峰值。

因此正弦波形在90°处有正峰值，270°处有负峰值。B、D、F、H各点产生的电动势符合公式：e=Vmax.sinθ。

这种由简单单环发电机产生的波形因其形状符合正弦函数而被称为正弦波。数学上表示为x(t)=Amax.sinθ。

处理时域中的正弦波(尤其是电流相关正弦波)时，横轴单位可采用时间、角度或弧度。电气工程中更常用弧度而非角度作为水平轴的角度量单位，例如ω=100rad/s或500rad/s。

弧度

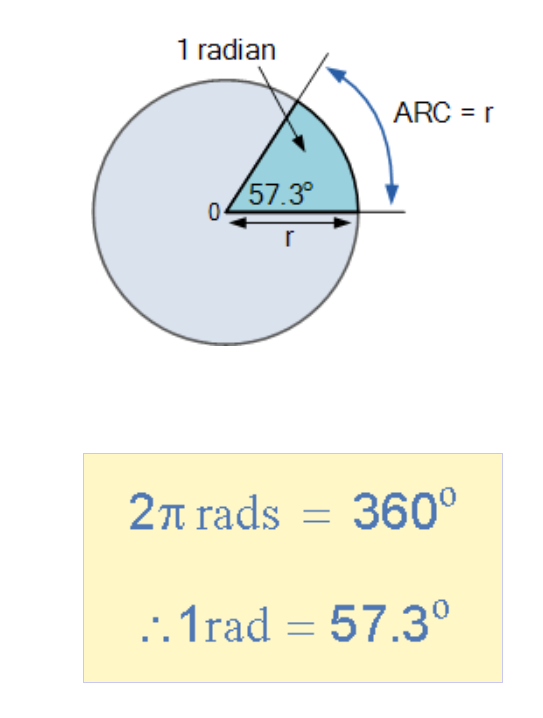
弧度(rad)的数学定义是：圆的象限弧长等于该圆半径(r)时的圆心角。由于圆周长为2π×半径，故360°圆周包含2π弧度。

换言之，弧度是角度测量单位，1弧度(r)对应的弧长在圆周上恰好出现2π(约6.284)次。因此1弧度=360°/2π=57.3°。在电气工程中弧度使用非常普遍，需牢记以下公式：

弧度定义

(此处插入弧度定义图示)

使用弧度作为正弦波形的测量单位时，360°完整周期对应2π弧度，半个正弦波形对应1π弧度(即π)。已知π≈3.142，因此正弦波形的角度与弧度转换关系为：

角度与弧度关系

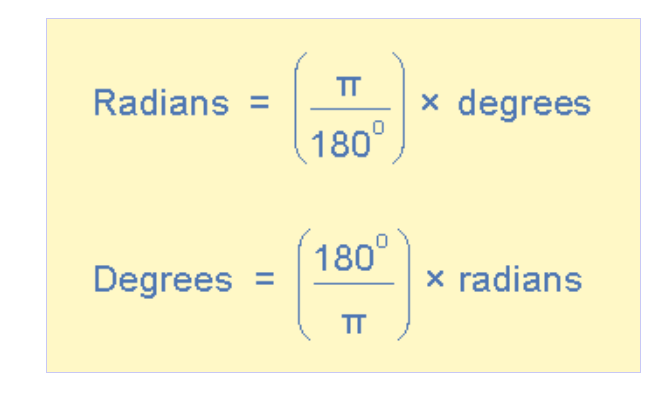
应用这两个公式可得波形各点对应值：

(此处插入正弦波形弧度对应图)

常见正弦分析中角度与弧度的换算关系如下表：

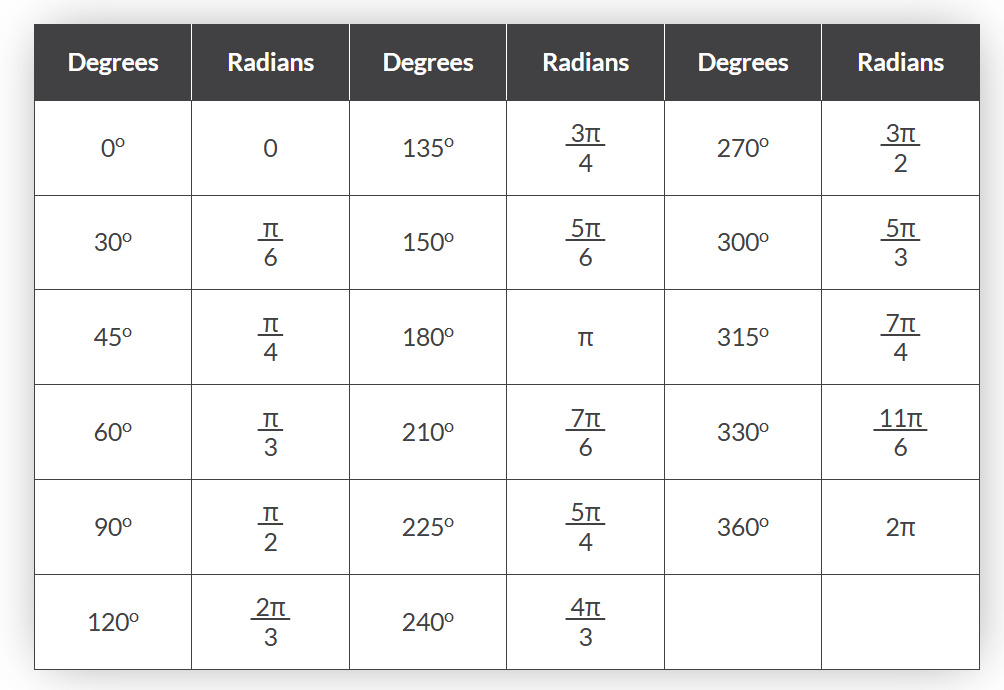
角度与弧度对照表

发电机绕中心轴的旋转速度决定了正弦波的频率。当波形频率为ƒ赫兹(Hz)或周/秒时，波形还具有角频率ω(单位：弧度/秒)。正弦波的角速度公式为：

在英国，电网的角速度或角频率为：

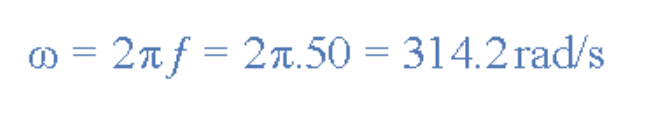
在美国，因电网频率为60Hz，故为：377rad/s

至此我们明白：发电机绕中心轴的旋转速度决定了正弦波的频率(即角速度ω)。同时还应知道，完成一整圈旋转所需时间等于正弦波的周期(T)。

由于频率与周期成反比(ƒ=1/T)，可将频率量替换为周期量，得到：

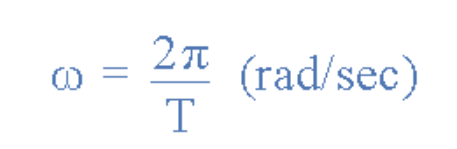
该式表明：正弦波的周期越短，角速度必须越大。同理，频率越高，角速度也越高。

正弦波形示例1

已知正弦波形定义为：Vm=169.8sin(377t)伏特。计算该波形的：

1.RMS电压

2.频率

3.6毫秒(6ms)时的瞬时电压值(Vi)

由正弦波通用表达式：

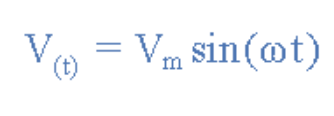
与给定表达式Vm=169.8sin(377t)对比可知：

峰值电压Vmax=169.8V

RMS电压计算为：

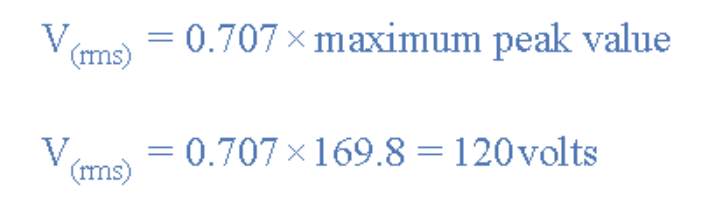
已知角速度ω=377rad/s，由2πƒ=377得频率：

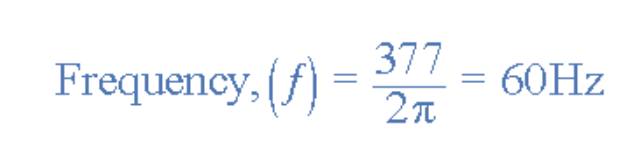
6ms时的瞬时电压值：

注：t=6ms时的角速度以弧度表示。如需转换为角度值计算瞬时电压，转换公式为：

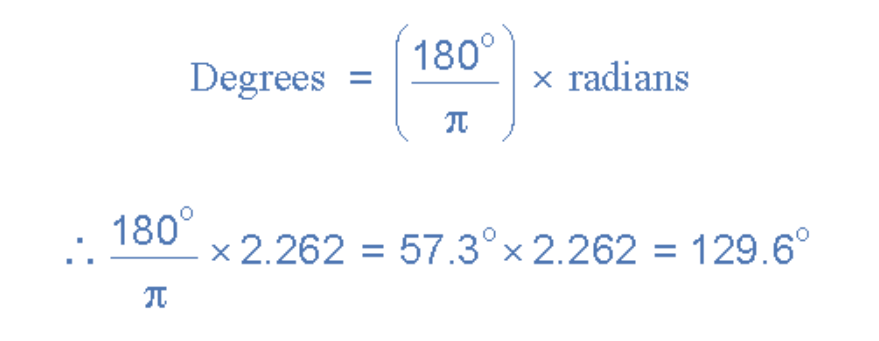
因此正弦波分析计算的通用格式如下：

(此处插入正弦波分析通用格式图示)

在下一篇关于相位差的教程中，我们将探讨两个同频率正弦波之间的关系，它们以不同时间间隔通过水平零轴。