利用ZY-Smith图设计二元匹配网络

了解导抗史密斯圆图（ZY-Smith chart）、添加串联和并联元件的效果、阻抗匹配以及寻找二元匹配网络。

在本系列的前面，我们讨论了如何分别使用阻抗史密斯圆图和导纳史密斯圆图方便地分析串联和并联电路。当处理并联和串联元件时，我们可以使用一个包括阻抗和导纳图的图表。同时具有阻抗和导纳轮廓的史密斯圆图被称为导抗史密斯圆图（或ZY-Smith图）。史密斯圆图是电气工程师菲利普·哈格·史密斯的发明。

ZY-Smith图表

导抗史密斯圆图如图1所示。

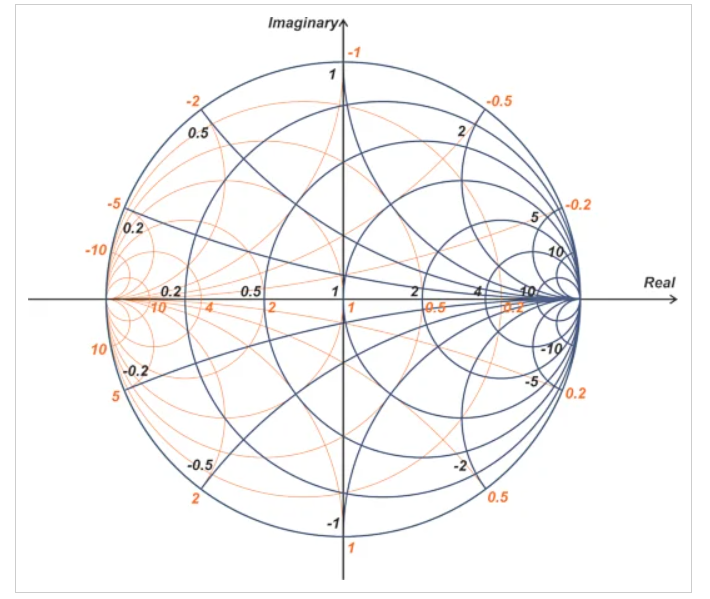
图1 示例导抗史密斯圆图

通过导抗史密斯圆图，我们可以很容易地找到给定阻抗的等效导纳，反之亦然。例如，假设归一化负载阻抗为z1=1+j1。我们可以在导抗史密斯圆图中定位z1，并直接从橙色曲线中读取其等效导纳。如下图2所示。

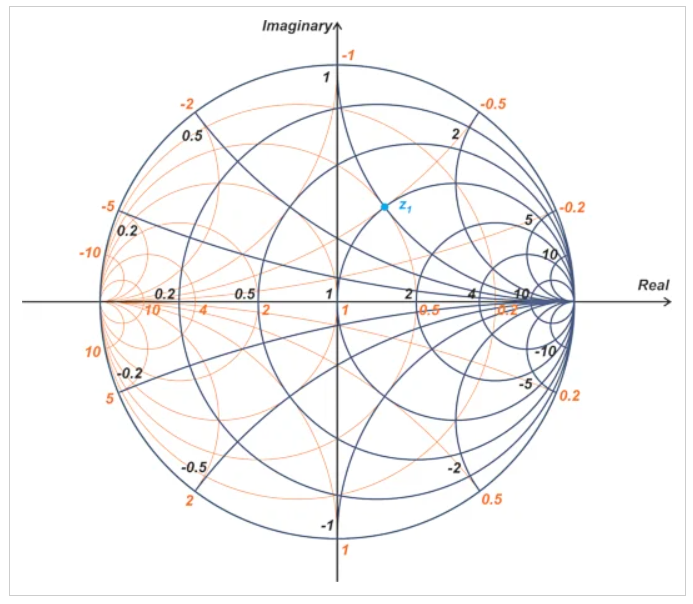
图2 使用导抗史密斯圆图的橙色曲线来找到z1的等效导纳

从上图中，我们发现等效导纳y1=0.5-j0.5。使用导抗图时，有一个主要的警告：请注意为您正在使用的曲线使用正确的数字。为了避免此类错误，请记住，大于r=1圆（或x=1弧）的圆（或弧）对应较小的数字。例如，在上图中，人们可能会怀疑穿过z1的橙色圆圈的电导值是2还是0.5。然而，由于这个圆大于r=1的圆，我们知道它的相关值是较小的一个（0.5）。

添加并联和串联组件的效果

下图（图3）显示了添加反应性成分如何改变我们在导抗图上的位置。

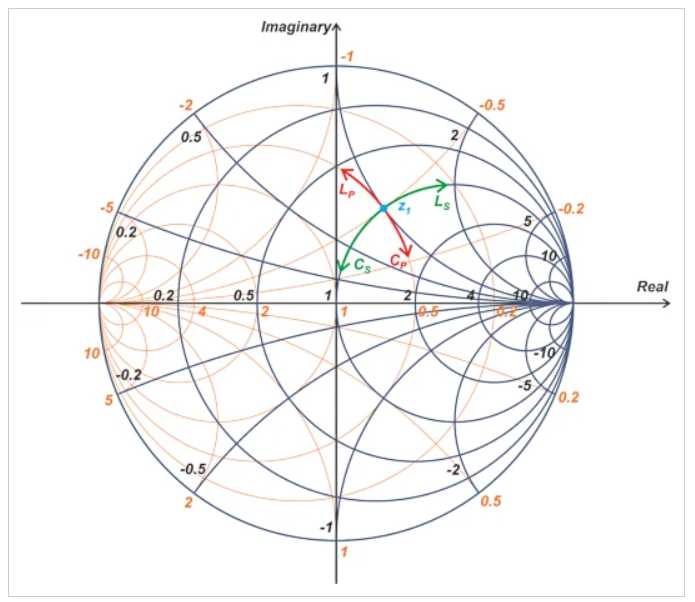
图3 带有电抗成分的导抗史密斯圆图

当添加串联电抗分量时，阻抗的实部是恒定的，因此，整体阻抗沿着恒定电阻圆移动。如果添加串联电感器LS，阻抗将沿顺时针方向移动。另一方面，对于串联电容器CS，运动方向为逆时针。

添加一个并联的电抗分量使我们在一个恒定的电导圆上移动。如果添加并联电感器LP，导纳将沿逆时针方向移动。对于并联电容器CP，其运动方向为顺时针。图4显示了添加串联电阻器RS或并联电阻器RP如何分别在恒定电抗或恒定电纳弧上移动我们。

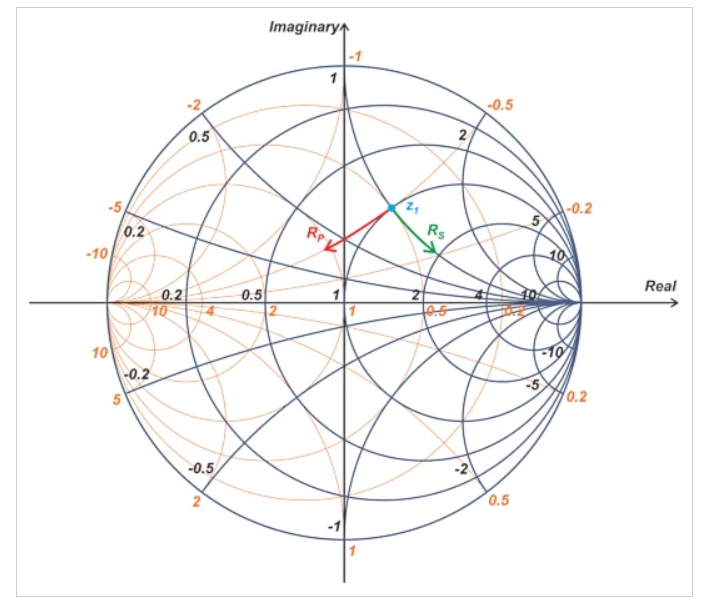
图4 阻抗史密斯圆图显示了添加串联或并联电阻器如何分别移动恒定电抗或恒定电纳弧

史密斯圆图的一个重要应用是阻抗匹配网络的设计，这将在本文的其余部分进行讨论。

阻抗匹配——将一个阻抗转换为另一个阻抗

阻抗变换或匹配是射频设计中的一个主要问题，以至于一些工程师认为射频设计就是阻抗匹配。出于各种原因，需要阻抗匹配。例如，为了减少电波反射，我们需要将负载阻抗与线路的特性阻抗相匹配。

寻找合适的二元匹配网络

使用导抗史密斯圆图，我们可以很容易地找到二元无损匹配网络。让我们通过一个例子来检验这一点。假设负载阻抗Z1=10+j10Ω与源阻抗Z2=50Ω相匹配。当阻抗归一化为Z0=50Ω时，阻抗归一化为z1=0.2+j0.2和z2=1（图5）。

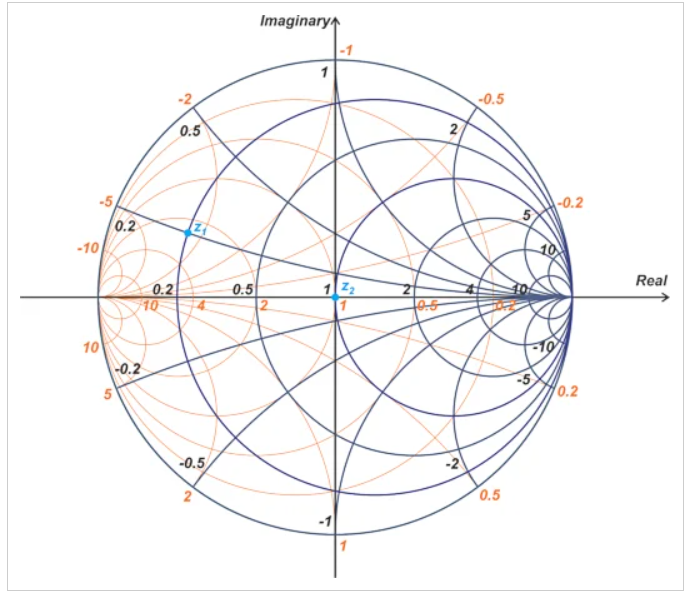
图5 导抗史密斯圆图显示了阻抗归一化

我们的目标是找到将z1转换为z2的二元无损匹配网络。由于我们正在设计一个无损匹配网络，因此无法添加电阻器。我们只能添加并联或串联的电抗元件。因此，匹配网络的设计涉及沿着穿过点z1和z2的恒定电阻或恒定电阻圆移动。图6显示了这些圆圈，为了清楚起见，删除了其他圆圈和圆弧。

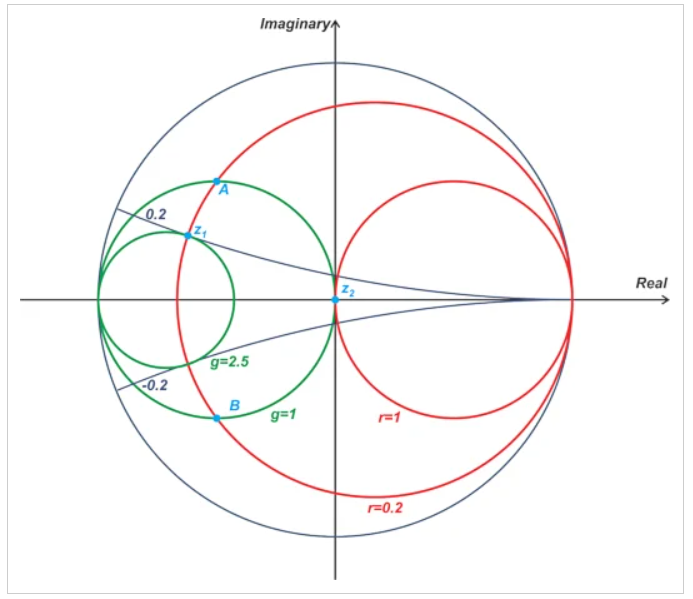
图6 显示匹配网络的恒定电阻或恒定电阻圆的示例图

由于有两个不同的圆穿过z1和z2，为了从z1移动到z2，我们需要使用一个穿过z1的圆和另一个穿过z2的圆。显然，这两个圆应该相交。在上述示例中，穿过z1的r=0.2恒定电阻圆和穿过z2的g=1恒定电阻圆满足这些条件。这两个圆在点A和B相交；因此，我们可以从z1到z2有两条不同的路径。下面的青色和橙色路径显示了这两种可能的选项（图7）。

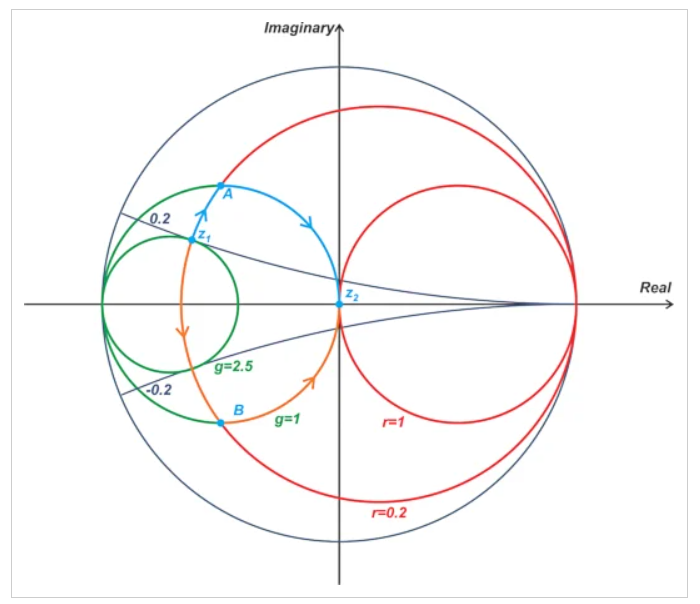
图7 显示交点A和B的图表

从z1到点A的运动对应于串联电感器，而从A到点z2的运动是由并联电容器产生的。因此，下面所示的两元件布置可用于将z1变换为z2。

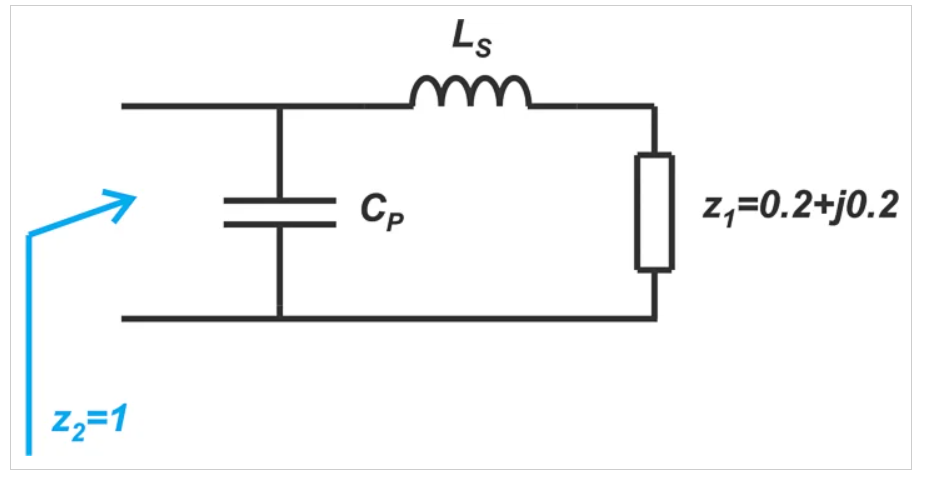
图8 示例二元排列

图7中的橙色路径对应于串联电容器（从z1到B）和并联电感器（从B到z2）。这为我们提供了另一个匹配网络，如图9所示。

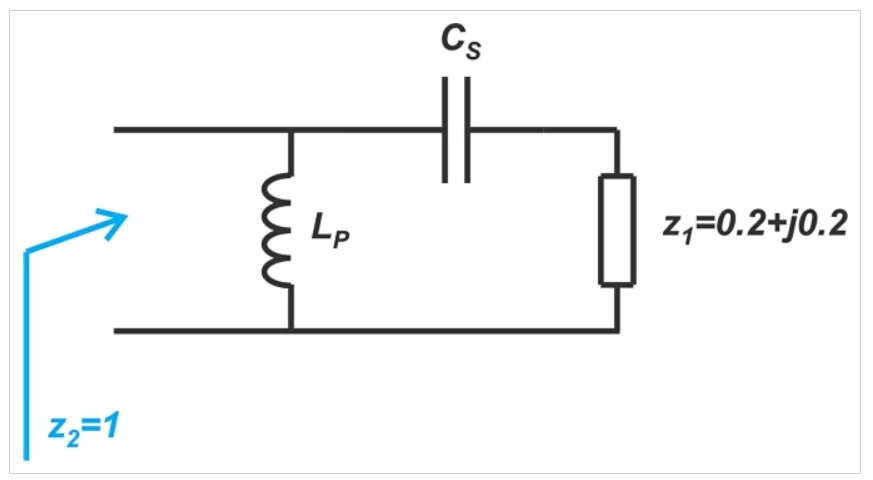
图9 匹配的网络图

查找匹配的网络组件值

为了找到上述匹配网络的分量值，我们需要知道点A和B的电抗和电纳。使用商业史密斯圆图，有足够数量的阻抗和导纳等值线来以合理的精度估计与图上任意点相关的值。图10中的史密斯圆图显示了A点和B点的电抗和电纳值。

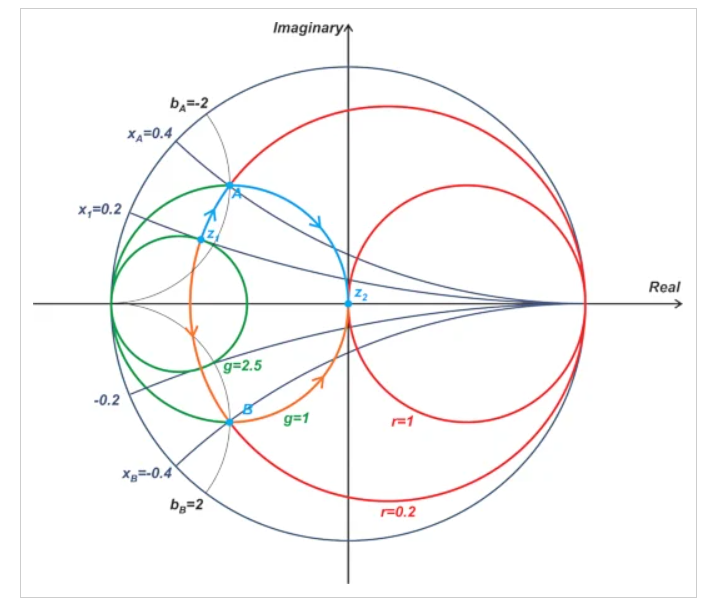
图10 史密斯圆图显示了A点和B点的电抗和电纳值

为了从z1移动到A，串联电感器的归一化电抗应为xA-x1=j0.2。假设工作频率为1 GHz，我们有：

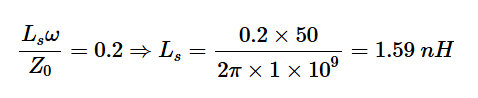
为了从点A到达z2，我们需要一个归一化电纳为j2的并联电容器。这反过来又将我们在点A处的初始电纳归零，并将我们移动到史密斯圆图的原点。1 GHz下的电容值为：

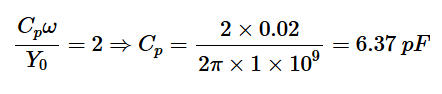
从青色路径获得的最终匹配网络如图11所示。

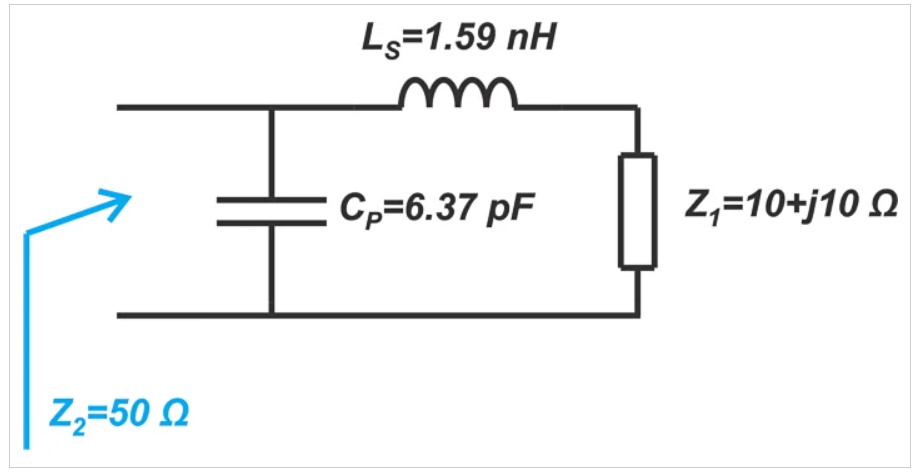
图11 匹配史密斯圆图中青色路径的网络图，我们在本文中一直在使用

如果你计算上述电路的输入阻抗，你会发现zin=49.96-j0.03Ω，这相当接近目标50Ω阻抗。同样，我们可以在图9中找到电路的元件值。在这种情况下，需要一个归一化电抗为xB-x1=-0.4j-0.2j=-0.6j的串联电容器从点z1移动到B。在1 GHz下，电容器值为：

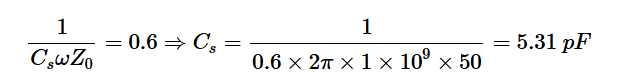
接下来，需要一个归一化电纳为-2的并联电感器从点B移动到史密斯圆图的原点。电感器值为：

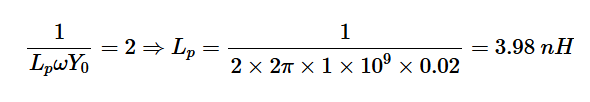
使用这些值，可以获得最终的匹配网络，如图12所示。

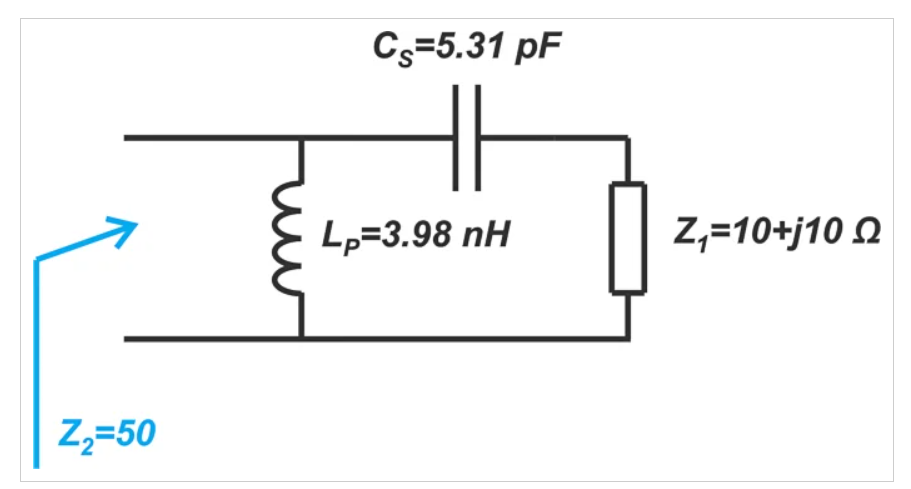
图12 最终的匹配网络图

我们可以再次找到输入阻抗来验证我们的计算。上述电路的输入阻抗为49.89-j0.11Ω，接近所需值。我们上面发现的匹配网络称为L-分段或L-网络。使用术语“L”是因为两个集总元件在电路图中形成了字母L。通过组合两个反应性组件，我们可以得到总共八个不同的L段匹配网络。在下一节中，我们将简要介绍其他一些L截面。

一个阻抗匹配问题的四个不同L截面

在图10所示的示例中，只有两个圆相互交叉。再举一个例子，考虑将图13所示的阻抗z3转换为史密斯圆图的原点。

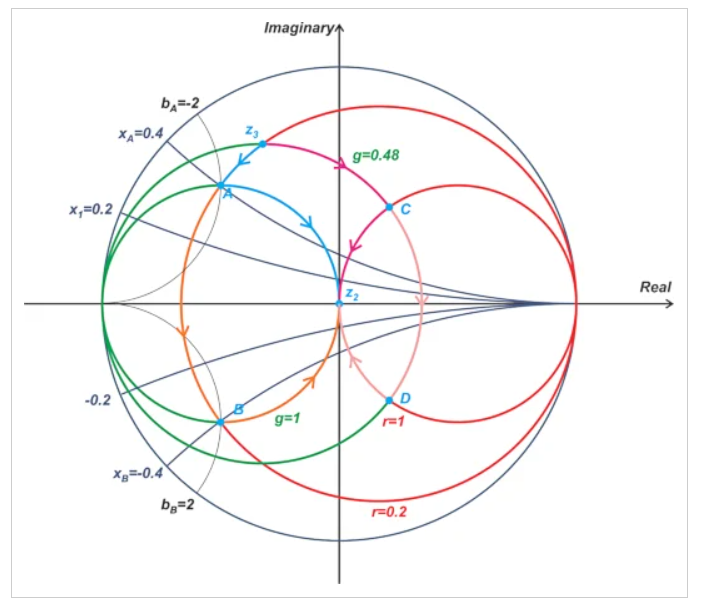
图13 阻抗z3的变换图

这个例子与前一个有一些相似之处。事实上，这两个例子中的三个圆是相同的（r=1、r=0.2和g=1的圆是一样的）。初始阻抗z3仅略微向上移动，使其恒定电阻圆（g=0.48）与目标阻抗的恒定电阻圆（r=1）相交。这将产生两个新的交点（点C和D）。由于这一变化，有两个新的阻抗匹配选项可用。图14显示了可用于此问题的四种不同的L截面。

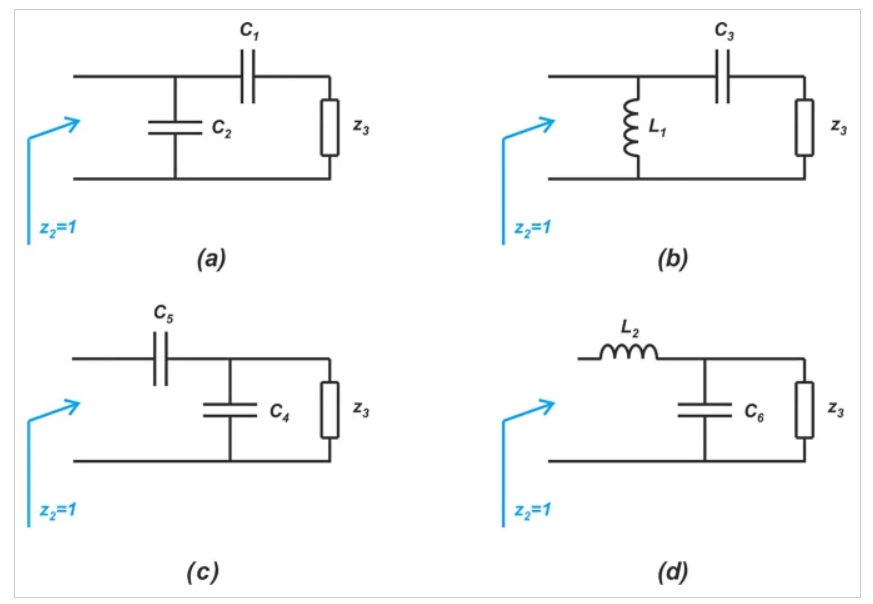
图14 四种不同的L剖面图

图14（a）、（b）、（c）和（d）中的L截面分别对应于穿过交点a、b、c和d的路径。可以看出，对于给定的匹配问题，我们可能有两个或四个不同的L型匹配解。在选择合适的匹配网络时，有几个不同的考虑因素。带宽、频率响应和易于实现是应该考虑的三个重要因素。在下一篇文章中，我们将更深入地探讨这个话题。