射频设计基础——传输线介绍

了解电压波及其与射频（RF）电路设计的一个重要基本概念：传输线的关系。

电路设计中的一个重要因素是电路元件和互连相对于被处理信号波长的物理尺寸。当信号频率足够低，使得互连的物理尺寸小于信号波长的十分之一时，我们可以假设沿线的不同点处于相同的电势并具有相同的电流。

从实用的角度来看，这是一个令人满意的假设，大大简化了低频电路设计。然而，当我们进入更高的频率时，我们可能需要将信号描述为沿着电线传播的波。在这种情况下，信号幅度是时间和位置的函数。

电压波沿导线传播的信号

例如，考虑通过一对长线将源阻抗为Rs的正弦输入Vscos（⍵t）应用于负载阻抗RL（图1（a））。

使用一对长线的示例（a）、时间正弦函数的波形（b）和示出沿线电压的波形（c）。

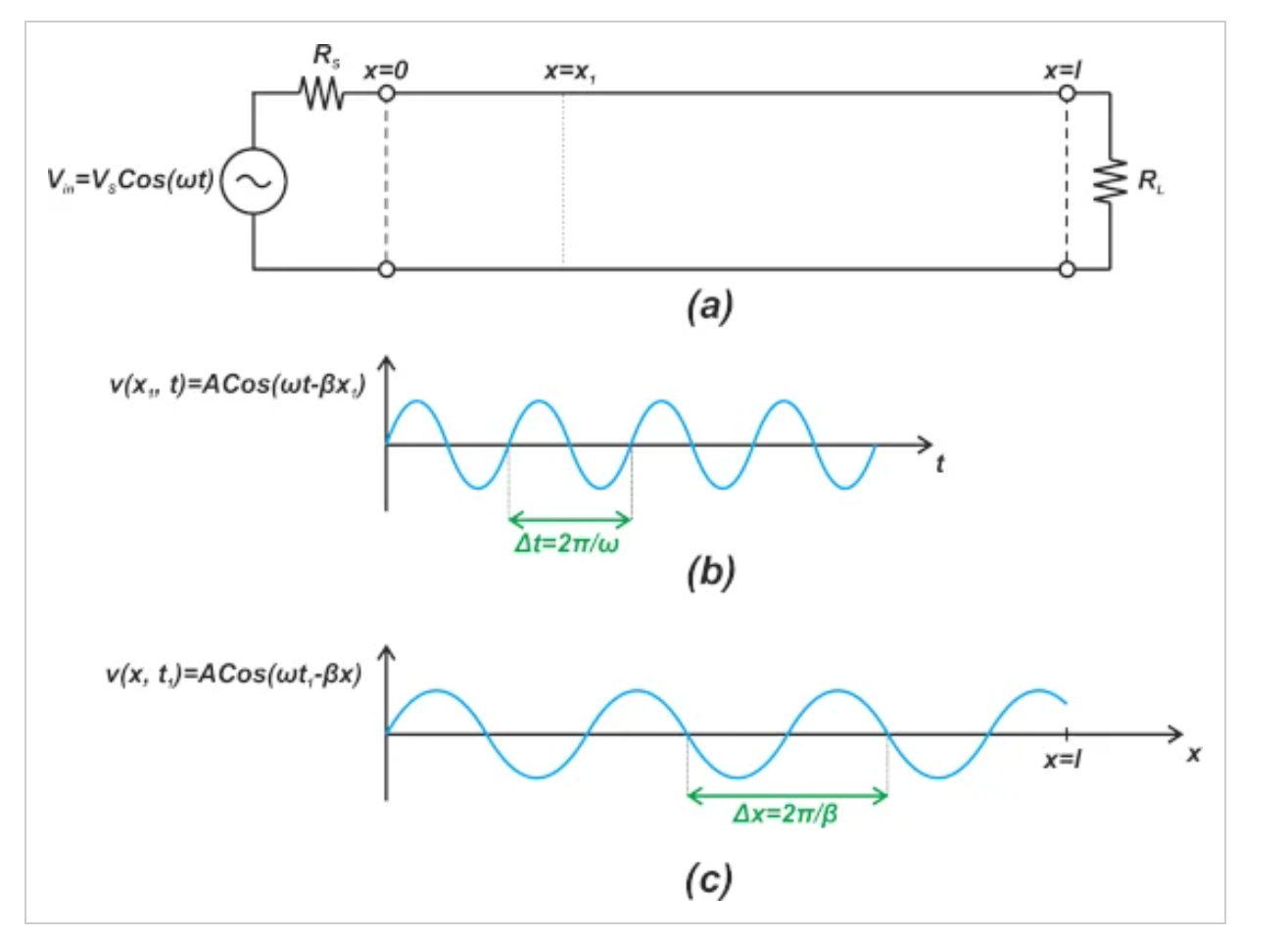
图1 使用一对长线的示例（a）、时间正弦函数的波形（b）和示出沿线电压的波形（c）

假设x轴方向上的导线长度远大于信号波长。此外，假设互连具有均匀的结构，不同的参数，如导体尺寸、导体之间的间距等，沿导线是相同的。

沿导线出现的稳态电压和电流信号取决于许多参数的值；然而，为了对该电路的行为进行定性描述，我们假设电压波可以用方程1来描述：

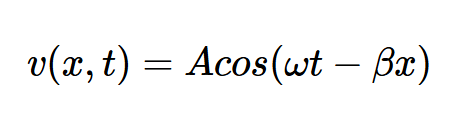
方程式1

其中A和β是取决于电路参数的一些常数。如图所示，电压信号是时间（t）和位置（x）的函数。在固定位置x=x1，βx项是一个恒定的相位项，上述波形只是时间的正弦函数（图1（b））。该正弦函数的周期T为：

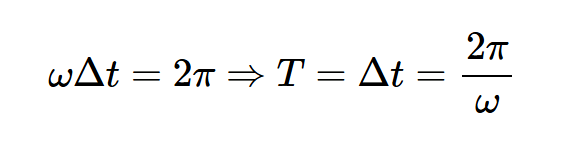
为了检查与位置有关的波形依赖性，我们可以查看时间t=t1中特定时刻的波形。在这种情况下，项⍵t变成了一个恒定的相位项，我们观察到电压信号是位置x的正弦函数。图1（c）中的示例波形显示了在给定时间点，沿着导线的电压如何沿着互连正弦变化。该波形可视为x在导线长度上的周期函数。该期限由以下公式给出：

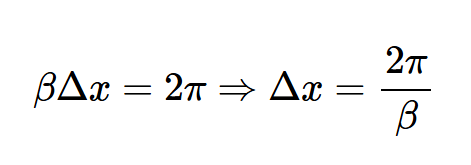
上述方程指定了在给定时刻沿导线的信号的两个连续相等值之间的距离。这实际上是通常由方程2表示的波长的定义：

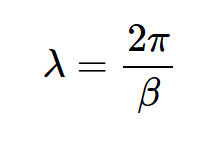
方程式2

传播方向和速度

就像水波在特定方向上传播一样，电波也在特定方向传播。作为一个例子，考虑方程1中的波函数。在给定时间（t2），位置（x2）处的函数值为：

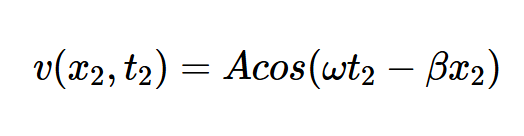
考虑到这一点，假设该值对应于图2（A）中的点A。

示例波形，其中（a）示出位置（x2）为a，（b）示出向右移动的位置（x3）为a。

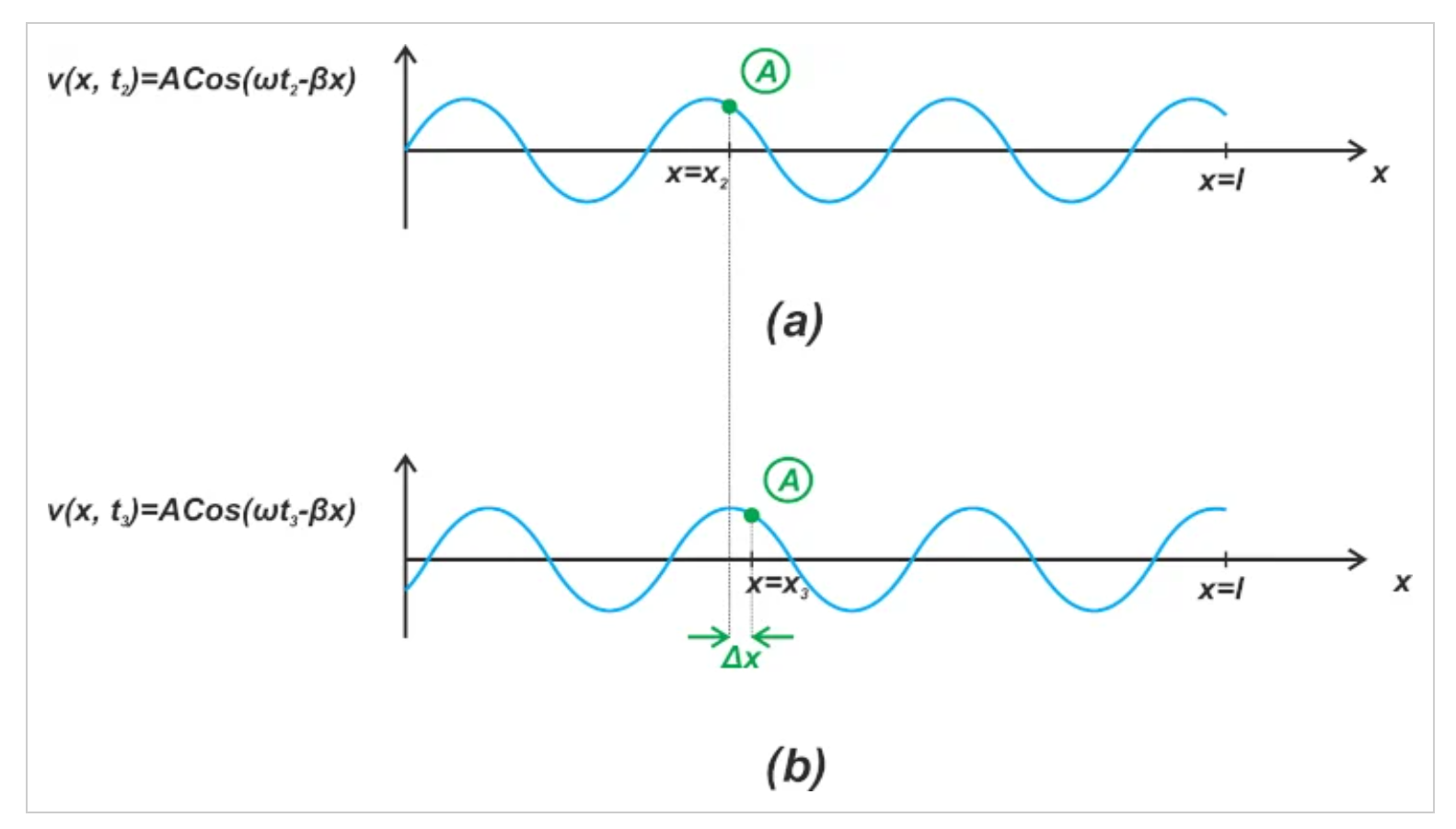
图2 示例波形，其中（a）示出位置（x2）为a，（b）示出向右移动的位置（x3）为a

随着时间的推移，点A将朝哪个方向移动？如果点A的下一个位置是时间t3的x3（图2（b）），我们应该有：

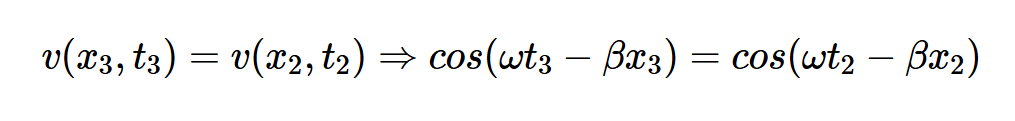
这简化为方程式3：

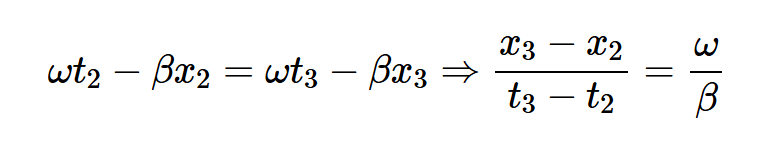
方程式3

假设β为正值，并注意t3>t2，x3应大于x2。换句话说，点A在正x方向上移动。然而，你可能会想，方程4中的以下波函数呢？

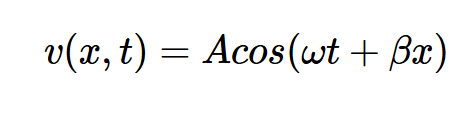
方程式4

该波上给定点的下一个位置对应于保持⍵t+βx恒定的x值。由于项⍵t随时间增加，x应该减少。因此，该波沿负x方向传播。方程3实际上给出了传播速度（也称为波的相速度（vp））：

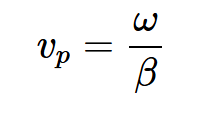
射频波反射

幸运的是，各种类型的波，包括机械波、电波、声波和光波，其行为基本相似。这有助于我们利用我们对更具体类型（如水波）的直觉，更好地理解其他类型的行为。各种波的一个相似之处是，当它们所穿过的介质的某些特性发生变化时，它们会反射出来。

例如，当向岸边行进的水波与岩石碰撞时，它会被岩石反射并传播回海洋。类似地，当波介质的阻抗变化时，电压波会反射。

在图1（a）所示的示例中，当负载阻抗RL与称为特性阻抗（通常用Z0表示）的互连的特殊属性不匹配时，沿正x方向传播的波会反射。反射后，产生从负载向电压源传播的负x方向的波。因此，一般来说，我们可以预期入射波和反射波会同时沿着导线传播。反射电压与入射电压的比率被定义为反射系数，并表示为

阻抗匹配：射频工程师的困扰

由于一些入射功率被反射回源，负载无法接收源提供的最大功率。因此，反射系数是一个重要参数，它决定了实际有多少可用功率会到达负载。为了实现最大的功率传输，负载阻抗应与线路的特性阻抗相匹配。

负载失配的另一个问题是，入射波和反射波的叠加会沿导线产生较大的峰值电压，从而损坏我们的电路组件或互连。上述讨论表明，在处理高频信号时，我们需要具有精确控制参数的互连来预测波沿互连传播时的行为。例如，应精确控制导体的尺寸、导体之间的距离以及分隔导体的电介质类型。这些专门的互连被称为传输线，以区别于普通互连。

射频波尺寸

根据经验，如果导线的物理长度约为

  $$\frac{\lambda }{15}$$

，电信号应被视为通过电线传播的波。

图3帮助您可视化如何将导线长度限制为

  $$\frac{\lambda }{15}$$

减少了信号随位置的变化。

通过限制导线尺寸（a），显示信号如何随位置（b）变化的示例

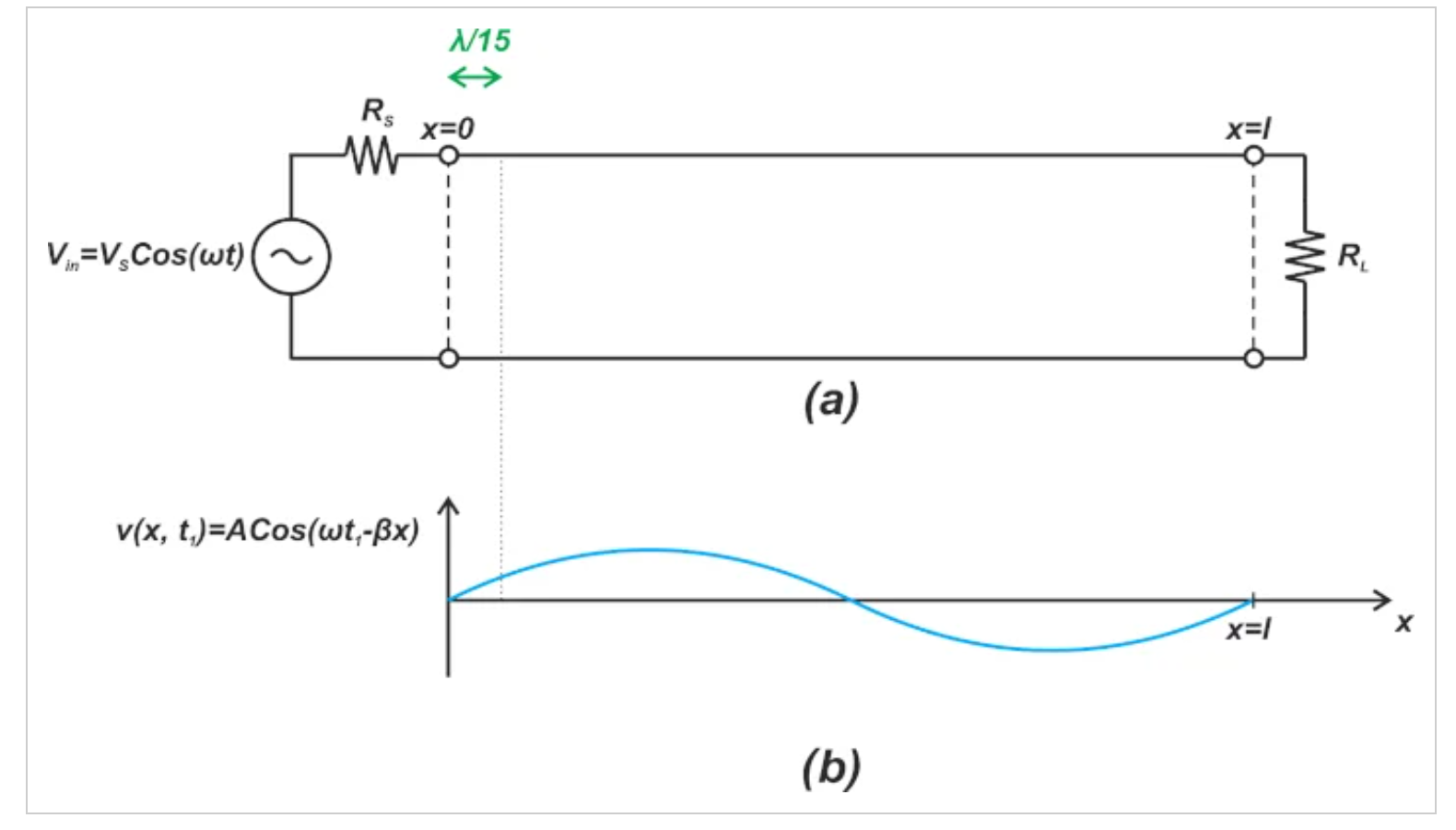
图3 通过限制导线尺寸（a），显示信号如何随位置（b）变化的示例

一些参考文献建议物理尺寸为

 $$\frac{\lambda }{10}$$

作为预期信号随位置变化显著的阈值。

现在我们对电波和传输线有了定性的了解，让我们看看传输线的等效电路，看看如何消除反射。

输电线路等效电路

当导线尺寸与波长相当时，我们处理的是沿导线传播的电波。在这种情况下，基尔霍夫电路定律（电压定律和电流定律）不能直接应用。然而，我们仍然可以找到高频下双导体互连的等效电路。为此，线路被划分为长度无穷小的元素，每个元素都被建模为由电感器、电容器和两个电阻器组成的网络。如图4所示。

一个显示传输线元件的示例：电感器、电容器和两个电阻器。

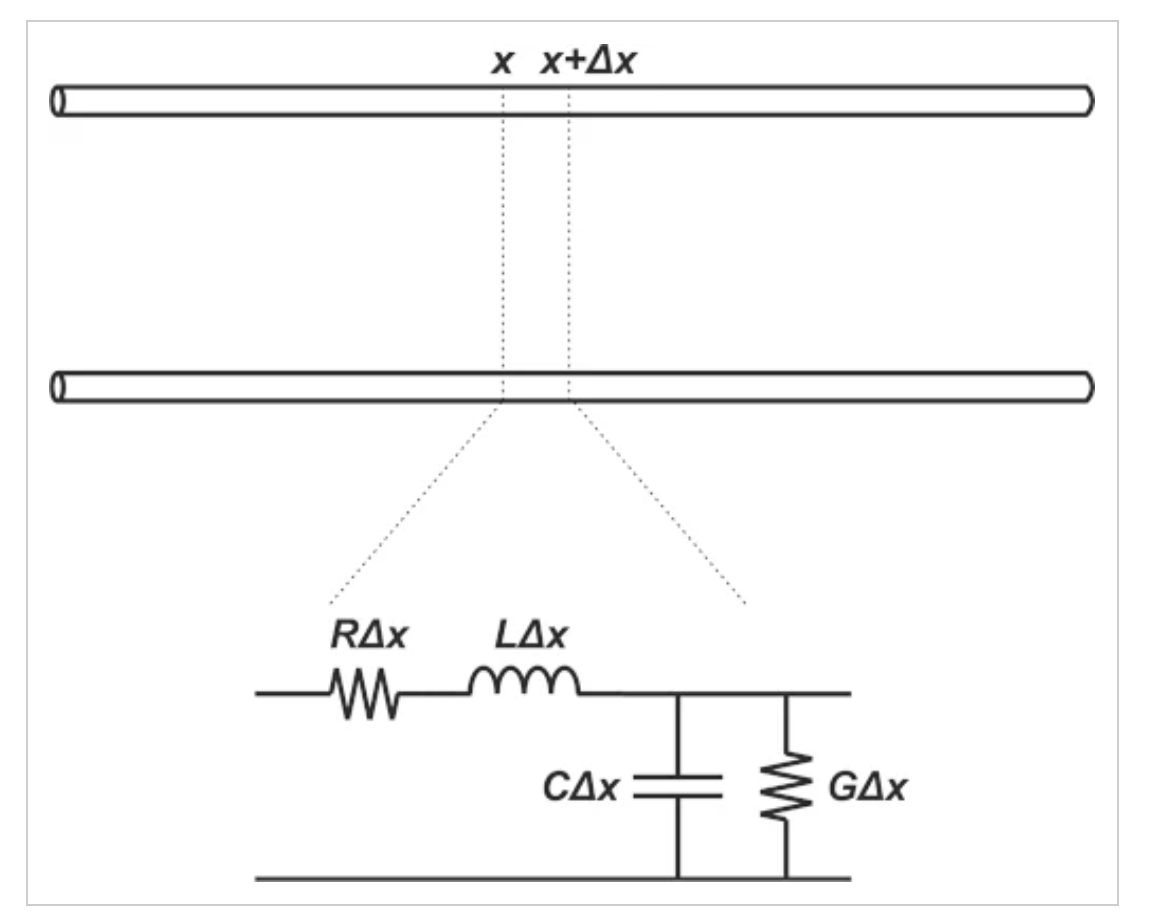
图4 一个显示传输线元件的示例：电感器、电容器和两个电阻器

这里，R和G分别表示导线的单位长度电阻和分隔导体的电介质的单位长度电导。L和C表示传输线每单位长度的电感和电容。

在射频下，串联电抗通常远大于串联电阻，分流电抗通常远小于分流电阻，因此我们可以假设这两个电阻都可以忽略不计。忽略R和G分量，无损传输线可以用图5所示的无限梯形网络来建模。

无限梯形网络的模型。

图5 无限梯形网络的模型

通过阻抗匹配消除反射

对于无限长的传输线，入射波将永远向前传播，不会有反射！让我们看看我们是否可以通过适当地选择实际有限长度传输线的参数来模拟这种理论情况。对于无限长的传输线，等效电路中有无限数量的段，如图5所示。

如果我们在这个无限梯形网络中添加另一个无穷小的部分，输入阻抗应该保持不变。换句话说，如果图6中的图对应于无限长的传输线，则从节点A和B“看到”的输入阻抗是相同的。

无限长传输线的一个例子。

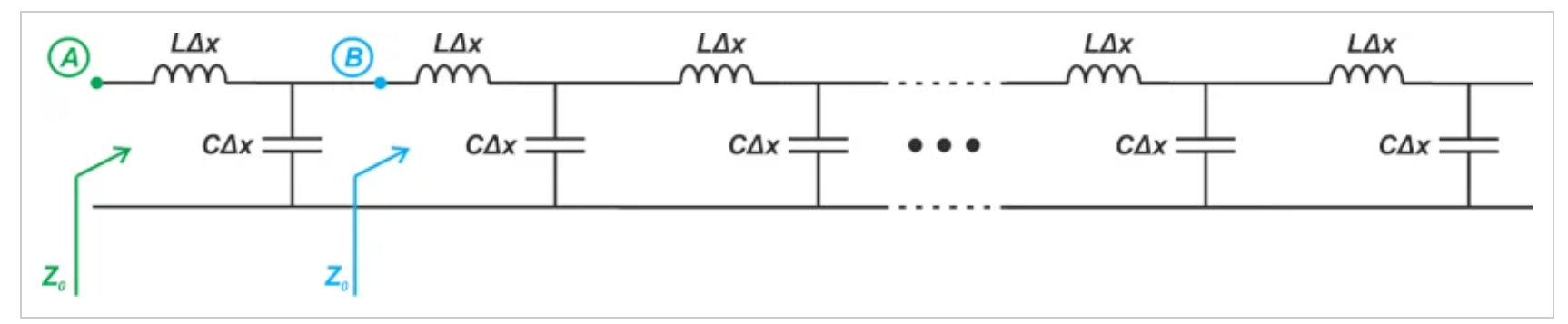
图6 无限长传输线的一个例子

因此，我们可以简化上图，如图7所示。

图6中无限长传输线示例的简化。

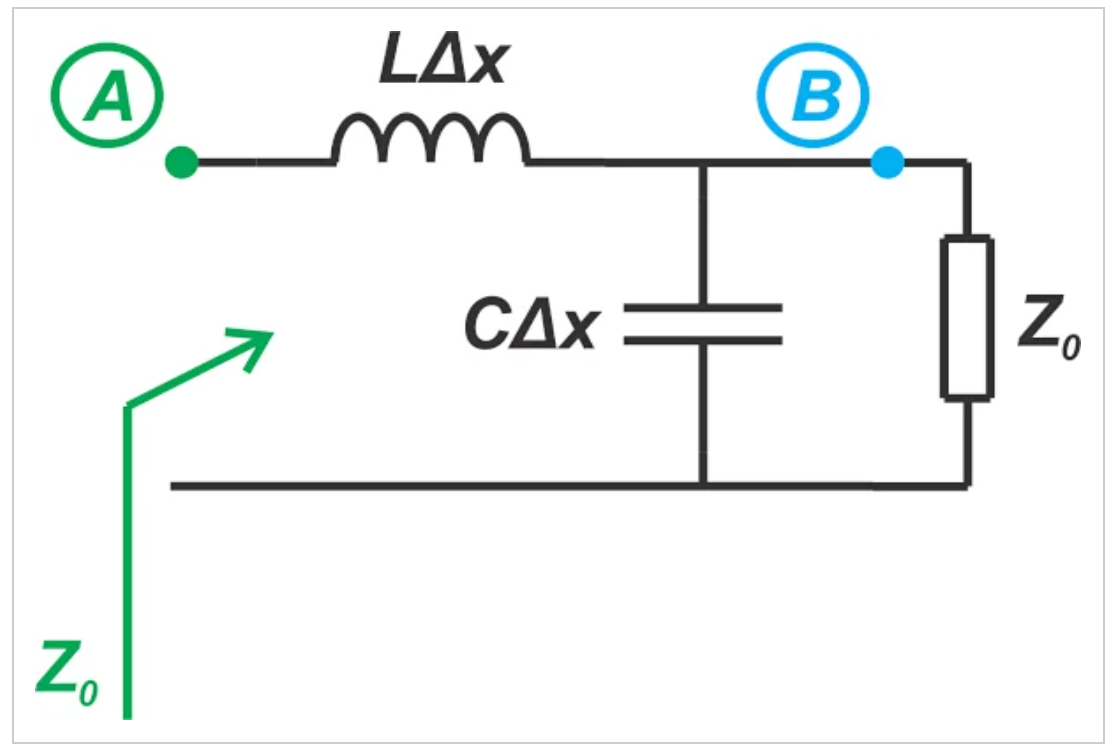
图7 图6中无限长传输线示例的简化

从该图可以看出，输入阻抗为：

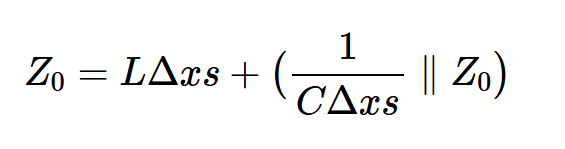
使用一点代数，我们得到：

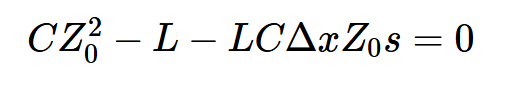
由于Δx $$\to$$ = 0我们可以忽略第三项，从而得到：

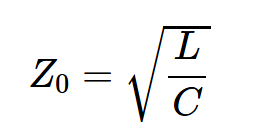
上述方程给出了理想、无损、无限传输线的输入阻抗。由于这是传输线的一个重要特性，因此它被赋予了一个特殊的名称：传输线的特性阻抗。我们如何利用这些信息来消除有限长度传输线中的反射？如上所述，从源的角度来看，图6和图7中的电路是等效的。这表明，如果我们将传输线端接到等于线路特性阻抗的负载电阻器，从源的角度来看，传输线将呈现为无限长的线路，并且不会发生反射。

一个耗散能量的无功组件网络！

有趣的是，虽然整个网络由电抗元件组成，但输入阻抗是一个正的实际值。纯无功元件不能耗散功率；然而，上述分析表明，整个网络可以用一个电阻器来建模，因此，它正在消耗能量！

答案在于，假设网络的长度是无限的。这样的结构是一个有趣的抽象概念，但在物理上是不可能的。在无限长的输电线路中，能量永远沿着线路传播。它不会被任何电感器或电容器消耗。这条线就像一个能量黑洞。

当我们设置RL=Z0时，负载电阻器以无限长的传输线可以永远吸收能量的方式永远耗散能量。因此，反射被省略了。