推论先天八卦与整数树

当前快速发展的信息化引发的信息爆炸，使计算机软、硬件的处理能力已接近极限。原因是我们所使用的计算机是为处理线性数据设计的，对非线性数据一直是通过转换来处理。随着计算机要处理的非线性数据的增加，必然会使计算机数据处理能力不断下降。

今后大范围的云计算、物联网，乃至智慧地球的应用中的无限天量非线性数据处理的需求，促使计算机软、硬件在提高非线性数据的处理能力上创新。

计算机进行数据处理的基本操作是将数据按一定算法程序，在计算机系统内的不同存储单元间移动。数据移动的速度决定计算机数据处理的能力。因此，数据存储技术是提高计算机软、硬件的数据处理能力的核心技术。又因，数据存储技术的基础是数据结构，发明或发现新的数据结构，将是提高数据存储技术的探索方向。

北斗时空码采用北京乾坤化物数字技术有限公司的自主知识产权的“IP地址结构树的构建方法”发明专利建立的索引系统能够快速提供无限天量编码，就是在发现源于先天八卦的整数树数据结构基础上，做了进一步创新后实现的。

一、以往看先天八卦与数

先天八卦是中国宝贵的历史文化遗产。相传先天八卦是由中华民族的先祖伏羲画的。由于没有文字记录，对先天八卦的来历无从考证。但是，几千年来，对先天八卦的含意，人们从各种学科角度进行了一代一代的不懈研究，得出了后天八卦、易经等许多富有哲理的深奥结果，有些推论至今还有很大影响。

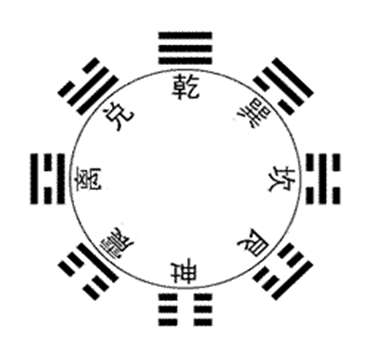
 图1： 先天八卦图

先天八卦是图1圆圈外用阳爻“—”和阴爻“- -”两种连和断的横线，以三层不同组合的八种卦的图形排列的圆形图案。圆圈内的文字是后人研究先天八卦赋给的每个卦的卦名。圆圈是为能明确分隔卦与卦名加画的，没有含意。

从数学角度看，古人对先天八卦产生的最有意义的推论是：太极生两仪：阳仪、阴仪；两仪生四象：太阳、少阴、少阳、太阴；四象生八卦：乾、兌、离、震、巽、坎、艮、坤；八卦生无穷。此推论是一种从哲学角度解说世界是从无到太极，从太极开始生两仪，并按一分为二方式不断分裂产生的。

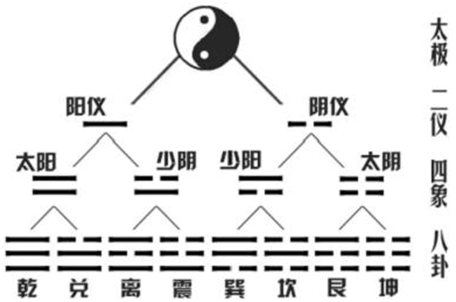
图2：太极产生先天八卦图

古人对太极产生的八卦又分别注上八个数字，即为：乾一、兌二、离三、震四、巽五、坎六、艮七、坤八。由此，指出八卦图中相对应的两卦：乾坤、兑艮、离坎、震巽卦的和都是九。

德国数学家莱布尼兹发明二进制后，有人将先天八卦中的阳爻“—”定义为1，将阴爻“- -”定义为0；然后将先天八卦的八个卦分别注上二进制，即：乾为0：000、兌为1：001、离为2：010、震:为3：011、巽4:100、坎5：101、艮6:110、坤为7：111。也指出用二进制定义八卦后，八卦图中相对应两卦：乾坤、兑艮、离坎、震巽卦的和都是7：111。

近代，数学家用a表示先天八卦中的阳爻“—”，用b代表阴爻“- -”，然后代入(a＋b)的n次自乘的牛顿二项式公式，准确推论出太极生八卦、八卦生无穷的每次生卦的数量和卦的组合状态。经论证，可以看到先天八卦的生卦与二项式公式完全吻合，不尽让人另眼看先天八卦深奥的数学含义。

二、另眼看先天八卦与数

用数字一至八表示先天八卦中的每个卦，还是用二进制000至111表示先天八卦中的每个卦都是人为的定义，不一定代表原画卦者的初衷。数字0的出现和广泛使用是在12世纪，因此，将先天八卦中的阴爻“- -”看做为0进行推论，不符合历史实际。

由于用数字一至八或用二进制数000至111表示先天八卦中的每个卦，都是在人为的，或静态的看先天八卦，不能将每个卦之间的客观关系和每次生卦的动态生长关系表示出来。因此，在数学上一直没能对先天八卦进行更深的推论。再加上一些古人推论八卦与观测星象、预告未来等有关，但因其中许多推论与现代科学不符，越来越不被世人信服，反使先天八卦日益受到冷落。

世间的创新，首先是思路和方法的创新。以往对先天八卦的数学探讨，都是先在主观上定个假设，再进行推论，没看到先天八卦的实质。即然画出先天八卦的时代还没有文字，不仿将爻的图示简单地进行直观：将先天八卦中的阳爻“—”还看做1，将阴爻“- -”就看做2，再观太极生八卦图就会产生新的思路。

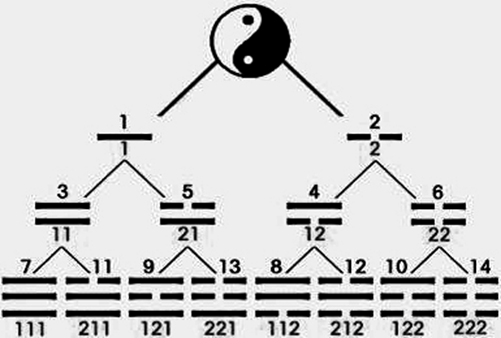图3：另眼看太极生八卦图

图3与图2是一样的太极生八卦图，只是将图2中的二仪、四象和八卦的文字标识去掉，改注了数字。图3中的二仪、四象和八卦的上部标的是十进制数，下部标识的是将二仪、四象和八卦的阳爻“—”替代为1，阴爻“- -”替代为2的对应一组数字表示符。从图3中，可以看到用1和2标识阳爻和阴爻是非常直观和清晰，也许更客观地贴近画先天八卦者的思想。图4是用1和2对应标识阳爻和阴爻的先天八卦图。

三、二的幂次方进制数

为进一步推论先天八卦中的数字关系，将图3中每个二仪、四象和八卦的下部替代阳爻“—”为1，阴爻“- -”为2的对应一组数字表示符，以及图4中对应各卦的由1和2组合的一组数字表示符，定义为是二的幂次方进制数。

表1是十进制1至16与对应二进制、二的幂次方进制数对照表。 

表1：十进制1至16与对应二进制、二的幂次方进制数对照

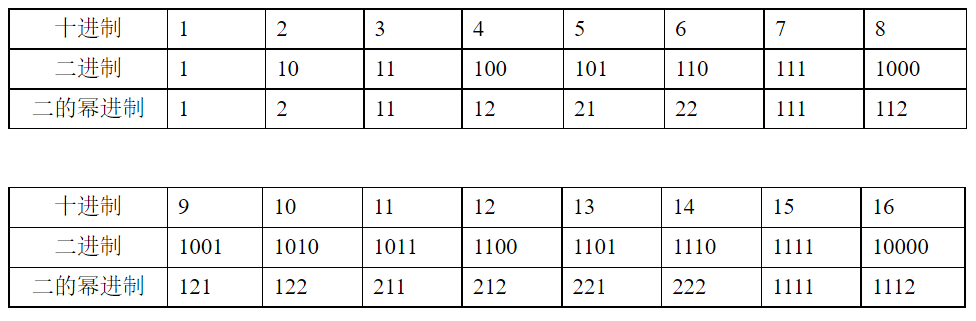
二的幂次方进制数是一种新的计数方法，它由两个基本数字符号1，2组成（也可以规定为0和1或A或B等）。二的幂次方进制数还有一个字符：0 （也可以规定为3或C等），用于表示第三种状态，如：相等、起始、高阻态等。在二的幂次方进制数中，0不用于表示数，但做为正、负整数树的起点（根）存在。如同太极，无形无质，无声无臭；可是它有神有气，有灵有显，可以无中生有。

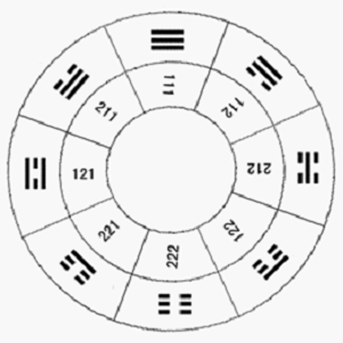
 图4 ：用1和2对应标的先天八卦图

二的幂次方进制数计数规律是满二的幂次方值时向上位进一，且进位位恢复系数为1。为符合人们日常十进制运算习惯，我们将二的幂次方进制数中，用数字符号1直接表示整数1，用数字符号2直接表示整数2，可使这二个数字符号的表示与十进制的整数1和2相同。整数3以后的整数也用1或2两数字符号表示。如：整数3将产生进位，用两位数字符号11表示，整数4不产生进位，用两位数字12表示，整数5产生进位，用2位数字21表示，整数6不产生进位，用两位数字22表示，整数7产生两次进位，用三位数字111表示……。由此可以看到：二的幂次方进制数对应N位整数Z的表示应为：

           Z= X(N)X(N-1) …X(N-N+3)X(N-N+2)X(N-N+1)X(N-N)

其中，X={1,2}，X数字符号，N={0,1,2…}, N是位数。

每个整数在二的幂次方进制数中仅表示出每位的数字符号，省略了每位对应的数位的权，即二的幂。这与十进制、二进制和十六进制等数字表示时省略数位的权一样。^注1

图3中的二仪、四象和八卦的上部标的十进制数就是每个二仪、四象和八卦的二的幂次方进制数对应的十进制数。图5是用十进制数标识的先天八卦图。

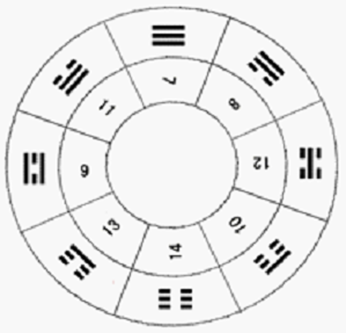 图5：用十进制标识的先天八卦图

从图5中也可以看到用十进制表示先天八卦中各卦后，八卦图中相对应两卦：乾坤、兑艮、离坎、震巽卦的和都是十进制数21。还可以看到从乾卦逆时针的乾、兑、离、震四卦对应的十进制数7、11、9、13都是奇整数，从巽卦开始顺时针的巽、坎、艮坤四卦对应的十进制数8、12、10、14都是偶整数。这是从先天八卦转换出来的非常有创新意义的数据结构。

四、二的幂次方进制数标识八卦生无穷

二的幂次方进制数是将古人用阳爻“—”和阴爻“- -”两个符号表述：无极生太极、太极生二仪、二仪生四象、四象生八卦、八卦生无穷的生变过程，用现代人习惯的用1代替阳爻“—”，用2代替阴爻“- -”后再次标识产生，与古人用爻表示是一一对应的。因此，二的幂次方进制数不是新发明，仅用新符号表示先前已存在的数据结构。

从图2、图3中可以看到太极生八卦图是以太极为根的二叉树。由太极生出两个子结点：奇数结点和偶数结点 分别为二仪。用阳爻“—”表示奇数结点阳仪，用阴爻“- -”表示偶数结点阴仪。再生变，两仪又做父结点，各生出两节点分别为四象。再生变，四象又做父结点，各生出两节点分别为八卦。然后再生变，八八生六十四卦，乃至可生出无穷。将此种结构的二叉树，定义为整数二叉树。图6为古人的六十四卦图。

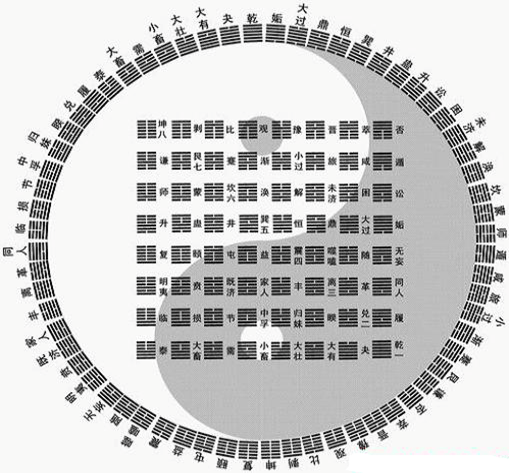
图6：六十四卦图

用1代替a，用2代替b，并且n=1、2、3……，展开二项式公式(a+b)ⁿ可得到如下结果：

(a+b)¹=(1+2)¹=1+2

(a+b)²=(1+2)²=(1+2) (1+2)=11+21+12+22

(a+b)³=(1+2)³=(1+2)²(1+2)=( 11+21+12+22) (1+2)

=111+211+121+221+112+212+122+222

…………

   将上述每次二项式公式展开得到的数，看做是二的幂次方进制数，将第1式展开数1、2摆在上层，再将后两式展开数，依此按层向下排列如下：

用阳爻“—”和阴爻“- -”分别代替展开结果中各项的1和2。然后将替代后的每个爻的组合，按最左侧爻在上，最右侧爻在下的顺序排，就可看到与图3：古代太极生两仪、两仪生四象、四象生八卦相同图。由此，可以证明二的幂次方进制数与先天八卦的对应关系。图7是用二的幂次方进制数和对应十进制数表示的六十四卦图。

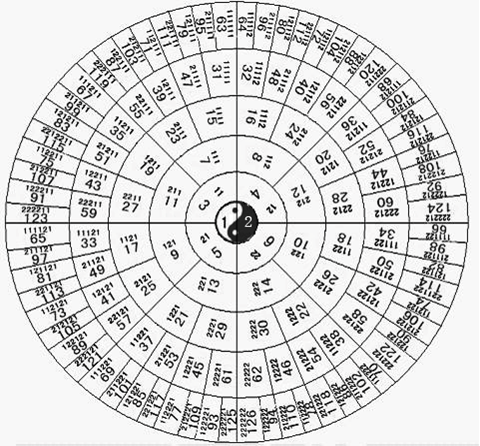
  图7：用二的幂次方进制数和对应十进制数表示的六十四卦

将图7最外层每个二的幂次方进制数与图6中六十四卦所对应的每个卦相比较，可以看到都是一一对应相同的。只是用1或2表示，还是用阳爻“—”和阴爻“- -”表示的不同。

从图7中的中心园的1和2到最外层圆的各二的幂次方进制数是按一生二的规则生变的，而且非常简单。每个奇数子结点的二的幂次进制数是其父结点二的幂次方进制数前放置1产生，每个偶数数子结点的二的幂次进制数是其父结点二的幂次方进制数前放置2产生。这与用爻表示太极生二仪、二仪生四象、四象生八卦、八卦生无穷的生变过程：即每生变一次结果是在生变前的用爻表示的图形上添画一个阳爻“—”产生左边（奇数）子图形，添画一个阴爻“- -”产生右边（偶数）子图形是完全一样的。用二的幂次方进制数标识太极生八卦、八卦生无穷会更直观。

引入二的幂次方进制数的更重要意义是，可以用数学计算与先天八卦生变过程对应的数据结构：整数二叉树。

五、先天八卦揭示的整数二叉树

将图3太极生八卦图中的太极用0代替，并将二仪、四象和八卦图形去掉，再多生变一次（多显示一层整数二叉树），可得到图8所示的整数二叉树最顶的四层结点的数据结构。

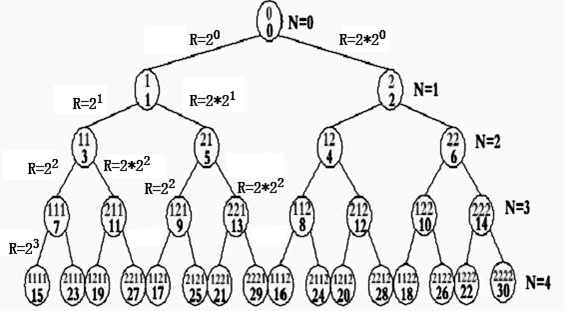
图8：用二的幂次方进制数和十进制表示的四层整数二叉树

图8中圆圈为整数二叉树的每个结点，圆圈内上部数字为用二的幂次方进制数表示出的整数的结点代码，下部数字为与结点代码对应的十进制整数。字母N表示整数树的层数，字母R表示各父结点与子结点的差值。

整数二叉树最顶的父结点是整数二叉数的根，其结点代码和对应十进制数都为0。由根的父结点生长（生变）出二个子结点1和2结点，由此不断生长，长成无限层的整数二叉树。

整数二叉树上每个子结点值的生长公式为M_N+1 = M_N + X*2^N，这是一个递归方程式，其中X={1,2}，X是数字符号，代表整数二叉树的2个子结点数。N={0,1,2,…}, N是整数分布的层数，M_N 为第N层一个父结点的整数值，M_N+1 是要计算出的M_N的子结点整数值。当N=0时，M_N =0，它表示整数二叉树的开始，对于N>0的任何一个M_N ，其子整数有并且必须有2个，分别为M_N+1 = M_N + 1*2^N，M_N+1 = M_N + 2*2^N。

从图8中可以看到整数二叉树有以1为父结点的全部各层结点都为奇数的子结点分叉树和以2为父结点的全部各层结点都为偶数的子结点分叉树。这是整数二叉树数据结构的重要特点。理论上整数二叉树还应有负奇数和负偶数两个分叉树，在此不做推论。

从整数二叉树的图8中可以明显看到一些规律：

1、整数按奇数和偶数有规则地组成为两个分叉树。

2、每层的结点数为2^N个，N为层数。

3、每个父结点有两个子结点：奇数子结点和偶数子结点。父结点与奇数子结点间的差值R= 2 ^N，与偶数子结点的差值R=2* 2 ^N，N为父结点的层数。

4、两个子结点之间差值为父结点与奇数结点的差值R=2 ^N，N为父结点的层数。

5、每层各结点的二的幂进制数结点代码的位数都等于该层的层数N。

6、每层各结点的二的幂进制数结点代码值都等于该结点十进制整数值。

7、每层各结点的二的幂进制数结点代码和对应十进制整数值的位置固定不变等等。

对整数二叉树进行深入的研究，会对整数产生更多的认识和新的算法。支撑北斗时空码的无限天量编码可通过快速计算产生存储地址的索引系统的核心技术，主要源自上述整数二叉树的规律。

例如，要对整数28进行存取的操作，先将28通过计算转换成二的幂次方进制数（注1）2212，实际2212已是28的存取地址码。然后可采用多种方法可找出存取28的结点。方法一是通过2212可知28存取得结点在整数二叉树的第4层，直接到该层用某种算法去找。方法二是从28算出的二的幂次方进制数2212的最右侧（最低位）数开始，逐位判别是1还是2，决定从根结点0开始判别位是1向左下行至下一层结点，是2向右下行至下一层结点，以此类推，一个整数计算得出几位二的幂次方进制数就判转几次，最后到达的结点必是要找的结点。

继续以2212为例，从根结点开始，因2212最右数为2，要先右下行一层，2212的右数第二数为1，再左下行一层，然后2212右数第3和第4数都为2，再连续右下行两层，就到整数28要存取的结点（图8中第四层的从左数第12个结点），此结点永远是存取28这一整数的结点。

客观存在的事实是：无论多大和多小的整数，在整数二叉树上都固定有自己对应的结点。此结点的地址码就是该整数的二的幂次方进制数。

六、整数无穷叉树与无穷幂次方进制数

数学源于自然数的计数。数学的发展，在自然数的基础上陆续派生出整数、实数、虚数等等。整数是目前用的最多的数。整数是公差为1的整数等差数列，也可看做整数一叉树。如图9所示：

图9：整数一叉树    

 整数一叉树的层数N=0、1、2、3、4……，每层结点数为1^N，都是1个。各结点的差值R=1^N，也都为1。子结点的生长公式为M_N+1 = M_N + X*1^N。式中M_N为M_N+1的父结点，N=0时M_N为0，X为子结点数，此处为1。对于N>0的任何一个M_N ，其子结点有并且必须有1个。

 图10是用十进制数表示的整数二叉树。图中N=3层用深色底标出的八个结点中的数，就是先天八卦排列的八个卦对应的十进制数。从图中可以清楚地看到先天八卦在整数二叉树上的位置。

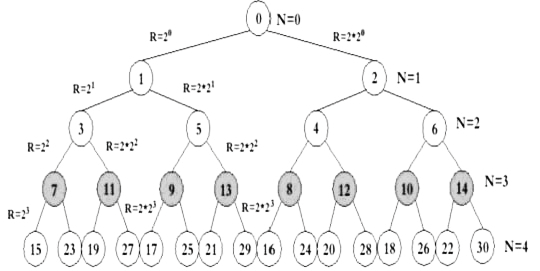
图10：用十进制数表示的整数二叉树

整数二叉树用于数据存取地址索引的方法，在数据量少时，显不出优势。但是在数据量很大时索引速度还不会很快。这是因为，N层整数二叉树上的结点个数Z的计算公式为：Z=2*2^N -1。如果事先知道要处理的最大整数值时，用此公式可算出至少需要多少层的整数二叉树。当整数二叉树层过多时，用在整数二叉树的查找方法，查找整数Z的速度会较慢。

可以推论：整数以一叉树、二叉树数据结构排列外，同样可以按多叉数，乃至无穷叉树排列，而且各个叉树的特点和规律相同。图11是整数三叉树的上三层各结点排列图。

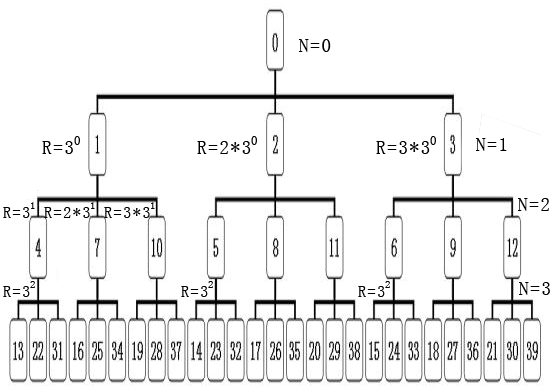
图11：整数三叉树的上三层各结点排列

整数三叉树上每个子结点值的生长公式为M_N+1 = M_N + X*3^N，其中X={1,2，3}，X是数字符号，代表整数三叉树的3个子结点数。N={0,1,2,…}, N是整数分布的层数，M_N 为第N层一个父结点的整数值，M_N+1 是要计算出的M_N的子结点整数值。当N=0时，M_N =0，它表示整数三叉树的开始，对于N>0的任何一个M_N ，其子结点有并且必须有3个，分别为M_N+1 = M_N + 1*3^N，M_N+1 = M_N + 2*3^N，M_N+1 = M_N + 3*3^N。

图12是整数四叉树的上三层各结点排列图。

整数四叉树上每个子结点值的生长公式为M_N+1 = M_N + X*4^N，其中X={1,2，3，4}，X是数字符号，代表整数三叉树的4个子结点数。N={0,1,2,…}, N是整数分布的层数，M_N 为第N层一个父结点的整数值，M_N+1 是要计算出的M_N的子结点整数值。当N=0时，M_N =0，它表示整数四叉树的开始，对于N>0的任何一个M_N ，其子结点有并且必须有4个，分别为M_N+1 = M_N + 1*4^N，M_N+1 = M_N + 2*4^N，M_N+1 = M_N + 3*4^N，M_N+1 = M_N + 4*4^N。

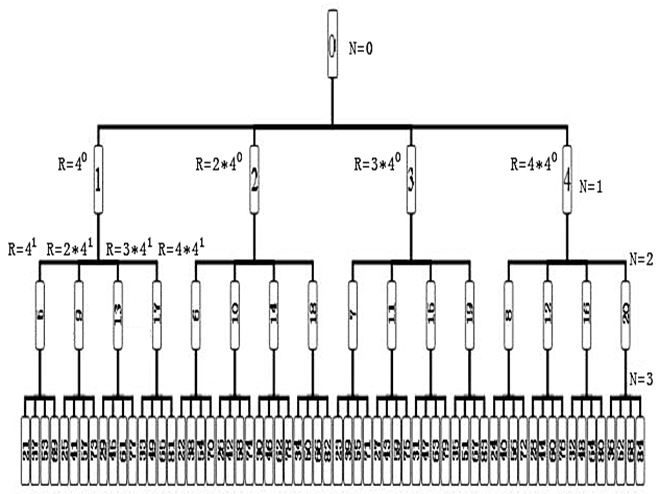
图12：整数四叉树的上三层各结点排列

    以整数三叉树和四叉树产生为例，可以得到整数五叉树、六叉树……Y叉树，直至无穷叉树。

同样以二的幂次方进制数引入方式，可以引入三的幂次方进制数、四的幂次方进制数……Y的幂次方进制数，直至无穷的幂次方进制数。

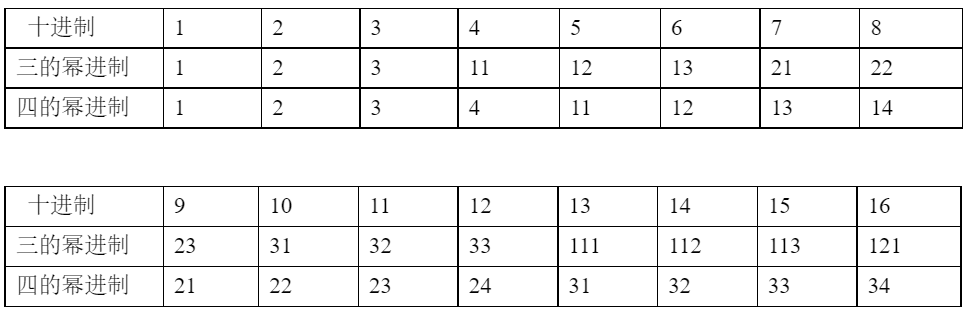
表2是十进制1至16与对应三的幂次方进制数和四的幂次方进制数对照表。      

表2：十进制1至16与对应三和四的幂次方进制数对照

七、结论

一、由先天八卦的生变过程推导出的整数二叉树是整数的一种数据结构。

二、除整数二叉树外还有从一叉树到无穷叉树，统称整数树或整数森林。

三、整数森林中任何一个Y叉树都有无穷多个结点。

四、任何一个整数Y叉树第N层及其上面各层的结点总数Z=2*Y^N -1。

五、任何一个整数Y叉树都有一个与其所有结点位置相对应的Y的幂次方进制数。

六、任何一个整数Y叉树上每个子结点值的生长公式为M_N+1 = M_N + X*Y^N，其中X={1,2，3……Y}，X是数字符号，代表整数Y叉树的Y个子结点数。N={0,1,2,…}, N是整数分布的层数，M_N 为第N层一个父结点的整数值，M_N+1 是要计算出的M_N的子结点整数值。当N=0时，M_N =0，它表示整数Y叉树的开始，对于N>0的任何一个M_N ，其子整数有并且必须有一个，分别为M_N+1 = M_N + 1*Y^N，M_N+1 = M_N + 2*Y^N……M_N+1 = M_N + Y*Y^N。

七、任何一个整数Y叉树上每层的结点数为Y^N个，N为层数。

八、任何一个整数Y叉树上每个父结点有Y个子结点。父结点与第1子结点间的差值R= Y ^N，与第2子结点的差值R=2* Y^N，……与第Y个子结点的差值R=Y* Y ^N， N为父结点的层数。

 九、任何一个整数Y叉树上两个子结点之间差值为父结点与第1子结点的差值R=Y ^N，N为父结点的层数。

十、任何一个整数Y叉树上每层各结点的Y的幂进制数结点代码的位数都等于该层的层数N。

十一、任何一个整数Y叉树上每层各结点的Y的幂进制数结点代码值都等于该结点对应十进制整数值。

十二、任何一个整数Y叉树上每层各结点的Y的幂进制数结点代码和对应十进制整数值的位置固定不变等等。

不断研究和应用整数无穷叉树的特性和规律，选用适合的某一整数多叉树，可以对大数据、无穷天量数据进行快速管理。

几千年来，人类对整数一叉树的研究中，逐步建立了现代数学。一叶先天八卦，揭示整数森林。迈入整数森林，能否寻找到未来数学宝藏，还需更多人去探索。

注1：在网上可查阅“用整数树的研究成果  探索软件的创新发展”一文。