深度学习基础概念笔记

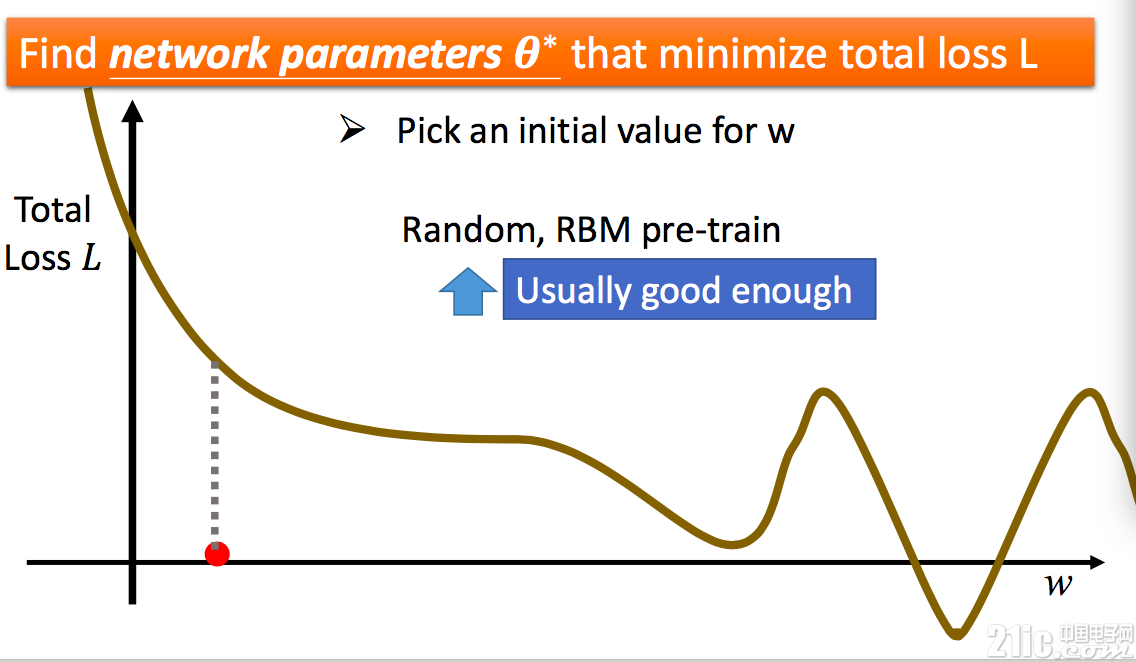
我们都知道，函数某个位置可导，那么就可以确定这个点的斜率。要找到局部最小值，可以根据这个点的斜率移动 w。如根据此时斜率的值我们可以确定 w 应该向右移动一段距离。

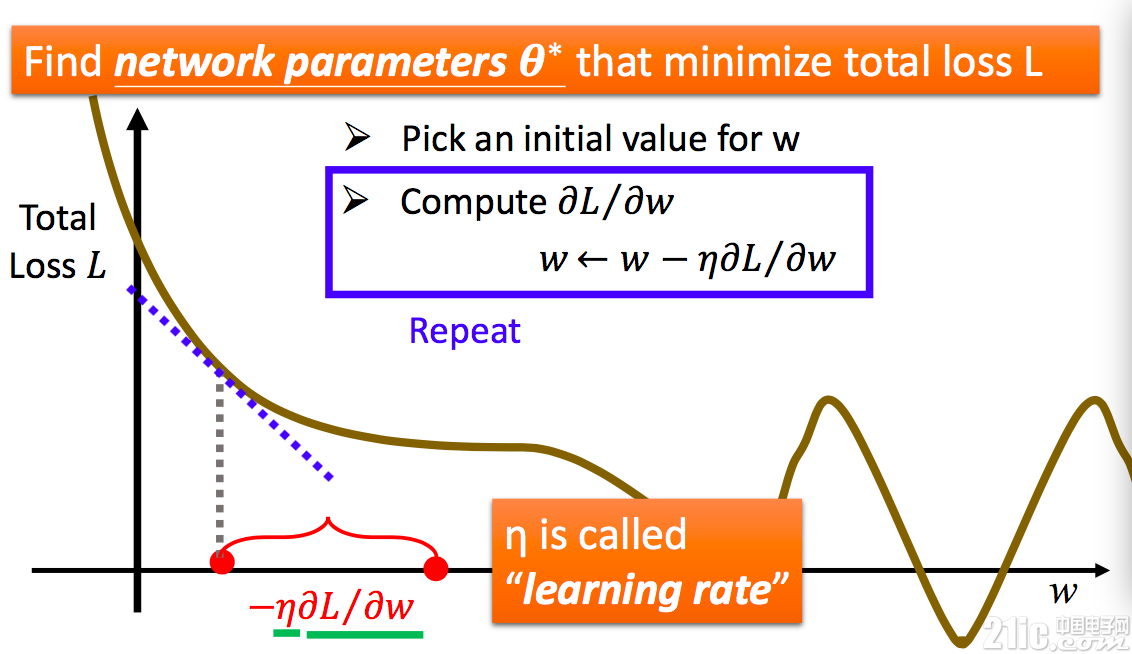
此时移动 w 的距离称为步长。步长的选取很关键，如果步长过长，那么每次 w 偏移过大，永远都找不到真正的最小值。而如果步长选取过小，那么收敛会变得很慢，而且有可能在中间某段平滑处停下来，找到的也不是真正的最小值。而步长怎么选择呢?其实比较坑爹，某些时候有经验值，大部分时候则只能自己调整去试验。

在学习的过程中，遇到的最常见的一个问题是走不动了。比如在下图中。从 A 点走到 B 点，B 点由于斜率平滑，慢慢走到了 C 点，这时候可能 C 点斜率是平滑了，那么 w 将无法继续往下走，永远停留在 C 点!这样得到的神经网络的误差 L 显然不是最小的，权值 w 也不是最佳的。

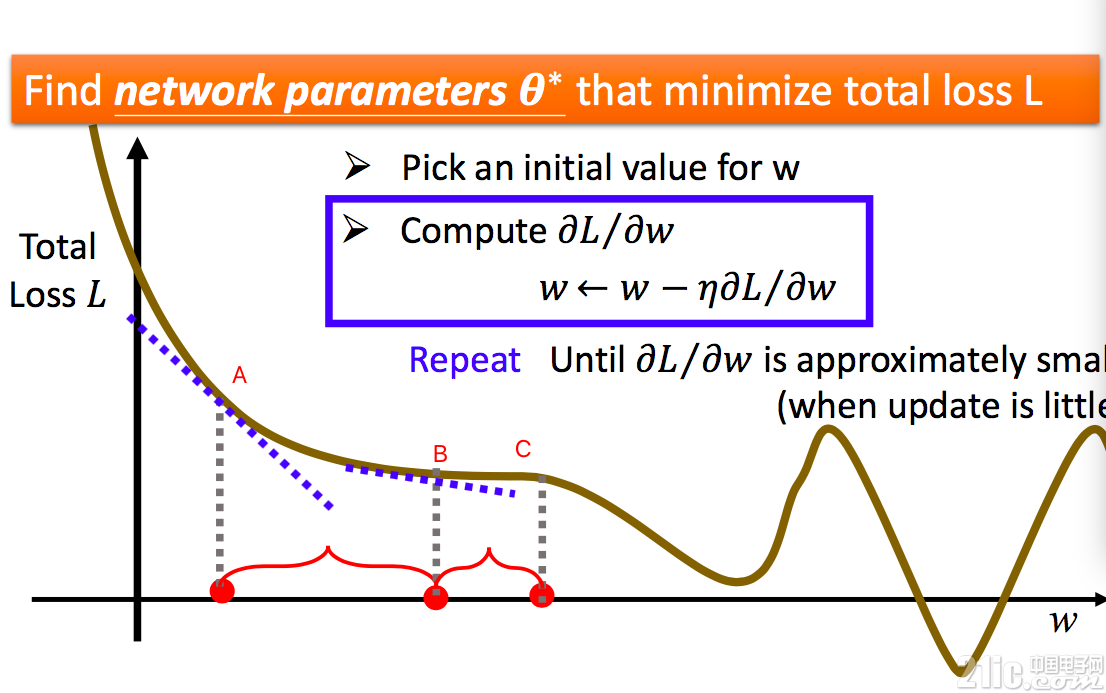
因此，在神经网络学习过程中，常用的做法是模拟物理世界引入一个动量球。假设每次的移动看成 是一个动量球的移动。在移动过程中，动量球先从最高点往下走，虽然下载下来后斜率减少，但是由于动量球将移动下来的重力势能转变的动能，它会继续往下走，从而移动过平缓区。当动量球到达某个局部最低点的时候，动量球会依靠自己的动能继续滚动，设法寻找到下一个局部最低点。当然，动量球不是万能的，它也可能会遇到山坡上不去最终滑下来停留在某个局部最小值(并不是真正的最小值)。但是动量球的引入，大大增加了学习过程的鲁棒性，扩宽了局部最小值的寻找范围。

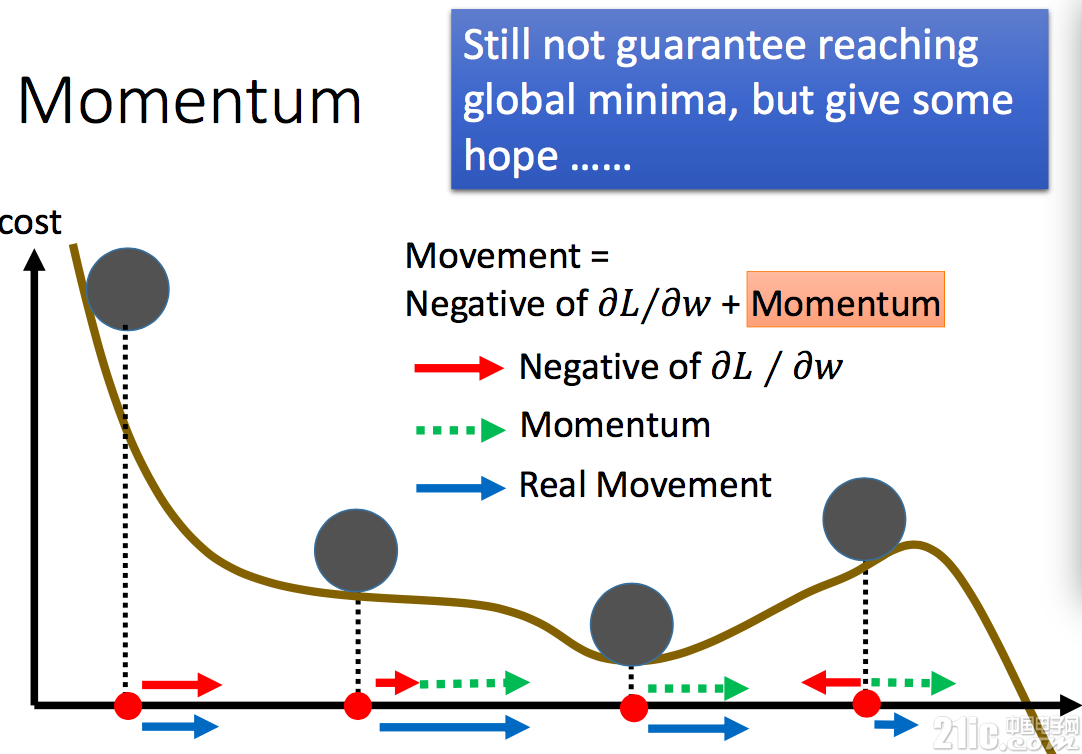
实际上，借助理解神经网络学习的过程，我们会更加理解为什么深度越高的网络不一定就越好。对于深度越高的神经网络，平滑区会越来越多，局部最小点也会越来越多。没有合适的算法，很容易就陷入某个局部最小值里面去，而这个最小值可能还不如深度更浅的神经网络获得的局部最小值小。也就是说，神经网络复杂之后，对架构和算法的要求大大加高。

卷积

如果对卷积这个数学概念还没有了解，可以先看知乎这里通俗的解释。

怎样通俗易懂地解释卷积?

如果没有做过图像处理，还需要先看看卷积核，感受一下它的神奇。

图像卷积与滤波的一些知识点

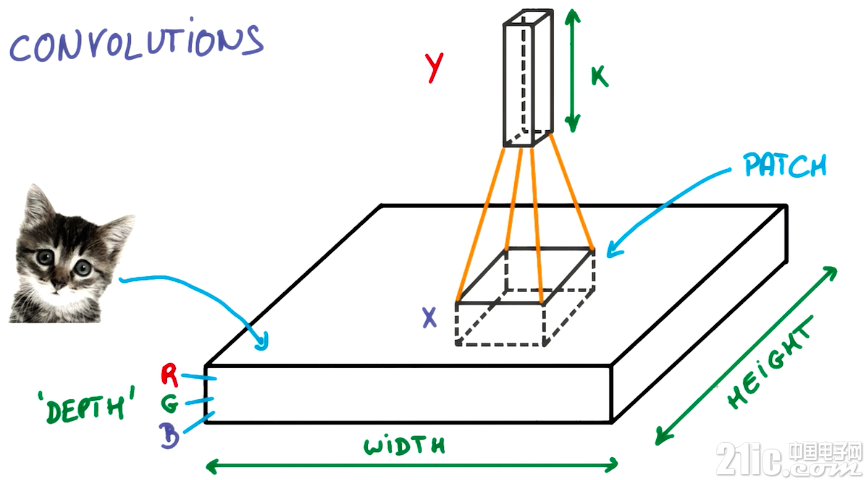
以图片的卷积为例，深度学习中的卷积计算就是使用卷积核遍历一张图片的过程。

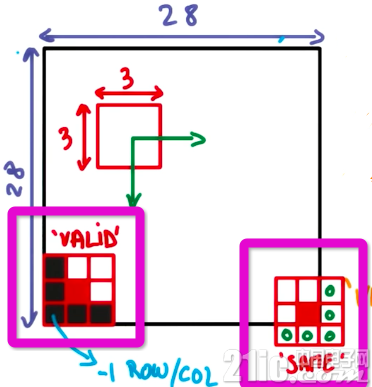
根据对于边缘的处理不同，卷积分为相同填充和有效填充两种方法。相同填充中，超出边界的部分使用补充 0 的方法，使得输入和输出的图像尺寸相同。而在有效填充中，则不使用补充 0 的方法，因此输出的尺寸会比输入尺寸小一些。

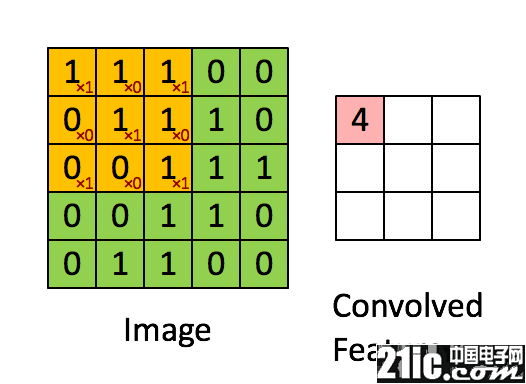
例 1：3*3 的卷积核在 5*5 的图像上进行有效填充的卷积过程

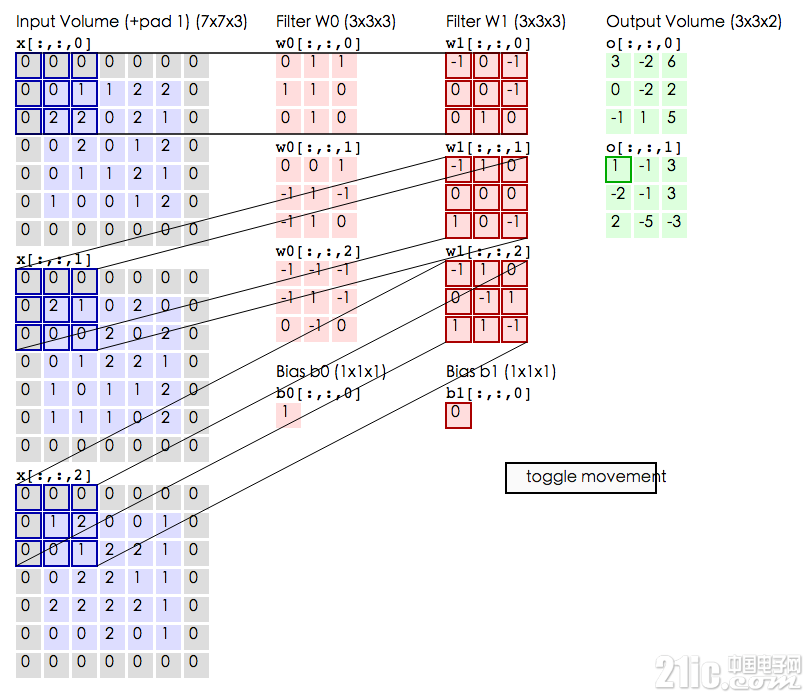
例 2. 两个 3*3*3 卷积核在 5*5 图像上进行相同填充卷积过程。动图

图像有 r，g，b 三个通道。这里使用卷积核也分为 3 个通道分别进行卷积运算

池化

池化是卷积神经网络中用到的一种运算。在卷积神经网络中，卷积层后面一般是池化层。先进行卷积运算，再进行池化运算。

池化层在神经网络中起到的是降低参数和计算量，引入不变形的作用。

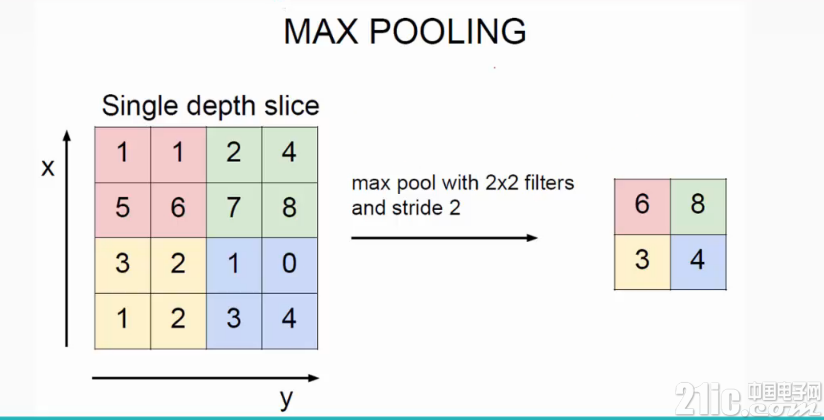
池化常用的是两种，一种是 Avy Pooling，一种是 Max Pooling。下图是 Max Pooling 的示意图，可以看到分别找的是 2*2 矩阵中的最大值，Avy Pooling 则是将矩阵所有值加起来，求平均值。