基于滑模理论的水下航行器航向控制算法研究
对于一个理想的滑模变结构控制系统,假设“结构”切换的过程具有理想开关特效(即无时间和空间滞后),系统转态测量精确无误。控制量不受限制,则滑动模态总是降维的光滑运动而且渐进稳定于原点,不会出现振抖。但是对于一个现实的滑模变结构控制系统,这些假设是不可能完全成立的。特别是对于离散系统的滑模变结构控制系统,都会在光滑的滑模面上叠加一个锯齿形的轨迹。于是,在实际系统中,抖振是必定存在的,而且若消除了抖振,也就消除了变结构控制的抗摄动和抗扰动的能力,因此,消除抖振是不可能的,只能在一定程度上消弱它。
本文引用地址:https://www.eepw.com.cn/article/201702/344563.htm
3 水下航行器航向滑模变结构控制
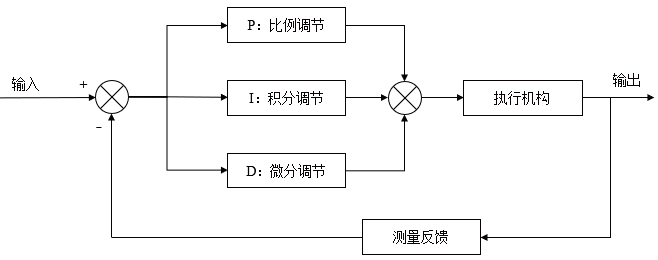
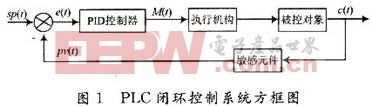
水下航行器一般是操纵方向舵控制航向,控制器根据实时传输的航向角与航向角指令值计算出方向舵舵角值,系统原理如图1所示。
在进行航向滑模控制器设计时,为了控制器设计的方便性,需要对水下航行器模型进行简化。如式(7)所示。简化的偏航方程为:


4 数值仿真研究
根据以上建立的运动学模型和控制系统,本文采用MATLAB SIMULINK对水下机器人跟踪期望轨迹进行了仿真分析。设定航速为8kn,航向角从0度到45度,仿真结果如图2所示。
从图2中可以看到稳定时间在55秒左右,最后稳态误差较小,方向舵在80秒后慢慢回零,横倾角在50秒后也慢慢回零。
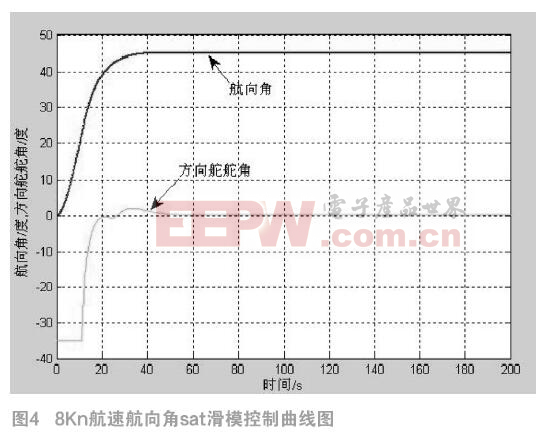
从图3中可以看出,同样设定航速为8kn,航向角从0度到45度,采用滑模变结构控制器,调节时间明显快于PID控制器,稳定时间在40秒左右,但是出现较为严重的抖振现象,采用边界层法将切换函数连续化。即用饱和sat函数代替切换函数中的sgn。饱和函数的定义为:
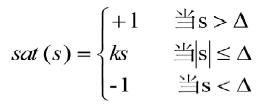 (15)
(15)
设定航速为8kn,航向角从0度到45度,仿真效果如图4所示。从图4中可以看出抖振明显减弱,控制效果良好。
5 结论
本文通过对水下航行器数学模型的分析,设计了滑模控制器,计算机仿真结果表明滑模变结构控制器对于不同航行条件具有较强的适应性,同时航向的控制效果明显优于PID控制器。
参考文献:
[1]边宇枢,高志慧,贠超.6自由度水下机器人动力学分析与运动控制[J].机械工程学报,2007,43(7):87-92.
[2]唐旭东,庞永杰,李晔.水下机器人运动的免疫控制方法[J].电机与控制学报,2007,11(6):676-680.
[3]俞建成,张艾群,王晓辉,等.基于模糊神经网络水下机器人直接自适应控制[J].自动化学报,2007,33(8):840-846.
[4]刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407-415.
[5]严卫生.鱼雷航行力学[M].西安:西北工业大学出版社,2005.
[6]李殿璞.船舶的数学建模[M].哈尔滨:哈尔滨工业大学出版社.2001.
本文来源于《电子产品世界》2017年第2期第27页,欢迎您写论文时引用,并注明出处。



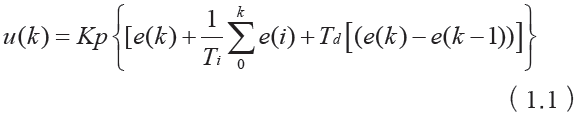


评论