生物电阻抗测量系统中弱信号检测技术研究--正交双激励信号检测方法

3.4.2.1 DPSD仿真分析

利用图3.7所示的仿真系统进行仿真，将参数设定为：输入信号一个周期的量化点数为10，输入信号的相位偏移分别为0°和45°。可得到结果如图3.10所示的仿真结果图。

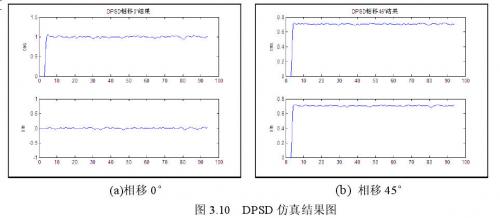
仿真结果图中，横坐标为累加的点数，纵坐标为相应的三角函数值。由图3.10的仿真结果表明，信号通过网络后，被提出来的正余弦值与设定相位的正余弦值基本一致，因此这种方法是可行的。

3.4.2.2 D-DPSD仿真分析利

用图3.8所示的仿真系统进行D-DPSD方法仿真。将参数设定为：输入信号一个周期的量化点数为10，输入信号的相位偏移分别为0°和45°。可得到如图3.11所示的仿真结果图。

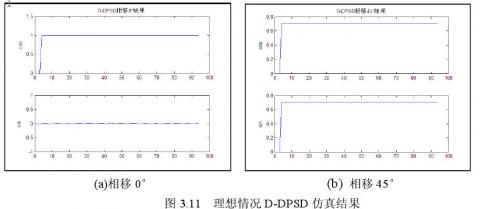
仿真结果表明，信号通过网络后，被提出来的正余弦值与设定相位的正余弦值一致，因此这种方法可以更精确的计算出信号的幅度和相位。

现实情况中，当激励信号输入系统时，往往伴有随机噪声和白噪声输入。运行图3.9所搭建的仿真系统，得到加噪情况下的仿真结果如图3.12所示。

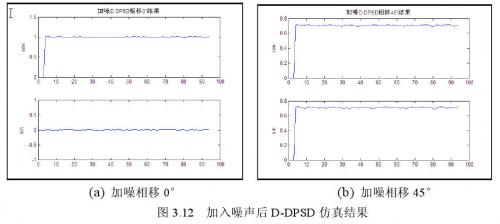
仿真结果表明，信号通过网络后，被提出来的正余弦值与设定相位的正余弦值基本一致，信号平稳，因此这种方法可以得到信号的幅度和相位。

3.4.2.3 D-DPSD与DPSD仿真分析

对比D-DPSD算法在DPSD算法基础上提出，将D-DPSD仿真结果与DPSD在相同条件下的仿真结果进行对比，如图3.13所示。由图可知，D-DPSD算法仿真结果明显平稳，误差浮动范围有所减小。因此，D-DPSD减小了DPSD算法累积产生的误差，从而使整个系统的误差得到减小，提高了系统测量信号幅度和相位的精度。

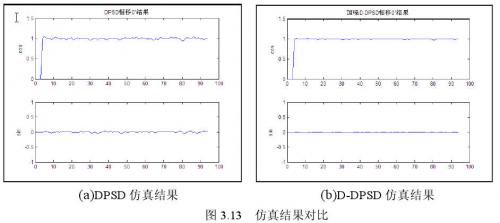
分析测量过程，测量精度主要受AD采样、乘法器截断误差以及累加器截断误差影响。只要设计采用12位以上AD进行采样，并保证差分输入峰峰值为±1.024V.可计算其量化误差为：

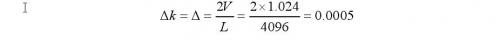
量化范围为-V到+V，L为量化间隔数。

为提高测量精度，乘法器和累加器分别采用采用24位和40位，消除截断误差的影响，这样累加器输出的结果理论误差为0.0005V，只要保证AD输入信号幅度较大，系统误差可以远小于5%，可满足生物电阻抗测量要求。