生物电阻抗测量系统中弱信号检测技术研究--EIT 中弱信号检测理论

检测中的电噪声主要是由检测系统内部噪声引起，由电阻和各种器件产生的。绝大多数的电噪声是一个连续型随机变量，是一种前后独立的平稳随机过程，在任何时刻，它的幅度、相位以及波形都是随机的，但还是服从于一定的统计分布规律。

电阻热噪声是由电阻内部自由电子的热运动而产生的。起伏电流，电阻中的带电微粒(自由电子)在一定温度下受到热激发后，在导体内部作无规则的运动(热骚动)而相互碰撞，两次碰撞之间进行时，就产生一持续时间很短的脉冲电流。许多这样的随机热骚动电子所产生的这种脉冲电流组合，就在电阻内部形成了无规律的电流。在一足够长的时间内，其电流的平均值等于零，而瞬时值就在平均值上下变动。当实际电路中包含多个电阻时，每一个电阻都将引入一个噪声源。一般若有多个电阻并联时，总噪声电流等于各个电导所产生的噪声电流的均方值相加。

2.3常用弱信号检测算法

生物弱信号的特点是幅度小，往往淹没在噪声之中。为了检测被背景噪声覆盖的微弱信号，人们进行了长期的研究工作，分析噪声产生原因及规律，研究被测信号的特点、相关性及噪声的统计特性，以寻找从背景噪声中检测出有用信号的方法。常用的微弱信号检测方法有：相干检测法、基于混沌振子的微弱信号检测、同步累积法、双路消噪法、窄带滤波法等。

2.3.1相干检测法

相关接收技术是应用信号周期性和噪声随机性的特点，通过自相关或互相关运算，达到去除噪声、检测出信号的一种技术[13][15]。由于信号和噪声是相互独立的过程，根据相关函数和互相关函数定义，信号只与信号本身相关，与噪声不相关，而噪声之间一般也不相关。

2.3.1.1自相关检测

实现自相关检测的原理框图[13]如图2.3所示。

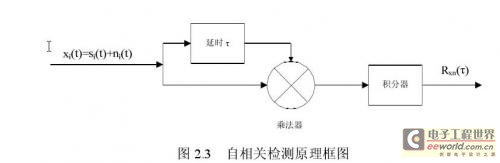
设输入x i(t)由被测信号s i(t)和噪声n i(t)组成，即：

x i(t)同时输入到相关接收机两个通道，其中一路将经过延时器，使它迟延一段时间τ。经过迟延的x i(t-τ)和未经迟延的x i(t)均送入乘法器内，再将其乘积积分，然后输出平均值，从而得到相关函数上一点的相关值。如果变更迟延时间τ，重复上述计算就能得到相关函数R xx(τ)与τ的关系曲线，即得自相关的输出为：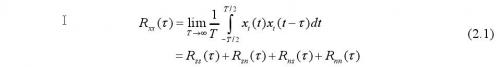

根据互相关函数性质，由于信号s(t)与噪声n(t)不相关，并且噪声的平均值为零，得到R sn(τ)=0，R ns(τ)=0，则R xx(τ)= R ss(τ) +R nn(τ)。随着τ的增大，R nn(τ)→0，则对充分大的τ，可得R xx(τ)= R ss(τ)。这样就得到了信号s i(t)的自相关函数R xx(τ)，它将包含着s i(t)所携带的某些信息。

随着时间τ的增加，噪声的自相关函数迅速衰减，而信号的自相关函数是小衰减的周期函数，从而可检测出有用信号。

2.3.1.2互相关检测

如果发送信号的重复周期或频率已知，就可在接收端发出一路重复周期与发送信号相同的本地信号，将本地信号与混有噪声的输入信号进行互相关。如图2.4是实现互相关检测的原理框图，设输入x(t)为：x (t ) = s (t ) +n (t )

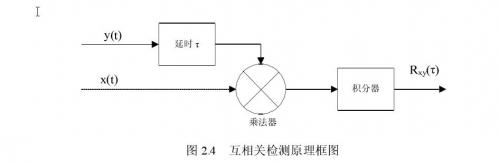
s(t)为待测信号，n(t)为信号s(t)中混入的噪声，y(t)为己知参考信号，若y(t)与信号s(t)有相关性，而与噪声n(t)无相关性，输入经延时、相乘、积分及平均运算后，得到互相关输出R xy(τ)为：

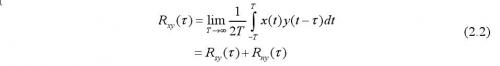
由于参考信号y(t)与信号s(t)有某种相关性，而y(t)与噪声n(t)没有相关性，且噪声的平均值为零，则有R ny(τ)=0，即：

根据互相关函数的性质R xy(τ)中包含了信号s(t)所携带的信号，从而将待测的信号s(t)检测出来。

2.3.2基于混沌振子的微弱信号检测

混沌理论作为一门新学科已经引起了大家的重视，是近年来非线性科学领域的热门学科。混沌目前尚无通用、严格的定义，一般认为，在某些确定性非线性系统中，不需要附加任何随机因素，仅由其内部存在着非线性的相互作用所产生的类随机现象称为混沌。当系统发生混沌行为时，系统响应对系统参数由噪声产生的摄动并不敏感，也就是系统的混沌行为对噪声具有一定的免疫力，这类非线性系统行为对参数的依赖性和混沌吸引子对噪声的免疫力使其在微弱特征信号检测方面具有潜在的应用前景。在许多工程实际中，微弱特征信号的产生就表明系统的运行状态发生了变化，如何检测这些在强噪声干扰情况下的微弱信号是信号处理中的重要研究内容。

目前混沌振子用于微弱信号检测的研究己经越来越深入。混沌振子由于参数的不同会表现出不动点、周期、拟周期、混沌等动力学状态。对两种状态的相互转换时的参数临界值，在非线性科学中称为“分叉值”，两种状态间的转换称为“分叉”。Duffing振子信号检测技术主要是利用混沌系统的分岔特性来检测外界信号，将待测信号作为Duffing方程周期策动力的摄动，利用初值敏感性可以获得很高的测量灵敏度和良好的抗噪性能。

利用混沌振子检测微弱信号的方法就是将一个非线性含参数系统设定在其参数的临界值附近，微弱的特征信号作为对分叉参数的摄动，当具有某一微弱的特征信号作为摄动项加入系统时，则非线性系统的定性状态就会发生变化。通过对非线性系统的定性状态有无发生变化进行判别，进而达到检测微弱特征信号的目的。

由混沌理论知：一类混沌系统在一定条件下对小信号具有敏感性，同时对噪声具有免疫力，因此使得它在信号检测中非常具有潜力。由非线性理论知：对于一个非线性系统，当其敏感参数在一定范围存在摄动时，将引起其周期解发生本质变化。由此，可以利用非线性系统的周期解所发生的本质变化来检测微弱信号。

当采用Duffing振子作为非线性系统来检测微弱信号时，让Duffing振子处于混沌和周期解之间的临界状态，将待测信号作为Duffing振子周期策动力的摄动，通过Duffing振子对噪声和目标信号的不同反应来检测目标信号。当待测信号经过Duffing振子时，噪声虽然强烈，辩识系统状态，可以清楚地检测出特定信号是否存在。

利用混沌振子方法可以从很强的噪声信号中检测其中的特征信号是否存在，该方法具有巨大的应用潜力。但这种方法也存在一定的缺陷：

1.若系统输出本来就是稳定周期状态，但由于无法事先知道，所以只能通过观察相图，最终证明输出是稳定状态，那么这种判别方法的工作效率是比较低的。

2.根据系统的相轨迹图来判别系统的状态，即系统是处于混沌状态还是已经跃变到了周期状态，也是不够准确的，容易出现误判。这种判别方法虽然简单、直观，但终归是一种人为的识别方法，所以没有一个严格意义下的数学判别标准，缺乏理论依据。

2.3.3同步积累法

同步积累法的原理是利用信号的重复性和噪声的随机性，对信号重复测量多次，使信号同相的积累起来。噪声则无法同相积累，使信噪比得到改善。在这种方法中，测量次数越多，则信噪比改善越明显。

若测量次数为n，则积累的信号为：

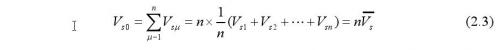
其中，

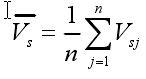
为累积信号的平均值，实际上等于输入信号V si。另一方面，重复测量n次后，根据各次噪声的不相关性，则积累的噪声等于：

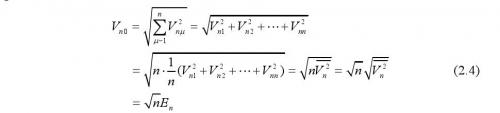
上式中最后的E n为累积噪声的均方根值。

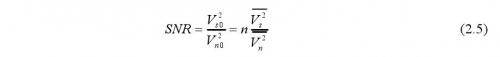
得到信噪比为：因此，测量次数n越大，则信噪比的改善越明显。而增加测量次数，就意味着延长测量时间，所以信噪比的改善是以耗时间换来的。