测量数据舍入算法
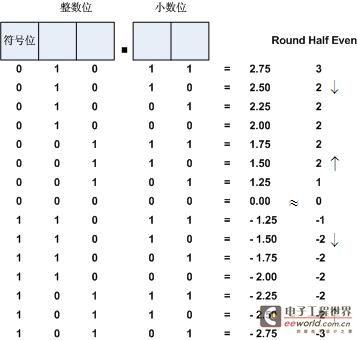
图5
(4). Round Half Odd
Round Half Odd算法根据有效位来判断是否进位,在此例中,舍去小数位,因此判断整数位即可,如果整数位为奇数,则不进位,偶数则进位,因此舍入处理后整数位肯定是个奇数。如图6所示,可以发现Round Half Odd必然是Symmetric算法。
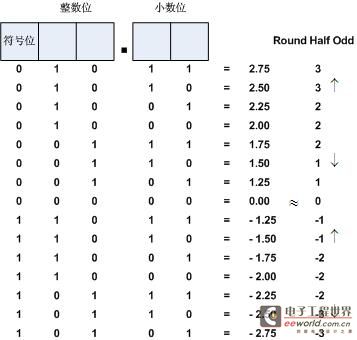
图6
Round Ceiling
Round Ceiling算法的舍入处理总是朝正无穷趋近,对于正数而言,只要舍去位大于0,就进位;对于负数则直接截断处理,如图7所示。
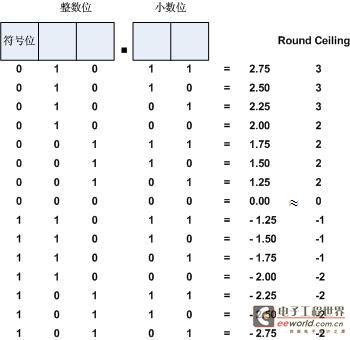
图7
Round Floor
Round Floor算法的舍入处理总是朝负无穷趋近,舍入处理与Round Ceiling相反,对于负数而言,只要舍去位大于0,就进位;对于正数则直接截断处理,如图8所示。
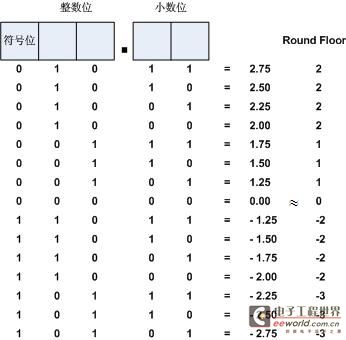
图8
Truncation
Truncation是直接的截位处理,如图9所示。另外还有一种Round To Zero算法,舍入处理采用的也是简单的截断。
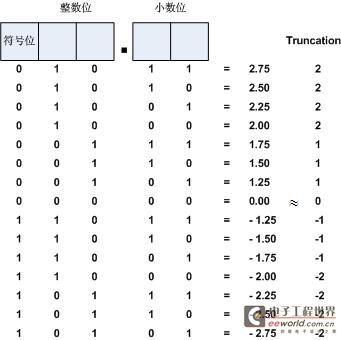
图9



评论