一种基于移动基站的无线传感器网络数据收集方法

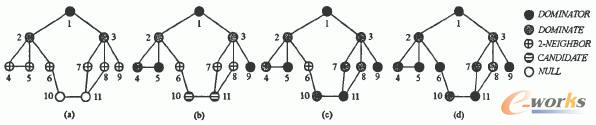
图3 构建支配集的分布式算法简单示例

2．3路径优化

确定支配集后，基站还需要获取各个节点的位置信息，选择经过这些节点的一条较短的路径。在支配集构建时，可以将基站置于网络中任一节点处，并从该节点开始分布式算法，发送角色消息的同时在消息内包括从开始节点计算的跳数，从而可以不付出额外的通信代价建立起任意节点到开始节点的最短路径路由。各个DOMINATOR节点可以在确定自己的角色后通过多跳路由将位置信息传递回基站。此时，就可以将路径优化问题转换成旅行商问题，寻找一条最短的圈且经过每个点仅一次。然而，旅行商问题也被证明为NPhard问题。本文中使用kahng等提出的一种近似算法。该算法使用两次连续的匹配来选择完全图中的一部分边来将所有必须访问的位置连接起来。第一次匹配选择具有最小权重(本文中使用欧氏距离作为权重)的边，是每个位置仅与一条边相关联。在将这些边从图中清除后再进行第二次匹配。两次匹配所选择的边构成多个圈。然后。再将这些圈连接成一个大圈，即为算法的结果。在下一节中，我们将给出基于上述算法的仿真结果。

3 仿真评估

本节中，我们提供了支配集构建和路径优化的仿真结果，并将本文的方法和基于树形结构的收集方法的负载分布也通过仿真进行了比较。在仿真设置中，选择了500×500单位长度的正方形区域作为传感器网络的部署区域。假定传感器的传输范围是圆形区域，通信半径为r=50。

使用支配集的势和所需使用的消息总数作为指标，首先将2．2节中的算法与Wan等提出的算法进行了比较。在基本场景中，我们使用1000个随机分布的节点。通过改变节点数量使其从500变化到2000，模拟节点密度的变化。在每个场景下，我们进行10次仿真并取平均值作为实验结果。实验结果如图4所示。在图4(a)中，我们提出的算法所生成支配集的势比较稳定，而Wan等所提出算法的结果则随着节点数目的增加而略有增加。我们的结果具有更小的势，仅为Wan等结果的50％～60％。在图4(b)中，两种算法的通信消耗都随着节点数的增加而线性增长。我们的算法仅需要约占Wan等提出算法的50％的代价。我们的算法在支配集的势和通信消耗两个方面都优于Wan等提出的算法。随后，分别基于上文中两种算法的结果，使用kahng等提出的算法生成移动路径。同样改变节点数量从500到2000。在每个场景下，进行1O次仿真，并使用平均值进行比较。仿真结果如图5所示。两条曲线都随着节点数的变化而波动，其原因是拓扑结构是随机生成的，各个拓扑可能有不同的性质。但使用我们算法的结果要优于使用Wan等所提出算法的结果，即减少支配集的势确实有助于缩短移动路径的长度。

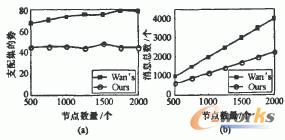
图4支配集的势和通信代价比较

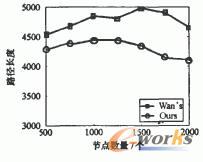
图5 移动路径的长度

我们分别对本文的方法与使用树形结构且静态基站位于网络中心的方法进行了仿真。仿真使用了具有2500个节点的网格拓扑。两种方案都需要构建最短路径树作为路由。此处我们忽略了构建最短路径树的通信消耗，而只考虑数据收集过程中的消耗。图6显示了我们提出的方案和基于树形结构收集方案在一次性收集所有节点上数据时的负载分布。其中X、y分别表示二维平面的坐标轴，使用基于树形结构的收集方法时，基站位于网络的中心位置。很容易看出我们的方案仅有极低的通信消耗且具有更均衡的负载分布。在图6(a)中，所有节点所需发送的消息数都不超过5，而在图6(b)中相当一部分节点需要发送超过100个消息。在图6(b)靠近中心位置处，有的节点需要发送的消息个数远远超出其他节点。正是这些节点的寿命限制了网络寿命。仿真结果显示我们的方案具有很好的可行性。与基于树形结构的收集方法相比，它具有低通信消耗和更平衡的负载分布。我们的方案不需要转发别的节点生成的数据，因此明显比其他联合使用移动基站和多跳路由方法更高效。

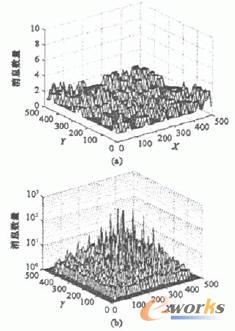
图6 本文提出的方法和基于树形结构收集的负载分布

4 小结

我们提出了一种基于移动基站而不使用多跳路由的数据收集方法。该方法结合了支配集相逢算法和旅行商问题的近似算法。仿真结果显示，所提出的支配集构造算法具有更低的通信消耗和更低势的支配集结果，并能生成更短的移动路径。所提出的数据收集方法还具有负载均衡分布的特性。此外，该方法不使用UDG等理想状态模型。从而具有很好的实用性。