噪声调频信号检测方法

　　当白噪声累加到调频干扰后在得到的功率谱，如图2所示。

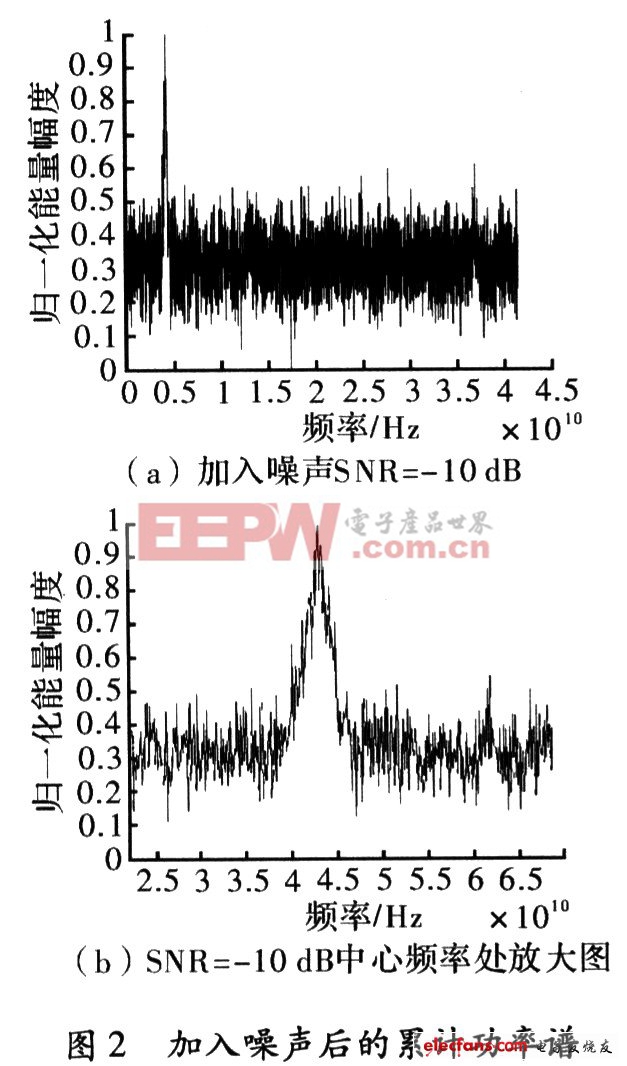
　　从图2中可以看出在SNR=一10 dB情况下，可以检测处噪声调频干扰信号，且在中心频率处的能量有所衰减。由于考虑仿真速度的需要此处所取时长较短，如果加长时间的积累，即相当于增加了能量的积累，得到的检测灵敏度会更高。对于检测门限的设定，是在实际应用中关心的问题。这里简述两种参考门限的确定方法。第一，对于系统的热噪声是在设计时所确定的固有性质，相对外界环境要稳定的多，在设置门限时可以考虑当切断外来所有的信号输入，得到的机内热噪声的功率均值数作为参考门限，这样的好处是确保此时噪声纯净，缺点是没有考虑环境噪声的存在，从而出现虚警的概率增加，这也是文中使用的方法;第二，是在侦察天线没有对准干扰源的情况下，得到内外混合噪声的各个频点的功率均值作为参考门限，其优点是能够真实的反映实际情况，但是如果此时有其它发射机信号的输入，则检测出现漏警的概率会大大增加。

　　2 相似理论

　　在信号与系统学科中，相关性是一种在时域中对信号特性进行描述的重要方法。由于信号与其功率谱函数是一对傅里叶变换，在信号分析中往往利用它来分析随机信号的功率谱分布，以致不少人一提到相关性马上会联想到信号功率谱的计算。假设得到的两信号分别为X(t)，Y(t)。可以选择当倍数K使KY(t)去逼近 X(t)。在此可以借用误差能量来度量波形的相似程度。

　　其中Er代表误差能量，K的选择是为了使误差能量最小，可以得出

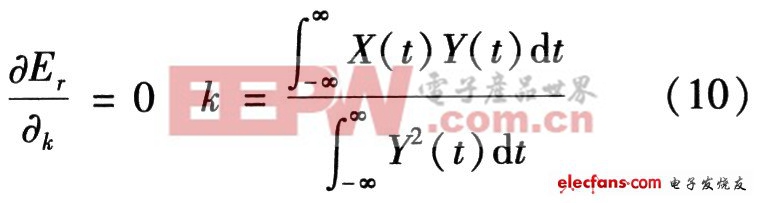
　　另外，可定义相对误差能量为

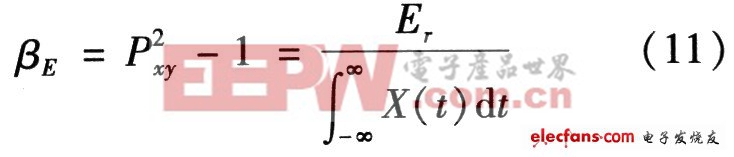
　　其中Pxy为相关系数。可以推出

　　对于能量有限的信号而言，能量是确定的，相关系数的大小只由X(t)*Y(t)积分决定。若两个完全不相似的信号，其幅度取值和出现时刻是相互独立、彼此无关的，即X(t)*Y(t)=0，其积分结果也为0，所以当相关系数为O时相似度最差，即不相关。当相关系数为1时，则误差能量为0，说明这两个信号相似度很好，是线性相关的。因此把相关系数作为两个信号相似性的度量完全是有理论依据的、合理的。

　　3 利用相似理论的噪声调频信号检测

　　为了讨论方便，假设接收机为理想接收机，即在通带内，其幅频特性为一固定值，相频为线性，而通带之外增益为零，中心频率ω0为且远大于接收机带宽△ω，并假定背景噪声是高斯白噪声，这种假设不失一般性，基本可以很好地描述常规接收机的检测特性。

　　在时长1 ms，信噪比从一10～10 dB进行100次蒙特卡洛实验，其信号具体形式如第2节所述，首先得到信号和基准白噪声的各自的功率谱，然后代入式(12)中，计算其相关系数。考虑到虚警的可能性，通常认为当相关系数0.8时存在噪声调频干扰，否则没有噪声干扰信号进入。所得结果，如图3所示。

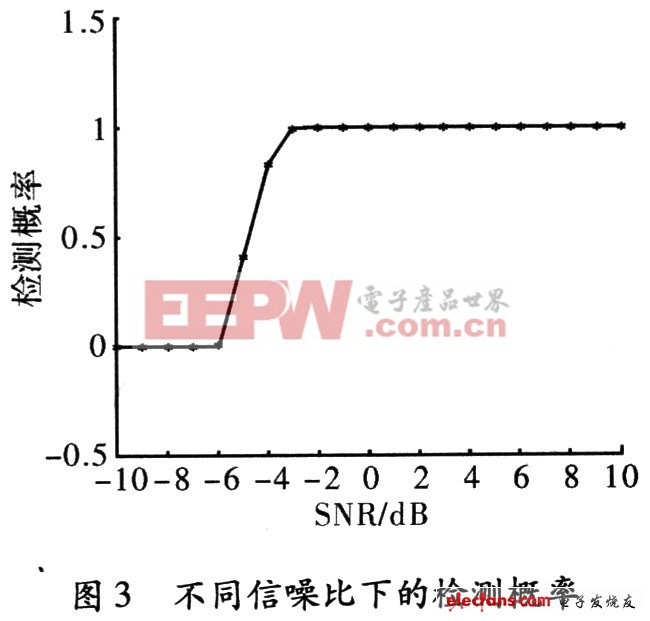
　　从图3可以看出在信噪比一3 dB以上能够在时长0.1 ms下做到100%的检测。充分说明了该方法对检测识别噪声调频信号是可行的。而且根据积累时长的不同，对算法检测的灵敏度影响很大，在图4给出了不同积累时间10次蒙特卡洛实验的检测概率。