基于变结构混沌的伪随机序列发生器

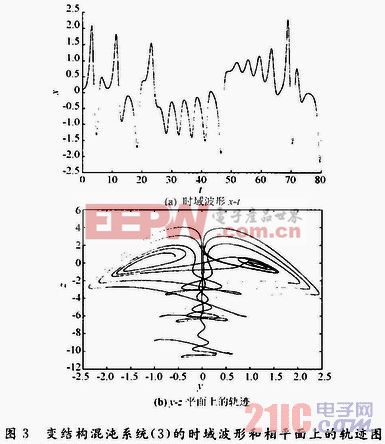
图3中，实线和虚线分别为为系统(1)和(2)的波形或轨迹。
从图3看出，该系统的信号波形或解的轨迹由两个不同的部分构成。当系统的解x≥m=0．2时，u(x-m)=1，混沌系统(3)为混沌系统(2)的结构；当系统的解xm=0．2时，u(x-m)=0，式(3)变为混沌系统(1)的结构，如此往复变化。虽然在这种结构变化中的门限为一确定值，但由于混沌的不可预测性导致何时达到这一门限足无法预知的，即这种结构随时间而变化的规律是无法预知的，也是随机的。
这种由两个不同的混沌信号按时间随机地混杂在一起而形成的一个完整的混沌信号，比之由单一混沌系统产牛的信号要复杂得多，且门限参数本身又是一种密钥参数，它扩展了混沌伪随机序列的密钥空间，使其提高了安全性。

2 伪随机序列发生器设计及性能分析
基于上述的变结构混沌系统可设计一种新的伪随机序列发牛器。主要思路是以变结构混沌系统作为随机信号源，采用一定的方法对其离散、量化，获得一系列的伪随饥序列。
这里研究的变结构混沌系统是一个非线性常微分方程组，在数字系统中对其进行数值解就是一种离散的方法。常微分方程近似求解的数值方法有欧拉算法、改进型的欧拉算法和龙格库塔法等，这都是将连续系统进行近似离散化的方法。其中，欧拉算法速率最快，本文采用欧拉算法将连续混沌离散化。对于一个连续的混沌系统，有：


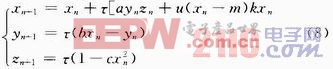
当τ足够小时，经过欧拉算法离散化后的系统具有与式(3)所示的连续混沌系统相同的动力学特性，此处选择τ=0．004。
在数字系统中迭代求解式(8)所示的离散化系统，迭代过程中的每一个解变量xn，yn和zn都可以通过二进制数据的方式来表示。以xn为例：

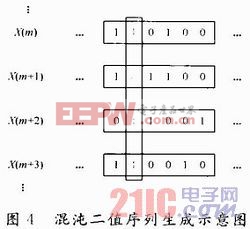
式中：b1n，b2n，…，b(k+1+l)n分别为二进制数的所有位(0或1)，混沌系统的解xn随时间不断变化，其二进制表达式中的每一位bm(“0”或“1”)也随时间小断变化。如果抽取随时间变化的一位或多位，可构成一个由“0”或“1”组成的伪随机序列。为了保证提取的序列具有较好的随机性，可以严格地从小数部分中提取其中一位作为随机序列，也可以从{b1n，b2n，…，b(k+1+l)n}中选取随机性能较好的多位作为随机序列，从而增加随机序列的提取速度。这种量化方法可用图4表示。