基于Toeplitz方程的改进广义预测PID控制
PID参数设计
3.1广义预测模型描述
广义预测控制采用如下离散差分方程描述,也即CARIMA模型:
(12)
使用如下的Diophantine方程

3.2PID和GPC的结合
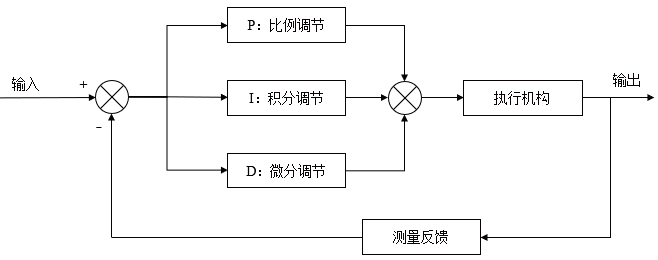
PID控制的具体算法为:它根据给定值r(t)与实际输出值y(t)构成控制偏差,然后将偏差的比例(P)、积分(I)、微分(D)通过线性组合构成控制量,对被控对象进行控制,如下式所示:

(23)
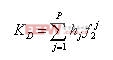
实验仿真及结果分析
选择一个仿真模型,如下:
运用同样的参数,传统PID算法和改进的GPC-PID算法仿真结果如下图表示。其中,红色曲线代表传统PID算法,蓝色曲线代表改进的GPC-PID算法。
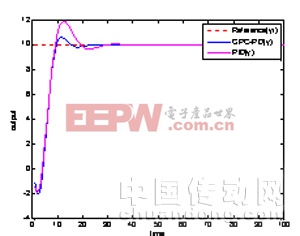
图1-控制输出
从图1中可以看出本文使用的GPC-PID预测算法比传统的PID控制器更加平滑,新的预测算法所需用的时间比传统算法更快达到稳定,基于Toeplitz的矩阵很好的展现了这一特性,节省了在线计算的时间,而传统算法则不具备这一优点。本文引用地址:https://www.eepw.com.cn/article/186997.htm
方法 | 在线计算时间 |
传统PID算法 | 0.11068s |
本文方法 | 0.05749s |
表格1-计算时间比较
从这个表格中可以看出改进的GPC-PID算法所用时间更短,并且输出的波动明显降低。改进算法在线计算时间更短,很好的减少在线求解G潘图方程的复杂程度,减轻了系统的负担。最后的曲线也更加平滑,达到了预期效果。
结语
PID控制技术是目前应用最广泛的控制技术,本课题在保证经典PID控制性能发挥其简单实用长处的基础上,根据滚动优化原理整定PID控制参数。所提出方法,避免了已有预测PID控制方法需要递推求解Diophantine方程的弱点,提高了预测PID算法的运行速度,从而也拓宽了算法的工程应用范围。





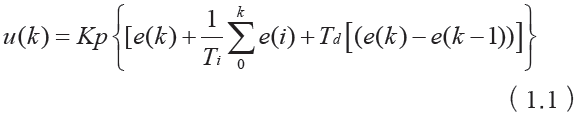
评论