基于CVCF逆变器的波形控制技术设计
取电容电压vC和电容电流iC作为状态变量,PWM逆变器的空载模型为:
![]()
引入状态反馈
其中r 是闭环系统参考指令,K是反馈增益阵,则闭环系统的状态方程变为:
将闭环极点配置在z域的0.74±0.3i点,此时系统自振荡频率ωn为4454rad/s(大致与LC滤波器截止频率相同);阻尼比ξ为0.5.图 5(a)是系统的突加负载仿真波形,观察发现输出电压在突加瞬间跌落后不能完全回到原来的轨迹,而是有一个固有的静态误差。对反馈系统分析发现,电容电压vC 反馈相当于一个比例环节P,电容电流iC 反馈相当于一个微分环节D,都不能消除静态误差。因此,我们在控制系统中引入积分环节,把输出y的积分量和状态变量一起作为反馈量,假设这个新变量为xI,即
原来的二阶系统变为了三阶系统

新增一个配置极点在z域的0.1,此时系统的突加负载仿真波形如图5(b)所示,我们可以看见原有的静态误差已经被消除。
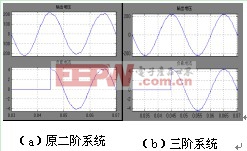
图5 突加负载仿真对比
复合控制
综合以上两种控制方案构成整个控制系统,其中,状态反馈极点配置控制居于控制系统内层,其目的是通过重新配置极点来改善系统的动态响应特性。重复控制居于控制系统外层,其主要目的是减小非线性负载等因素造成的谐波失真。只要极点配置和重复控制单独作用时系统稳定,那么复合系统就是稳定的。 实验结果
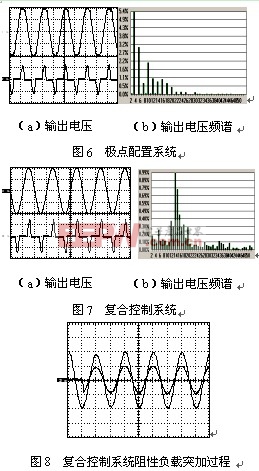
图6是极点配置系统带整流型非线性负载的波形,THD值为6.89%.图7是加上外层的重复控制后的非线性负载工作波形,负载电流峰值15A, THD值降为1.42%,分析电压频谱发现13次以下的谐波幅值有明显的衰减,这验证了重复控制的谐波抑制能力主要体现在中低频段。图8是复合系统突加 5A的阻性负载电压波形,系统很快结束过渡过程,同时也基本消除了静态误差。
结论
本文分析了重复控制和极点配置两种控制方式在数字化CVCF逆变器中的应用,提出了一种基于重复控制和极点配置的复合控制策略。实验结果证明该策略使系统得到了比较理想的稳态特性和动态特性,而且易于实现,有一定的实用价值。





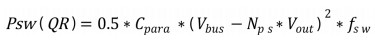





评论