终于有人把线性回归讲明白了（2）

03 线性方程的“直男”本性

也许你对名为“模型”的大盒子充满期待，同时又担心会冒出一大堆数学符号，所以不敢马上掀开一窥究竟。不过，线性模型反倒更像是一个过度包装的大礼盒，大大的盒子打开一看，里面孤零零只有一样东西：线性方程。第一次接触时各种名词很容易把人绕糊涂，不急，我们先把名词之间的关系捋一捋。

前面在介绍机器学习的基本原理时，提到“假设函数”这个术语，假设函数是一类函数，所起的作用就是预测，这里的线性方程就是线性回归模型的假设函数。

别看名字挺“高冷”，其实特别简单。“线性”就是“像直线那样”，譬如线性增长就是像直线那样增长。我们知道，直线是最简单的几何图形，而线性方程说直白一点，就是能画出直线的一种方程。如果方程有性格的话，那么线性方程一定就是“直男”的典型代表。

直线方程最大的特点就是“耿直”，由始至终都是直来直去，函数图像如图3-4所示。

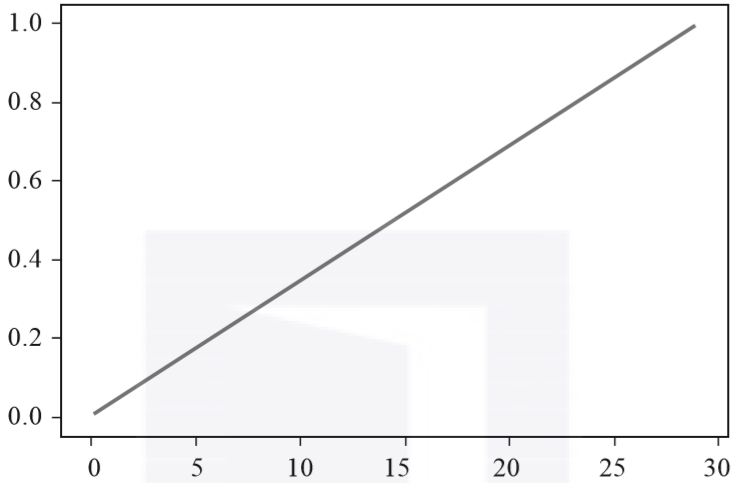
▲图3-4 线性函数的函数图像

这样看好像也没什么，但对比一下同样常见的以2为底数的对数函数（见图3-5a）和指数函数（见图3-5b）就能明显看出，其他函数多多少少都要带一点弧度，这是变化不均匀所导致的。相比之下，直线方程开始是什么样子则始终是什么样子。

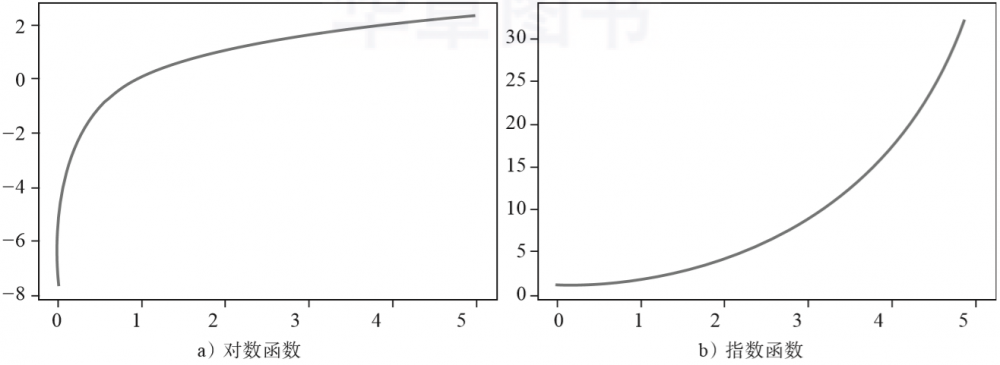
▲图3-5 非线性函数的函数图像

直线方程通常写作y=kx+b，k称为斜率，b称为截距，这两个参数可以看作两枚重要的旋钮，直接控制直线进行“旋转”和“平移”的动作。具体来说，通过调整斜率，可以改变直线的角度。

在图3-6的四幅图中，直线均具有相同的截距，黑实线斜率均为2，但右上、左下、右下的三幅图中灰线斜率分别为1、1/2和0，对比黑实线可以看出，通过改变斜率可以使直线出现“旋转”的动作效果。

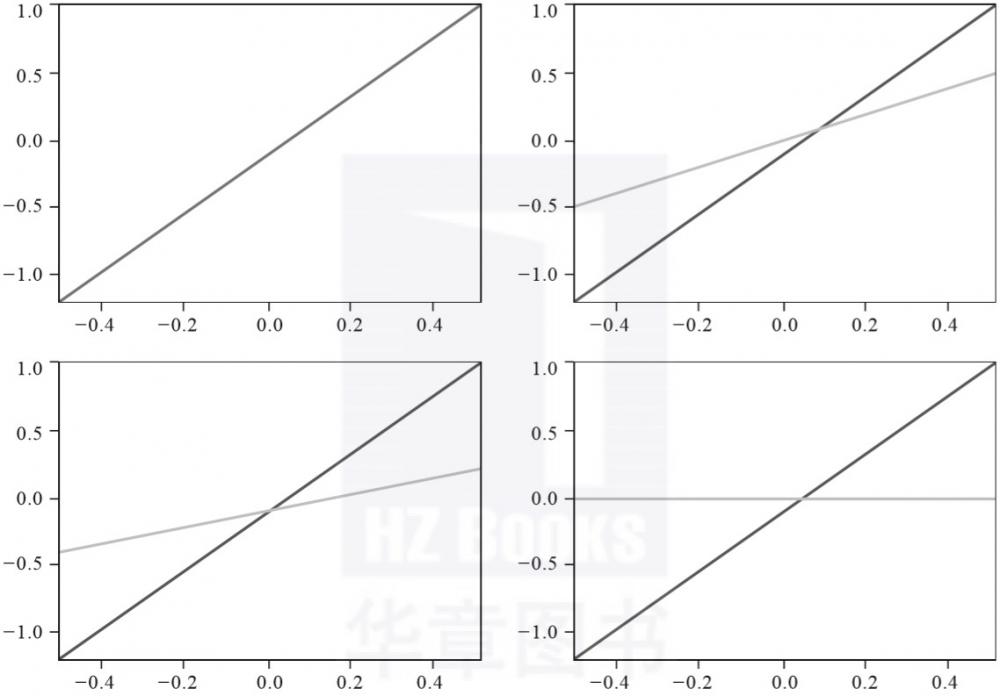
▲图3-6 4条斜率不同的线性函数图像对比

直线还有另一种调节方法。通过调整截距b，可以实现直线的上下平移。如图3-7所示，这三条平行的直线具有相同的斜率，但截距相差1，可以看到直线出现了上下平移的动作效果。

“旋转”和“平移”就是直线的全部看家本领了，这正体现了线性方程简单直率的“直男”本性。

准确来说，线性方程和直线方程还是存在一点微小差别的。直线是二维平面图形，而线性所在的空间则可能是多维的。不过，无论是在二维平面还是在多维空间，直线所能做的也就是“旋转”和“平移”两套动作，线性模型想要拟合能够调节的参数，主要也就只有这两个。

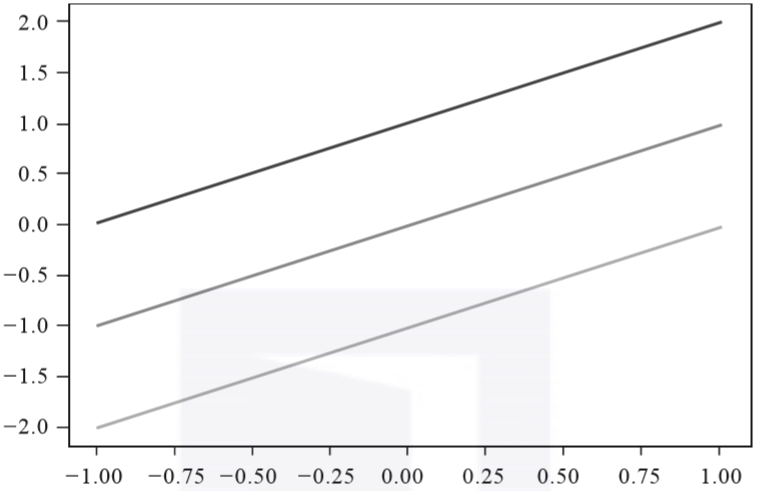
▲图3-7 三条截距相差1的线性函数图像对比

在机器学习中，斜率k通常用字母w表示，是权值（weight）的首字母。通过调整w和b的值就能控制直线在多维空间中进行旋转和平移，扮演的角色很像老式收音机上的旋钮，通过旋转旋钮就可能收听到想要的电台。

这个通过调整权值来达到目的的过程叫作权值调整或者权值更新，对于线性模型而言，学习过程的主要工作就是权值调整，只要旋动旋钮，合理搭配旋转和平移这两套简单的动作，就能完成对输入数据的拟合工作，从而解决回归问题。

关于调整权值的另一种解释

在机器学习中，通过调整权值来完成学习，并最终进行预测的算法很多，这也是一种非常常见的学习手段。对于为什么调整权值能够进行预测，实际上也有多种解释，上面从几何角度给出了解释，此外还有代数角度的解释。

以三个输入维度A、B、C来预测P为例，我们的线性方程可以写为：

F=W1*A+W2*B+W3*C

假设我们知道P的值其实就是与A的值有关，与B、C毫无关系，那么，怎样调整线性方程才可以根据输入准确预测出P的值呢？

我们知道，线性方程的计算结果F是三个维度的加权和，想要使F与P最接近，只需要让线性方程中B、C这两个加项对结果影响最小即可。这个好办，只要使这两项的权值最小，也就是W2和W3的值为0就可以了。

这就是从代数角度来解释为什么调整权值能够提高预测结果的准确性。这里实际上体现了一种假设，就是待预测的结果与输入的某个或某几个维度相关，而调整权值的目的就是使得与预测结果相关度高的权值越高，确保相关维度的值对最终加权和的贡献越大，反之权值越低，贡献越小。

04 最简单的回归问题——线性回归问题

前面我们介绍了什么是回归问题，也直观感受了线性方程的“直男”本性，那么在这一节将对为什么模型能进行预测给出一个很直接的回答。当然，学术界对于这个问题的认识还未完全统一，这里选择沿用一种当前最主流的观点。

直到目前为止，我们还不能全面地了解这个世界，但纷繁复杂的现实世界大体还是遵循着某种规律的，我们不妨叫作“神秘方程”。而我们在机器学习领域所做的，就是通过历史数据训练模型，希望能够使我们的模型最大限度地去拟合“神秘方程”——一旦偷看了导演的剧本，还怕有什么剧情不能预测吗？

不过，也许你已经发现，这存在一个问题。

就拿线性模型来说吧，线性模型是用直线方程去拟合数据，但直线可是“钢铁直男”，它的动作也只有两套而已啊！模型的能力是有上限的，能力跟不上，想最大限度地拟合也还是心有余而力不足。

所以，选择模型的关键不在于模型的复杂程度，而在于数据分布。你也许会担心，线性模型简单好懂，这也是它为什么特别适合用来做入门任务，但唯一的问题是它太简单了，现实世界这么复杂，它真的能够解决问题吗？

要知道尺有所短，寸有所长，回归问题是一个大类，其中有一类问题叫线性回归问题，遇到这种问题不用线性模型还真就不行。下面，我们就来看看线性回归是怎样完成预测的。

利用线性回归进行预测的极速入门

在线性回归问题里，所要预测的“神秘方程”当然也是线性方程。这类方程存在固有特征，最明显的就是数据集点沿线性分布，所以用线性模型效果最好。也许你不敢相信，这个世界这么复杂，真的有这么简单的“神秘方程”吗？真的有，而且你肯定还见过，一起来回忆一下：

已知小明前年3岁，去年4岁，今年5岁，请问小明明年几岁？

首先这无疑是个预测连续值的问题，明明白白是一个回归问题。回归关注的是几个变量之间的相互变化关系，如果这种关系是线性的，那么这就是一个线性回归问题，适合用线性模型解决。我们按照机器学习的习惯，把已知条件整理成数据集，这是一个三行两列的矩阵：

[[2017，3],

[2018，4],

[2019，5]]

这是一个二维矩阵，如果画出图像，两个维度之间的线性关系就一目了然。这里以年份为X轴、年龄为Y轴将记录的数据画出来，得到3个呈线性排列的数据点（见图3-8a）。把这些点用线段连接起来，就能更清楚地看到这3个点排成了一条直线（见图3-8b）。

这条直线写成线性方程就是y=x-2014，即所谓的“假设函数”。线性回归的预测就依赖于这条方程，2019年刚刚过去，我们当然只能知道2019年之前的真实数据，但对于未来也就是小明在2019年之后的年龄，通过这条线性方程即可以预测得到。

譬如把“2020”作为x输入，就能计算出对应的y值是“6”，也就得到了2020年小明将是6岁的预测结果。这个例子很简单，但已经完整地展示了线性回归“预测魔力”背后的原理，线性回归的预测魔力还经常被运用在经济和金融等场景，听起来更高端，不过就原理来说，也只是这个简单例子的延伸和拓展。

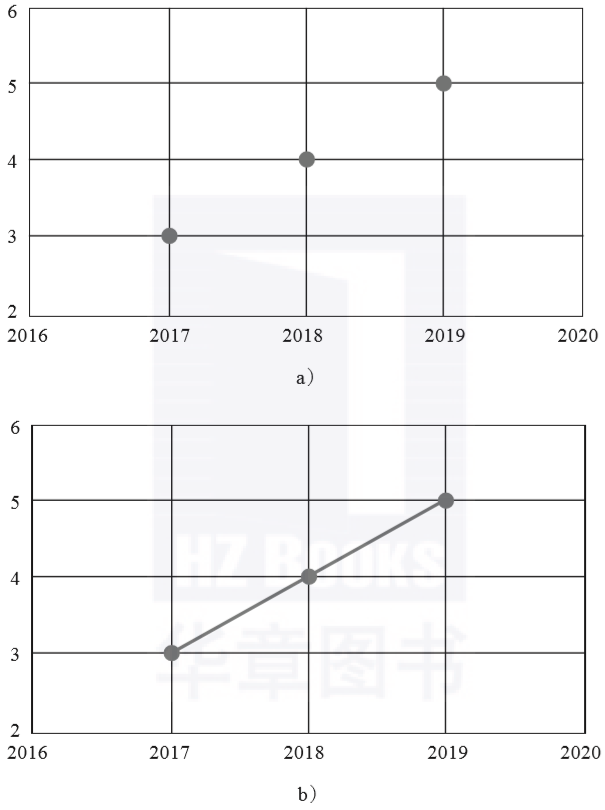
▲图3-8 呈线性关系的数据集点分布（a），如果连起来会出现一条直线（b）

关于作者：莫凡，新技术深度爱好者，曾经从事信息安全前沿技术跟踪研究和数据分析工作，在各类信息安全类技术期刊发表文章五十余篇，现转为投身高端知识“白菜化”项目，希望能让将更多听起来高大上的名词沾一沾“人间烟火”，成为日常生活中真正用得上的知识。

本文摘编自《机器学习算法的数学解析与Python实现》，经出版方授权发布。以下文章来源于大数据DT ，作者莫凡