腾讯AI Lab联合清华、港中文，万字解读图深度学习历史、最新进展与应用（2）

二、图神经网络的研究进展

了解了 GNN 的基本知识和发展脉络，接下来我们将踏入当前的前沿研究领域，解读近期的一些理论研究成果和设计创新。

1.图神经网络的表达能力

我们知道图在表达事物的关系方面能力非凡，但图神经网络表达能力的极限在哪里？清华大学计算机系助理研究员、清华大学「水木学者」、腾讯「犀牛鸟访问学者」黄文炳在课程中介绍了相关的研究进展。

为了有效地评估 GNN 的表达能力，首先需要定义评估标准。目前来说，可通过三种典型任务来进行评估：图同构、函数近似和图检测/优化/评估。

对于图同构任务，GNN 的目标是确定任意给定的两个图是否同构。这是一个很重要的任务。对于图分类任务而言，如果两个图是同构的，则 GNN 需要为这两个图输出同样的标签。

但是，判定图是否同构的问题是一个 NP-hard 问题，传统的 Weisfeiler-Lehman（WL）测试方法除了少数图结构外，基本能否识别大多数图结构是否同构。而 GNN 能更好地解决这一问题吗？

并不一定。2019 年，Xu et al. 和 Morris et al. 已经证明 GNN 至多做到与 WL 测试一样强大。之后，Xu et al. 还进一步证明，如果 GNN 中的聚合和读出函数（readout function）是单射函数，则 GNN 就与 WL 测试等效。

对于函数近似任务，该任务的目标是判断 GNN 能否以任意准确度近似任何基于图的函数。因为 GNN 本身也是基于图的某种函数，因此 GNN 在这一任务上的表现将能体现其能力。实际上，DNN 也有类似的评估任务。我们知道，只要隐藏单元足够多，DNN 可以收敛到任何向量函数，这就是所谓的「通用近似定理」。所以我们很自然也会为 GNN 提出类似的问题。

Maron et al. 提出了一种架构，对于拥有图不变映射层（graph invariant layer）和图等变映射层（graph equivariant layer）的 GNN，如果在一个非线性层（比如 ReLU）之后堆叠等变映射层，层层叠加，然后在最后添加图不变映射层。可以看出这样的模型能在输入的排列方式变化时保持映射不变性。这样的模型被称为图不变网络（INN）。

INN 有多强大？Maron et al. 证明对于任意连续的不变式图函数，如果某些条件成立，我们可以找到特定的 INN 参数，使其能以任意精度估计该函数。这是图学习领域一大强有力的理论结果。对 GNN 而言，这就相当于对 DNN 而言的通用近似定理。

看过了图同构和函数近似的近期进展，更进一步，这两者之间又有何关系呢？Chen et al. 2019 证明在满足一些条件的情况下，这两者其实是等效的。

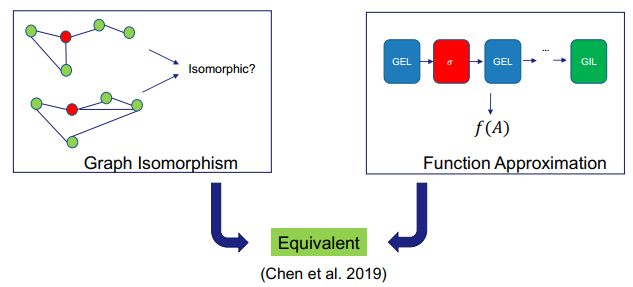
接下来，我们看看 GNN 是否有足够的表达能力来解决更困难的任务，比如寻找图中的最短路径或确定图中是否存在环。这些任务的难度很高，因为它们需要在节点层面执行很细粒度的推理。

Loukas 证明 GNN 能解决这些任务，他得出结论：只要 GNN 的深度和宽度足够，而且节点之间具有可互相判别的属性，则 GNN 就能完成这些任务。这里深度是指 GNN 的层数，宽度则是指隐藏单元的维度。

因此，总结起来，只要架构合适，GNN 其实具有非常强大的表达能力；也因此，要充分发掘 GNN 的真正实力，我们还需要更多架构方面的研究探索。

2.训练深度图神经网络

前面已经简单提到，深度对 GNN 的能力而言是非常重要的。这一点在深度神经网络（DNN）上也有体现——更深的网络往往具有强大的表达能力，可以说深度网络就是当前的人工智能发展热潮的最主要驱动力之一。

那么，具体来说，更深度的 GNN 是否也有如此的优势呢？更深度的 GNN 能否像 CNN 一样获得更大的感受野？

答案当然是肯定的。举个例子，寻找最短路径问题需要非常深的感受野来寻找所有可能的路径，环检测和子图查找问题也都需要较大的感受野。

那么，我们可以怎样增大 GNN 的感受野，使其具备更强大的能力呢？为此，我们需要更深或更宽的 GNN。

首先来看通过简单增加深度来扩展 GNN 的方法。可以看到，对于下图中的六种 GNN：GCN、GraphSAGE（进一步改进了池化方法）、ResGCN（使用了残差网络的思路）、JKNet（使用了 DenseNet 的思路）、IncepGCN（使用了 Inception-v3 的思路）、APPNP（借用了 PageRank 的思路），简单增加深度并不一定能提升准确度，甚至还可能出现相反的状况，比如 GCN、GraphSAGE 和 ResGCN 在深度增大时准确度反而显著下降。

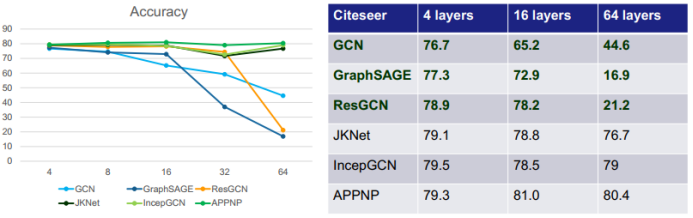
这不禁让人疑问：增加深度能提升表达能力的根本原因是什么？又是什么原因阻碍了 GNN 的深度扩展？

近期的研究找到了有碍 GNN 变得更深的三大根本原因：过平滑（over-smoothing）、过拟合（overfitting）和训练动态变化（training dynamics）。其中后两者也是常见的深度学习问题，而过平滑则是图深度学习方面特有的问题。