小波变换和motion信号处理：第二篇

说到这里，可能你对scaling function以及多解析度分析已经比较理解了。但是，我们还没有涉及到它们在小波变换中的具体应用，也就是还没有回答刚才那个问题：凭空插了一个scaling function到小波basis组合中干嘛。也就是说，我们希望理解scaling function是怎么和小波函数结合的呢，多解析度能给小波变换带来什么样的好处呢。这其实就是是小波变换中的核心知识。理解了这个，后面的小波变换就是纯数学计算了。

好，我们已经知道，对于子空间V0，basis是scaling function：

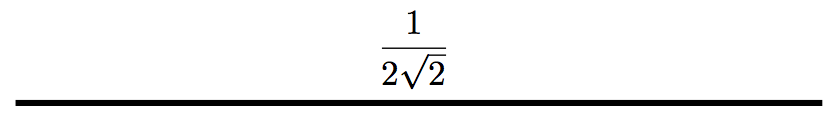
对应的小波函数是：

然后子空间V1的basis集合是这俩哥们：

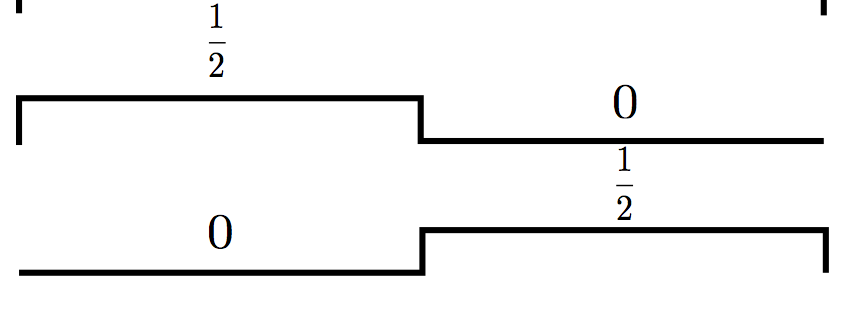
看出什么规律了么?多看几次这三个图，你会惊讶地发现，在V0中的scaling function和wavelet function的组合，其实就是V1中的basis!继续这样推导，V1本来的的basis是：

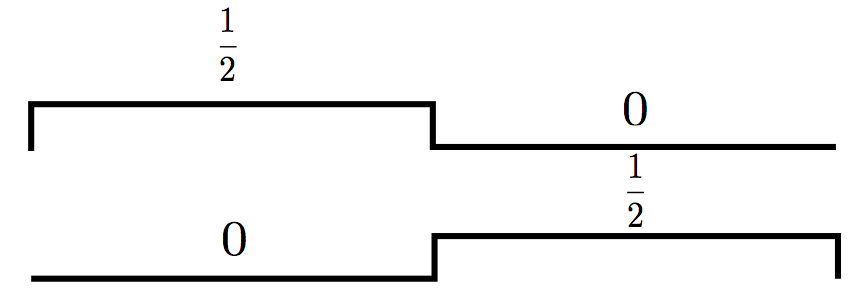
然后V1中对应的wavelet function是

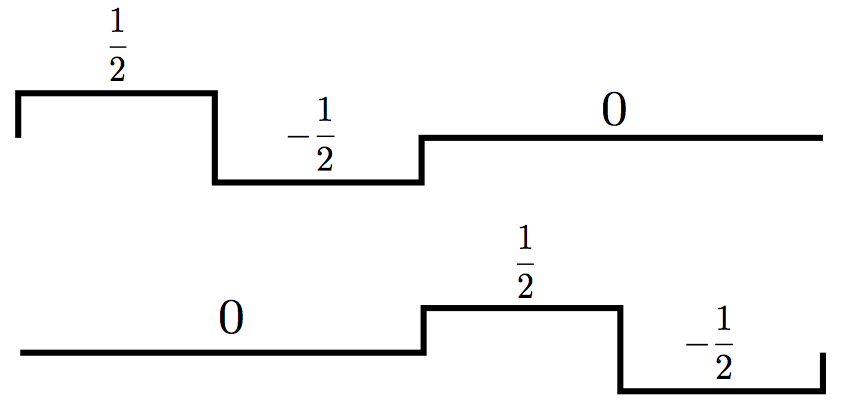
他们的组合，本质上也就是V2的basis(参考图2)。你继续推导下去，会得到同样的结论：在scale j的wavelet function，可以被用来将Vj的basis扩展到V(j+1)中去!这是一个非常非常关键的性质，因为这代表着，对任何一个子空间Vj，我们现在有两种方法去得到它的orthonormal basis：

1. 一种就是它本来的basis

，对任意k。

2. 第二种就是它上一个子空间的basis

，对任意k，以及上一级子空间的wavelet function

，对任意k。

第二种选择能给我们带来额外的好处，那就是我们可以循环不断地用上一级子空间的scaling function以及wavelet function的组合来作为当前子空间的基。换句话说，如果针对V3这个子空间，它实际上就有四种不同的，但是等价的orthonormal basis：

1. 本级(V3)的scaling function basis set

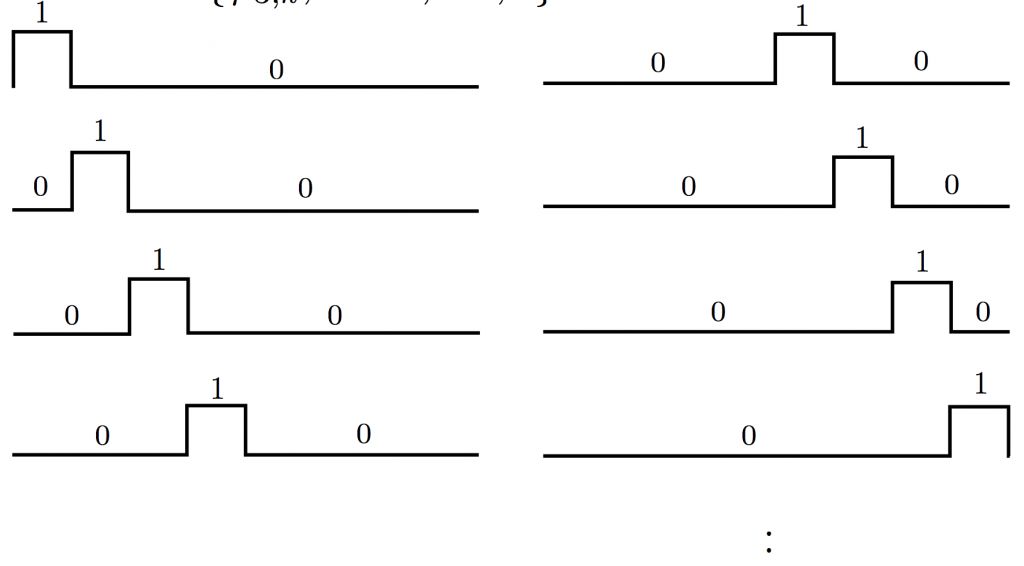
2. 上一级(V2)的scaling function + wavelet function;

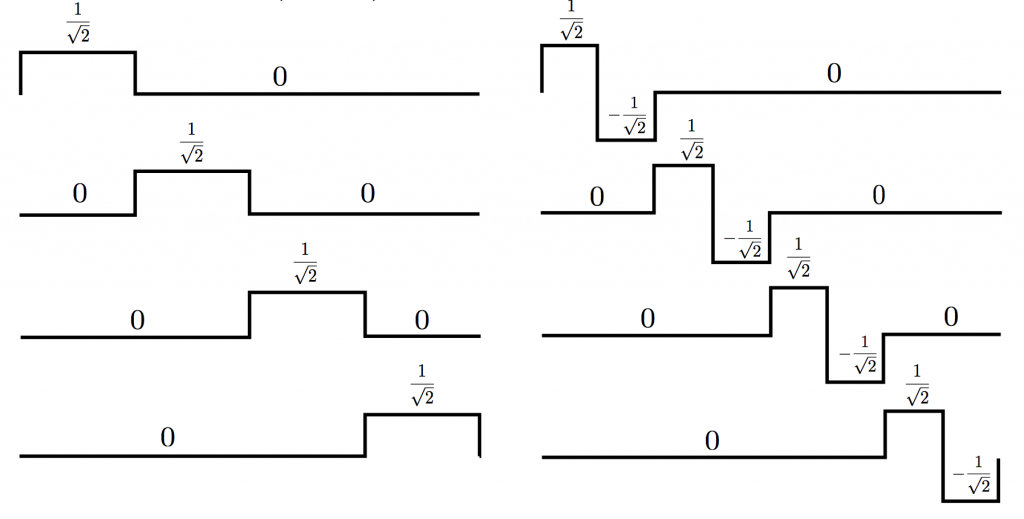
3 . 上上一级(V1)的scaling function + 上上一级(V1)的wavelet function + 上一级(V2)的wavelet function;

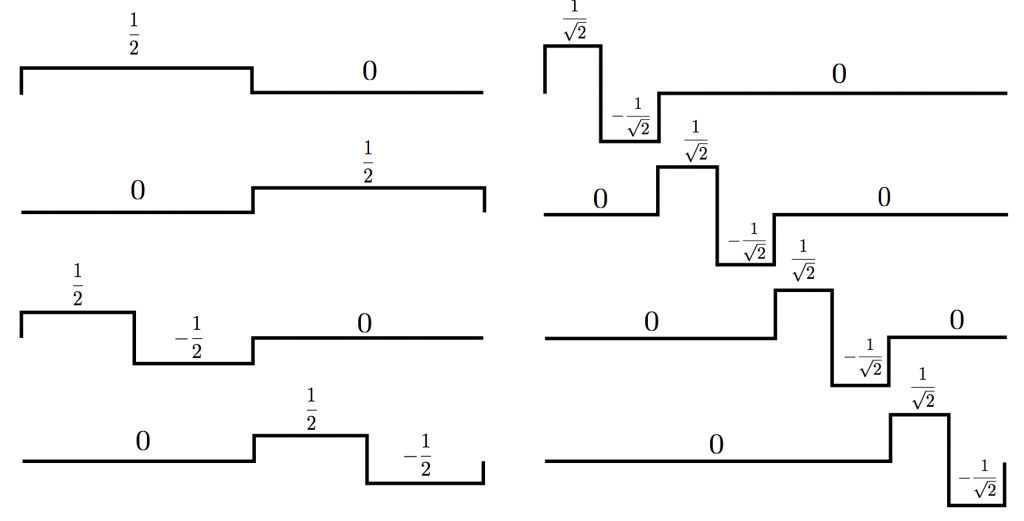
4. 上上上一级(V0)的scaling function + 上上上一级(V0)的wavelet function + 上上一级(V1)的wavelet function + 上一级(V2)的wavelet function

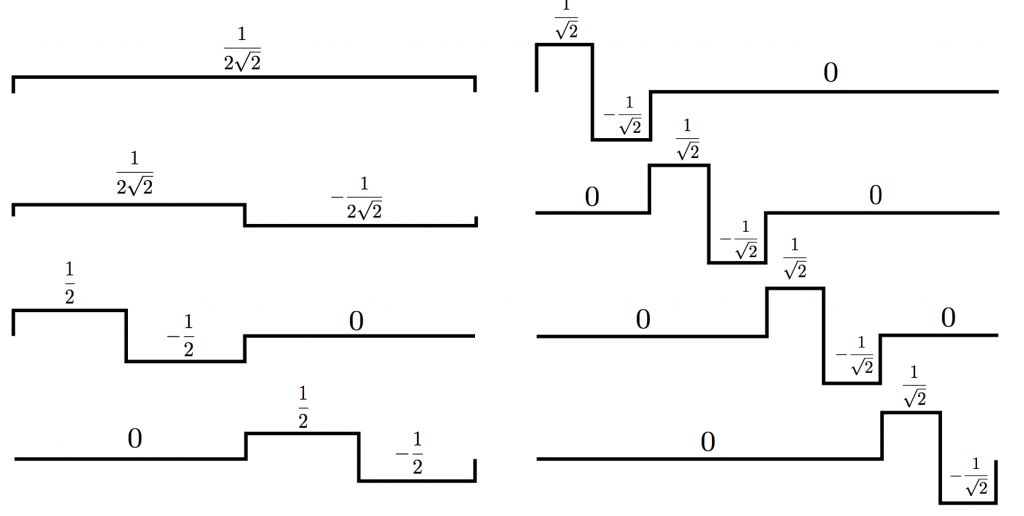
好，看看最后一种选取方式，有没有感到眼熟?对了，它就是我们之前提到的“针对此信号space的哈尔小波basis组合”，参见图1。现在我们知道了，这个scaling function不是凭空插进去的，而是通过不断的嵌套迭代出来的：)

那为什么我们最后选定的是这种选取方式呢?实际上，刚才介绍的这个性质已经告诉我们，对于任何的scale j0，我们都可以给我们的signal space找到一组orthonormal basis，这个basis是通过组合scale j0上的scaling function以及所有在scale j，j>j0上的wavelets得到的。这样，基于这个orthonormal basis，所有信号空间中的信号都可以写成组成这个basis的functions的线性组合：

对应的系数的计算和平常一样：

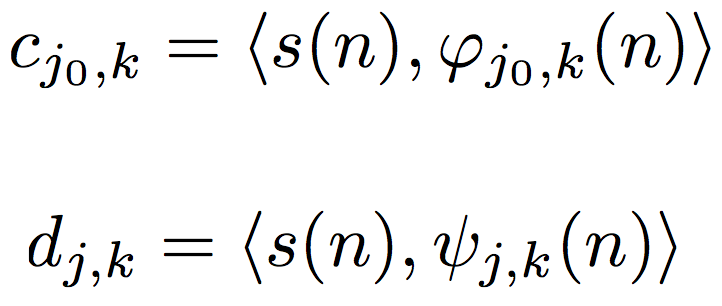
这，就是最终的，也是最核心的，小波变换形式。不管是信号压缩，滤波，还是别的方式处理，只要是用小波变换，都逃不出这个基础流程：

1. 选取合适的wavelet function和scaling function，从已有的信号中，反算出系数c和d。

2. 对系数做对应处理

3. 从处理后的系数中重新构建信号。

这里的系数处理是区别你的应用的重点。比如图像或者视频压缩，就希望选取能将能量聚集到很小一部分系数中的小波，然后抛弃那些能量很小的小波系数，只保留少数的这些大头系数，再反变换回去。这样的话，图像信号的能量并没有怎么丢失，图像体积却大大减小了。

还有一个没有解释的问题是，为什么要强调尺度函数和小波函数组成一个orthonormal basis呢?计算方便是一方面，还有一个原因是，如果他们满足这个性质，就满足瑞利能量定理，也就是说，信号的能量，可以完全用每个频域里面的展开部分的能量，也就是他们的展开系数表示：

到这里，我们对小波变换的形式就讲完了。虽然是用的最简单的哈尔小波为例子，但举一反三即可。我们着重介绍了多解析度分析以及它给小波变换带来的杀手锏：时域频域同时定位。结束之前，再多说几句小波变换的意义。我们拿刚才例子中V3子空间的第二种可选择的orthonormal basis作为例子：

左边这四个basis组成元素，也就是scaling functions，的系数，表征的是信号的local平均(想想它们和信号的内积形式)，而右边的这四个basis组成元素，也就是wavelet functions，的系数则表征了在local平均中丢失的信号细节。得益于此，多解析度分析能够对信号在越来越宽的区域上取平均，等同于做低通滤波，而且，它还能保留因为平均而损失的信号细节，等同于做高通滤波!这样，我们终于可以解释了wavelet function和scaling function背后的物理意义了：wavelet function等同于对信号做高通滤波保留变化细节，而scaling function等同于对信号做低通滤波保留平滑的shape!

对小波变换的基础知识，我们就讲到这里。需要注意的是，这只是小波变换最基本最基本的知识，但也是最核心的知识。掌握了这些，代表你对小波变换的物理意义有了一定的了解。但对于小波变换本身的讲解，一本书都不一定能将讲透，还有很多的基础知识我都没有讲，比如如何构建自己的scaling function，选取合适的系数集h[k]，并由此构建自己的wavelet functions。所以，如果有深入下去研究的同学，好好买一本书来看吧。而只是希望用小波变换来服务自己的应用的同学，个人觉得这些知识已经足够让你用来起步了。