利用1dB压缩点表征射频系统非线性

增益压缩导致电力系统从线性运行过渡到非线性运行。了解如何使用1 dB压缩点来定义线性操作的限制。

多种机制导致电子系统的非线性。例如，有源器件的跨导受到信号幅度的影响。这些器件内的寄生电容和电阻也与幅度有关，这会影响电路的性能。此外，即使短暂地超过电路的正常信号摆动，也会导致信号波谷或波峰的削波，给系统引入大量的非线性。

在高功率水平下，所有实际组件都表现出非线性。在射频电路中，这可能会导致损耗增加、信号失真，并可能对其他无线信道造成干扰。非线性可以用几种方式来表征，每种方式都为电路在不同条件下如何偏离线性行为提供了独特的视角。

在这篇文章中，我们将深入研究射频电路非线性的两种形式：谐波失真和增益压缩。我们还将探讨1 dB压缩点，这是表征增益压缩的有用指标。

1dB压缩点是什么？

如图1所示，1dB压缩点定义为输出功率比理想线性特性低1dB的功率电平。我们使用此规范来量化RF电路线性操作的上限。

1dB压缩点用作量化电路线性度的度量。

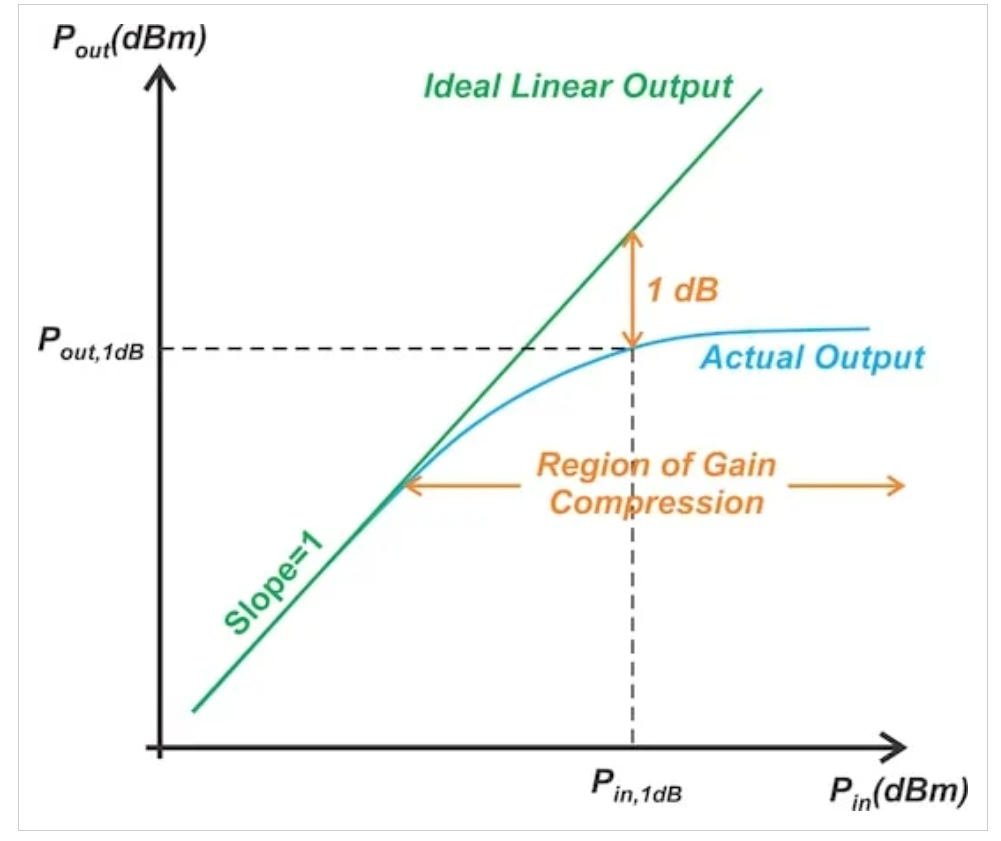
图1 1dB压缩点用作量化电路线性度的度量

1dB压缩点可以用输入或输出功率表示：

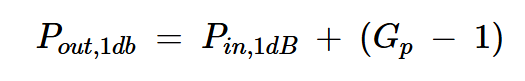
方程式1

其中：

Gp是放大器的理想线性增益，单位为分贝

Pin，1dB是发生压缩的输入功率

Pout，1dB是发生压缩的输出功率。

对于放大器，1 dB压缩点通常指定为发生压缩的输出功率。对于混音器，通常用与压缩点对应的输入功率来表示。RF接收器的输入压缩点通常在-20至-25 dBm的范围内。

现在我们知道1dB压缩点是什么了，让我们退一步，更广泛地考虑非线性系统的行为。本次讨论将为我们理解谐波失真和增益压缩奠定基础。稍后我们将回到1dB压缩点。

无记忆非线性系统建模

考虑一个具有输入x（t）和输出y（t）的设备或系统，如图2所示。

通用设备或网络。

图2 通用设备或网络

如果网络的传递特性为：

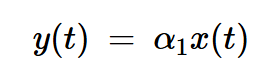
方程式2

其中⍺1是一个与时间无关的常数。如果不满足上述条件，则电路是非线性的。无记忆非线性系统的输入输出特性可以用多项式表达式近似：

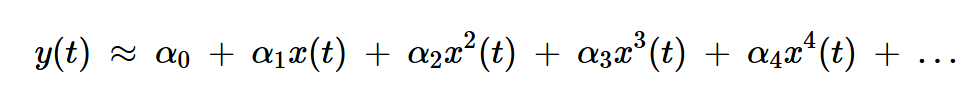
方程式3

我们通常在多项式表达式中保留高达三阶的项，导致：

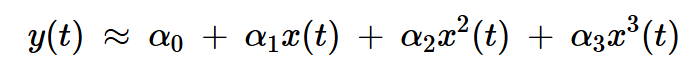
方程式4

请注意，在上述方程中，任何给定时间（t）的输出瞬时值仅由同一时刻的输入值决定。此条件定义了一个无记忆特性。如果时间t的输出受到先前输入值的影响，则该特性表现出记忆效应。

在有记忆的系统中，时滞输入或其导数和积分可能出现在输出方程中。例如，输出信号可以是以下列方式依赖于x（t）的函数：

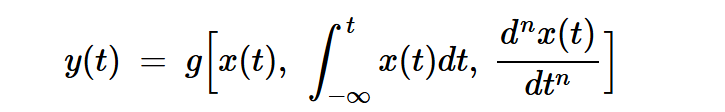
方程式5

谐波失真

多项式近似的非线性特性可以针对单音或双音输入进行检查。让我们看看如果我们将以下单音输入应用于方程4的非线性特性会发生什么：

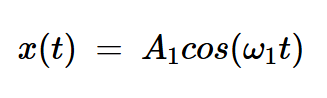
方程式6

我们获得：

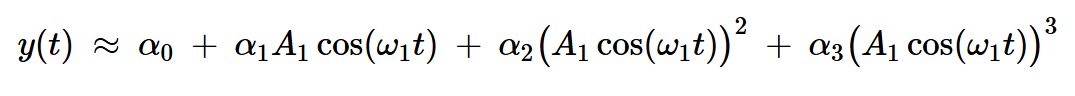
方程式7

二阶项产生的输出信号为：

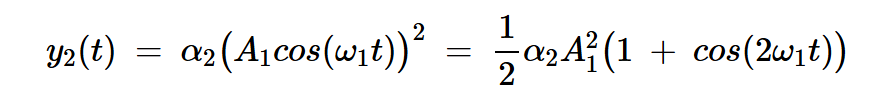
方程式8

二阶非线性在直流和二次谐波（2⍵1）处产生频率分量。

另一方面，三阶项产生：

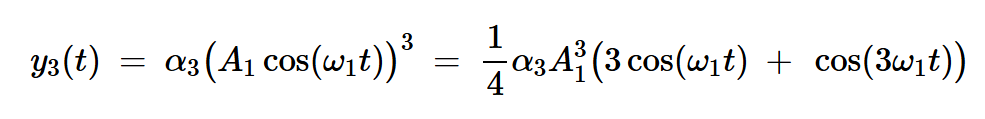
方程式9

三阶项产生基频和三次谐波（3⍵1）的频率分量。

结合方程7、8和9，三阶传递函数的总输出信号为：

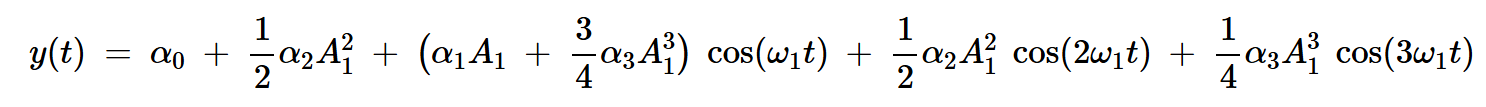
方程式10

当单音输入为⍵1时，方程的高阶项会在输入的所有谐波处产生频率分量。这种现象被称为谐波失真。

不同谐波下的输出功率

让我们假设上述讨论中的x（t）和y（t）是电压量。根据方程式10，基波电压分量的振幅为：

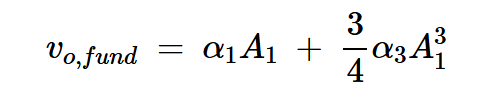
方程式11

⍵1处的总输出信号包括两个不同的项：线性项和三阶项。对于低水平的输入功率，线性项占主导地位。我们暂时忽略三阶项。

电阻归一化为1，基频下的输出功率为：

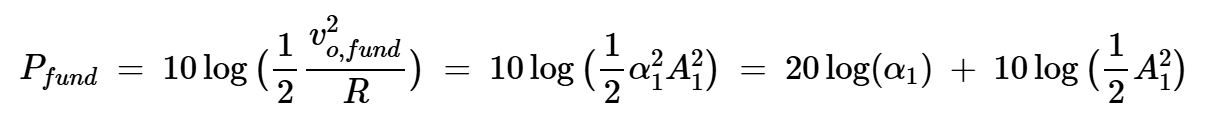
方程式12

上述方程中的最后一项是输入信号的功率：

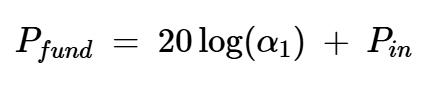
方程式13

这意味着，对于低输入功率值，输入功率每增加1dB，基本输出功率就会增加1dB。

二次和三次谐波分量呢？根据方程式10，二次谐波的输出功率为：

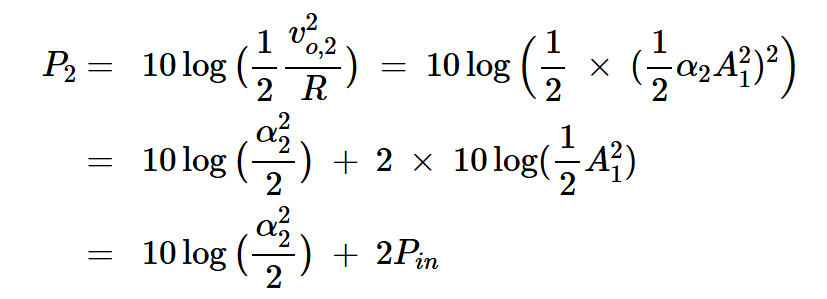
方程式14

因此，输入功率每增加1dB，二次谐波的输出功率就会增加2dB。同样，可以证明，对于三次谐波，输出功率与输入功率曲线的斜率为3:1。一般来说，当功率以分贝表示时，n次谐波的功率水平呈现出n:1的斜率。如图3所示。

不同谐波下的输出功率与输入功率。

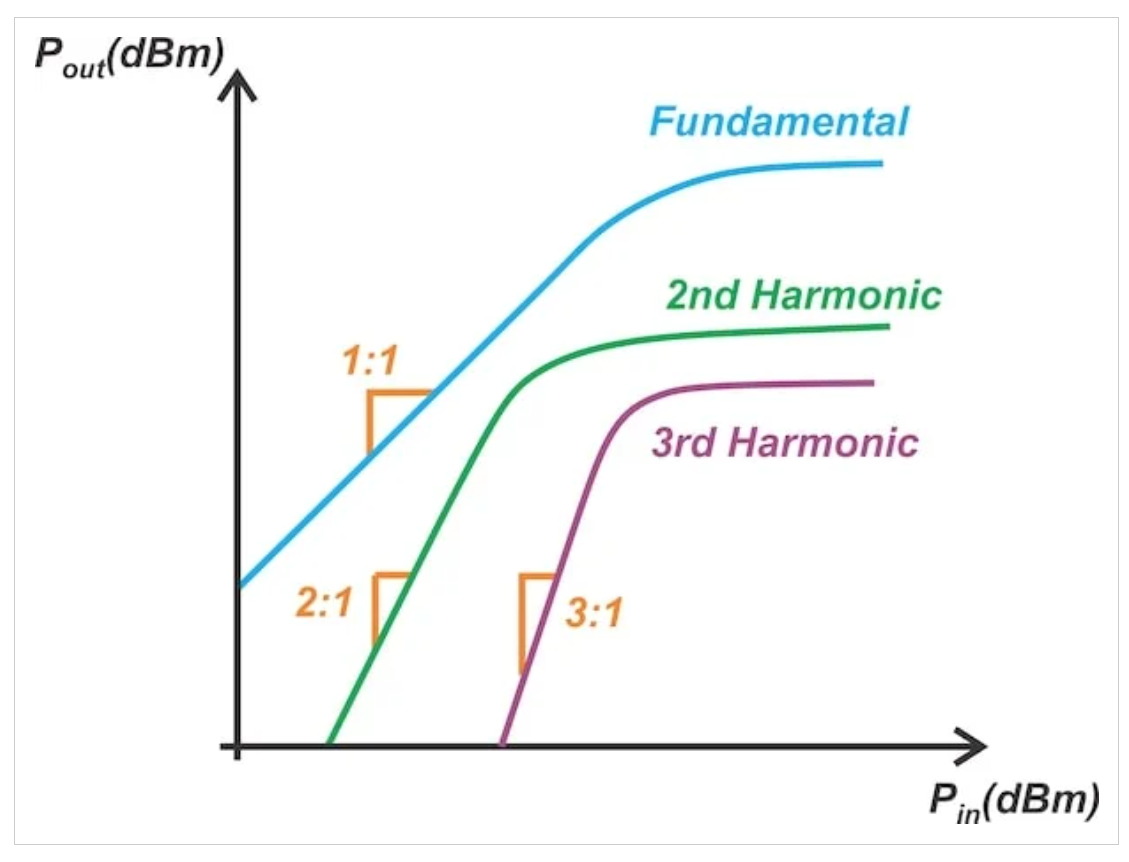
图3 不同谐波下的输出功率与输入功率

在弱非线性区域，输入功率每增加1dB，基频的功率就增加1dB。二次谐波和三次谐波分别上升2 dB和3 dB。

对于在弱非线性区域之外运行的实际电路，谐波频率中的功率可能不会相对于输入功率单调增加。这是由于我们的三次多项式表达式中忽略了高阶非线性项的影响。

增益压缩

在较高的输入功率下，输出开始饱和。这意味着输出功率不再随输入功率线性增加。一个原因是电源电压限制了电路的最大输出电压。

图3显示，放大器在基频下的增益取决于输入功率，并且随着输入功率的增加而下降。为了更好地理解这一点，让我们使用方程10来确定基频处的增益：

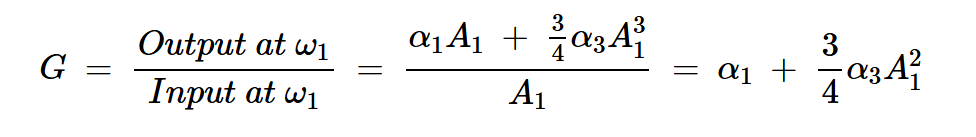
方程式15

在低输入功率下，⍺1项占主导地位，使增益等于放大器的小信号增益。然而，随着输入信号幅度的增加，上述方程中的第二项迅速增长。

对于大多数实际电路，⍺1和9082》3具有相反的符号。因此，在较高功率水平下增益会降低。这种现象被称为增益压缩。

确定1 dB压缩点

使用1dB压缩点作为度量，我们可以根据多项式表达式的系数确定压缩发生的信号幅度。应用本文开头给出的定义，方程15给出的放大器的实际增益比压缩点处的理想增益（⍺1）低1 dB。因此，我们有：

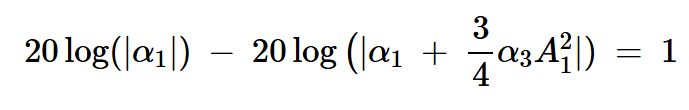
方程式16

其简化为：

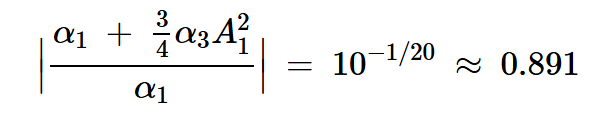
方程式17

最后，我们得到：

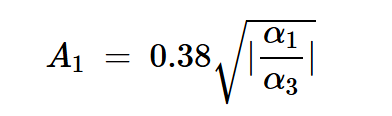
方程式18

这是发生1dB压缩的输入信号幅度。

关键要点

即使使用单音输入，非线性电路也会以输入频率的整数倍产生输出。这种现象被称为谐波失真。

此外，对于单音输入，非线性电路在基频处的总输出信号由线性项和三阶非线性项组成。在实际电路中，这会产生增益压缩。

为了量化电路线性区域的上限，我们使用1dB压缩点。这被定义为输出功率比理想线性特性低1dB的功率电平。