相量图与相量代数

相量图是一种用图形表示两个或多个交流量之间幅值和方向关系的工具。

相量图通过在坐标系中绘制图形，直观展示无源元件或整个电路中电压与电流之间的相位关系。通常，相量以参考相量为基准定义，参考相量始终沿x轴向右。

同频率的正弦波之间存在相位差，表示两个正弦波形之间的角度差异。常用“超前”“滞后”“同相”“异相”等术语描述正弦波形之间的关系。广义正弦表达式为：

A(t) = Am sin(ωt ± Φ) 该式以时域形式表示正弦波。

但通过数学公式表示时，有时难以直观理解两个（或多个）正弦波形之间的角度或相量差异。解决这一问题的方法之一是使用相量图在空间或相量域中图形化表示正弦波，这通过旋转矢量法实现。

旋转矢量（也称为“相位矢量”）是一条长度可变的线段，其长度代表交流量的幅值（“峰值”）和方向（“相位”），并在某一时刻“冻结”。矢量一端带有箭头，部分表示矢量的最大值（ Vm or Im），部分表示矢量的旋转末端。

通常假设矢量围绕固定零点（称为“原点”）旋转。带箭头的一端表示以角速度（ω）逆时针自由旋转的量。矢量的逆时针旋转被视为正旋转，顺时针旋转则为负旋转。

尽管“矢量”和“相量”均用于描述具有幅值和方向的旋转线段，但两者的主要区别在于：矢量的幅值是正弦波的“峰值”，而相量的复幅值是正弦波的“有效值”（RMS值），因为相量用于涉及电抗的交流电路。两者的相位角、方向和角速度相同。

交流量在任意时刻的相位可以通过相量图表示，因此相量图可视为“时间函数”的图形化表达。一个完整的正弦波可通过单个矢量以角速度ω=2πƒ逆时针旋转构建（ƒ为波形频率）。因此，相量是一个兼具“幅值”和“方向”的量。

此外，矢量遵循平行四边形加减法则，因此可以相加生成以角速度逆时针旋转的矢量和。相量则用数学上的直角坐标、极坐标或指数形式表示，例如（a+jb）。因此，相量符号定义了电压和电流的有效值（RMS值）。

绘制相量图时，通常假设正弦波的角速度为ω（弧度/秒）。观察以下相量图：

正弦波的相量图

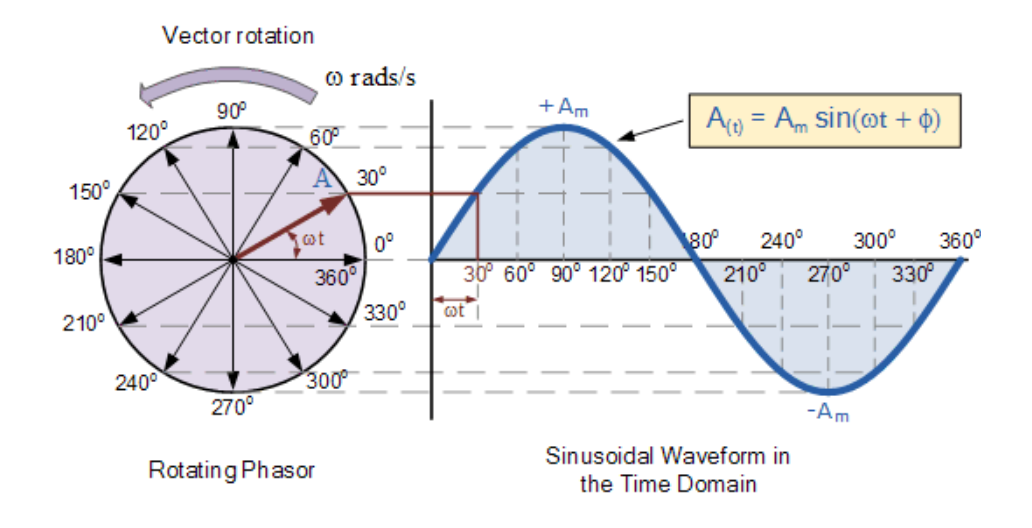
当单个矢量逆时针旋转时，其端点A将完成360°或2π弧度的完整旋转，代表一个完整周期。若将旋转端在不同时间点的位置投影到图中（如上所示），则从左端（零时刻）开始可绘制出正弦波形。水平轴的每个位置表示从零时刻（t=0）起经过的时间。当矢量水平时，其端点表示角度0°、180°和360°。

同理，矢量垂直时，其端点表示正峰值（+Am >，对应90°或π/2）和负峰值（ -Am，对应270°或3π/2）。波形的时间轴表示相量移动的角度（度或弧度）。因此，相量可视为旋转矢量在某一时刻（t）的“冻结”值，代表缩放后的电压或电流值。上例中，该时刻对应角度为30°。

分析交流波形时，有时需要知道相量在特定点的位置（尤其是比较同一轴上的两个不同波形时，例如电压和电流）。上例假设波形从t=0开始，具有相应的相位角（度或弧度）。

但如果第二个波形的起点位于零点的左侧或右侧，或需用相量符号表示两个波形的关系，则必须考虑波形的相位差Φ。观察以下相位差教程中的图示：

正弦波的相位差

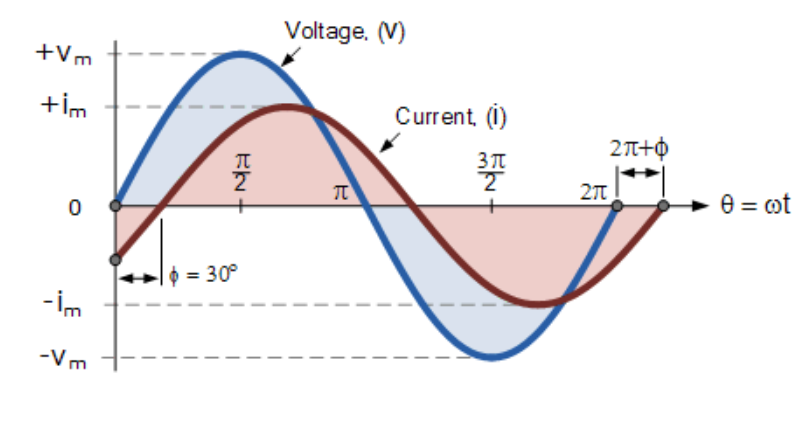
定义这两个正弦量的广义数学表达式为：

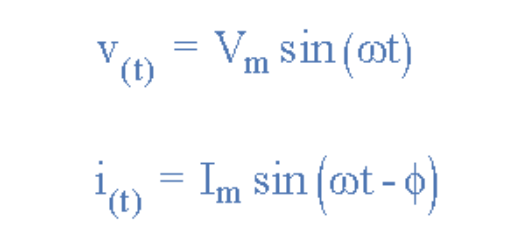
电流i滞后电压v的角度为Φ（上例中为30°）。因此，表示这两个正弦量的相量之间的差异为角度Φ，生成的相量图如下：

正弦波的相量图

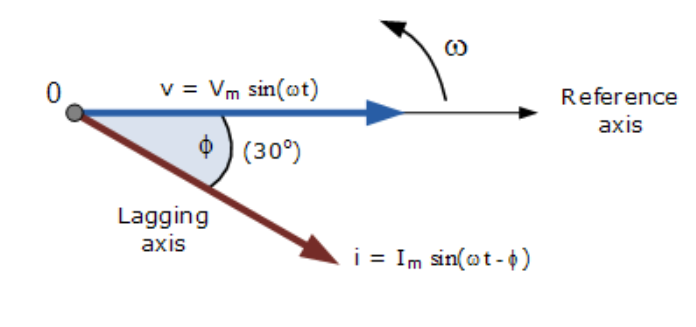
相量图对应时间零点（t=0）绘制在水平轴上。相量的长度与电压（V）和电流（I）在绘制时刻的瞬时值成比例。如前所述，电流相量滞后电压相量角度Φ，因为两个相量逆时针旋转，因此角度Φ也按逆时针方向测量。

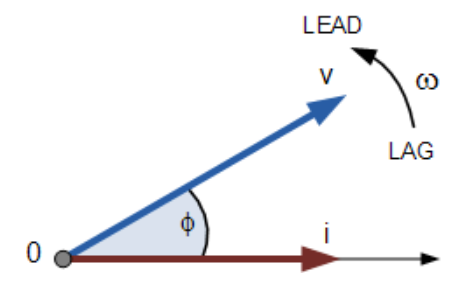
若将波形冻结在t=30°时刻，对应的相量图如右图所示。由于两个波形频率相同，电流相量仍滞后电压相量。但由于电流波形此时穿过水平零轴，可将电流相量作为新参考，并正确描述电压相量“超前”电流相量角度Φ。无论如何，一个相量被指定为参考相量，其他相量均相对于该参考相量超前或滞后。

相量图的加法

相量的一个重要用途是叠加同频率的正弦量。在研究正弦波时，有时需要将两个不同相的交流波形相加（例如交流串联电路中）。

若两个波形“同相”（无相位差），则可像直流值一样直接相加求矢量的代数和。例如，两个电压分别为50伏和25伏且同相时，它们相加结果为75伏（50+25）。

但如果它们不同相（方向或起点不同），则需考虑相位角，并通过相量图使用平行四边形法则求合成相量或矢量和。

假设两个交流电压V1（峰值20伏）和 V2（峰值30伏），且V1到V2 为60°。总电压VT可通过绘制相量图表示这两个矢量，并构造平行四边形（两边为V1和V2）求得，如下所示：

两个相量的加法

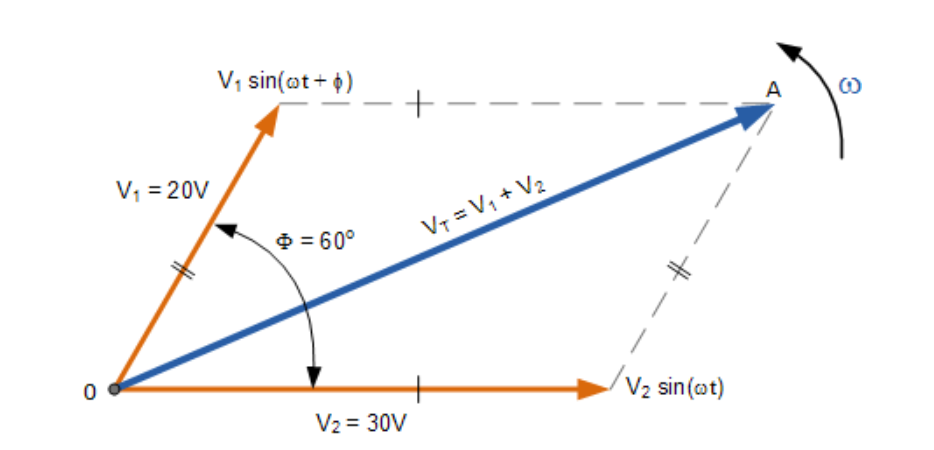
通过按比例绘制两个相量，其相量和V1+V2可通过测量对角线长度（称为“合成r矢量”）得到，即从零点到构造线0-A的交点。这种图形法的缺点是按比例绘制相量耗时，且若绘制不精确可能导致误差。

另一种确保结果准确的方法是解析法。数学上，可通过计算两个电压的“垂直”和“水平”分量，再求合成“r矢量”VT的分量来相加。这种利用余弦和正弦定理求合成值的方法称为直角坐标形式。

在直角坐标形式中，相量分为实部（x）和虚部（y），构成广义表达式Z=x±jy（下节将详细讨论）。由此得到表示正弦电压幅值和相位的数学表达式：

因此，使用广义表达式将两个矢量A和B相加的步骤如下：

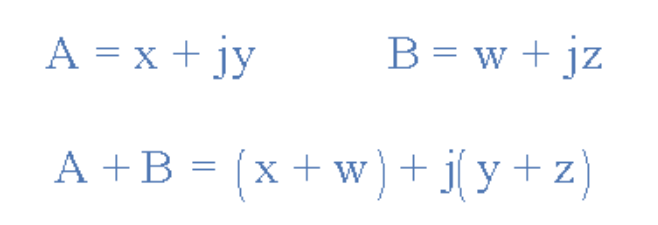
直角坐标形式的相量加法

假设电压V2（30伏）沿水平零轴方向，则其只有水平分量，无垂直分量：

-水平分量=30cos0°=30伏

-垂直分量=30sin0°=0伏

因此，V2的直角坐标表达式为：30+j0

电压V1（20伏）超前V260°，因此具有水平和垂直分量：

-水平分量=20cos60°=20×0.5=10伏

-垂直分量=20sin60°=20×0.866=17.32伏

因此，V1的直角坐标表达式为：10+j17.32

合成电压VT通过水平和垂直分量相加得到：

-水平分量=V1和V2实部之和=30+10=40伏

-垂直分量=V1和V2虚部之和=0+17.32=17.32伏

通过勾股定理计算90°三角形的斜边，得到VT的幅值：

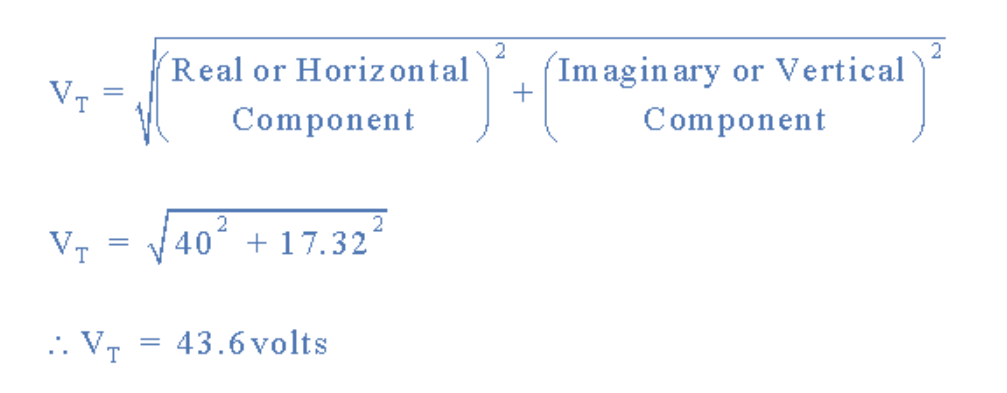
合成相量图如下：

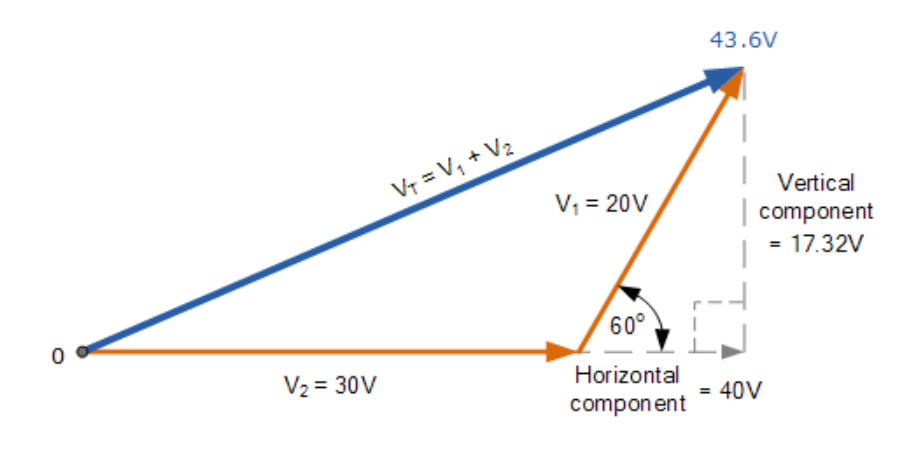
合成电压VT的确定

相量图的减法运算与前述直角坐标加法类似，但此时矢量差为电压V1和V2所构成平行四边形的另一条对角线，如下图所示：

两个相量的减法

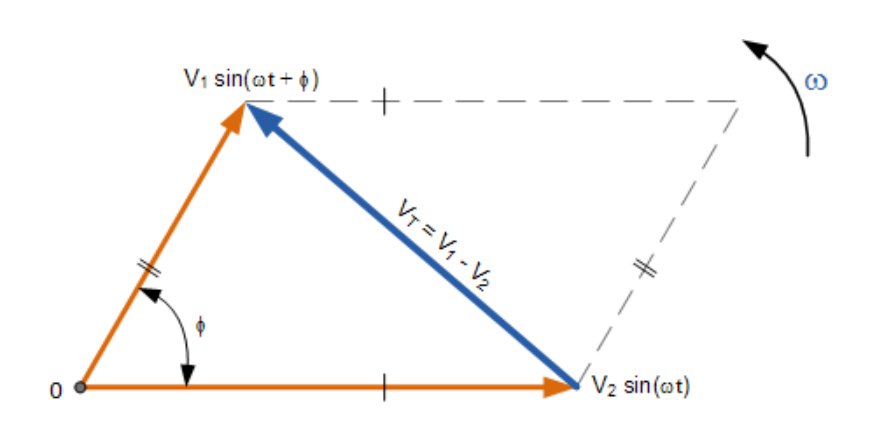
与加法不同，减法需对水平和垂直分量进行相减运算：

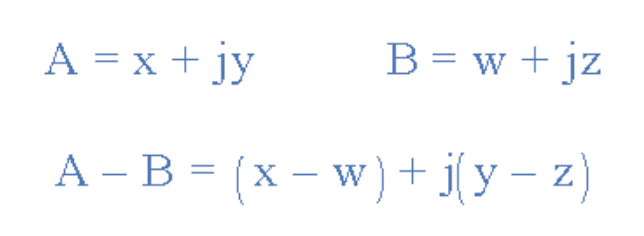
三相相量图

此前我们仅讨论了单相交流波形（单个多匝线圈在磁场中旋转）。若将三个匝数相同的线圈以120°电角度间隔安装在同一转子轴上，则可产生三相电压。

平衡三相电源由三个幅值、频率相同但相位互差120°的正弦电压组成。国际标准用红（R）、黄（Y）、蓝（B）三色标识相位，并以红色相位为参考相位。三相电源的标准相序为红→黄→蓝（R-Y-B）。

与单相相量类似，三相系统的相量也以角速度ω（弧度/秒）绕中心点逆时针旋转。下图展示星型（Y）或三角形（Δ）连接的三相平衡系统相量图：

三相星型连接相量图

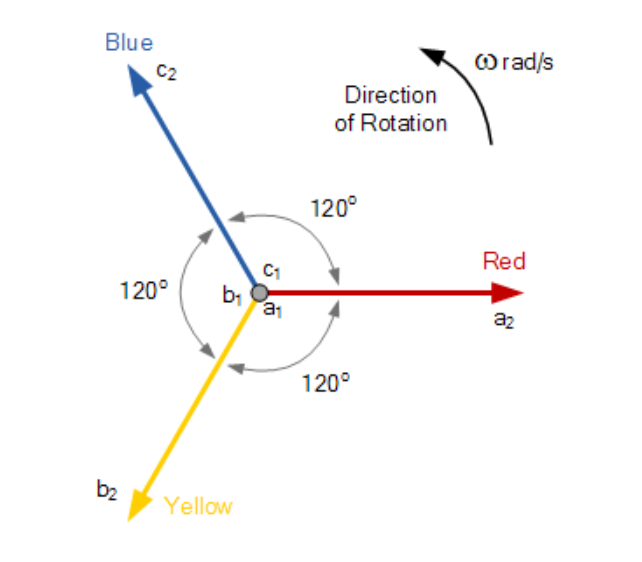
各相电压幅值相等，仅相位角不同。三个线圈绕组在a1、b1、c1点连接形成公共中性点。以红色相位为参考时，各相电压对中性点的表达式为：

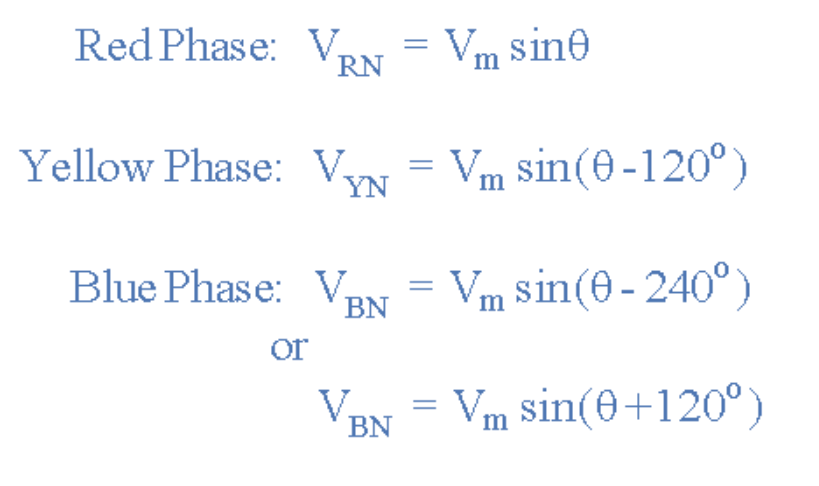
若以VRN为参考电压，则黄色相位电压滞后VRN120°，蓝色相位电压又滞后VYN120°。亦可表述为蓝色相位电压VBN超前VRN120°。

关于三相系统的关键特性：由于三个正弦电压的相位差恒为120°，它们构成“平衡”系统，因此其相量和恒为零：Va + Vb + Vc = 0

相量图要点总结

1.本质：相量图是旋转矢量在水平轴（瞬时值）上的投影，参考相量始终沿x轴正方向绘制。

2.适用范围：仅适用于正弦交流量。

3.多相量表示：可同时表示任意时刻两个及以上同频率正弦量（电压、电流等）。

4.绘制规则：

-参考相量置于水平轴，其他相量按相对位置绘制

-所有相量以逆时针方向旋转

-超前相量位于参考相量前方，滞后相量位于后方

5.幅值标准：相量长度通常代表有效值（RMS），而非峰值。

6.频率限制：不同频率的正弦波不可共用相量图（因旋转速度不同导致相位差动态变化）。

7.矢量运算：通过平行四边形法则可进行加减运算，合成单一矢量。

8.三相特性：平衡系统中各相量间隔120°。

在接下来的交流理论教程中，我们将探讨用复数（直角坐标式、极坐标式、指数式）表示正弦波形的方法。