AM信号平衡调制器介绍

了解平衡调制器在生成DSB-SC和传统AM信号时如何解决平方律调制器的缺点。

在本系列的前一篇文章中，我们学习了平方律调制器如何利用电子元件的二阶非线性来产生AM波。理论上，这种类型的调制器电路可以产生传统的AM和双边带抑制载波（DSB-SC）信号。然而，只有当非线性元件的输入-输出特性中的线性项和二阶项都不为零时，它才能产生DSB-SC信号。

在实践中，情况通常并非如此。此外，实际非线性元件的三次非线性会在平方律调制器的输出端产生不期望的信号分量。即使在生成传统AM信号时也是如此。

在本文中，我们将讨论如何通过在平衡配置中使用两个平方律设备来解决这些问题。这种被称为平衡调制器的装置可以产生DSB-SC和传统AM信号。然而，在我们深入探讨之前，让我们更详细地回顾一下平方律调制器及其局限性。

平方律调制器的局限性

图1中的平方律调制器通过将消息信号m（t）和载波c（t）之和发送通过非线性器件，然后通过适当调谐的带通滤波器，产生AM波。

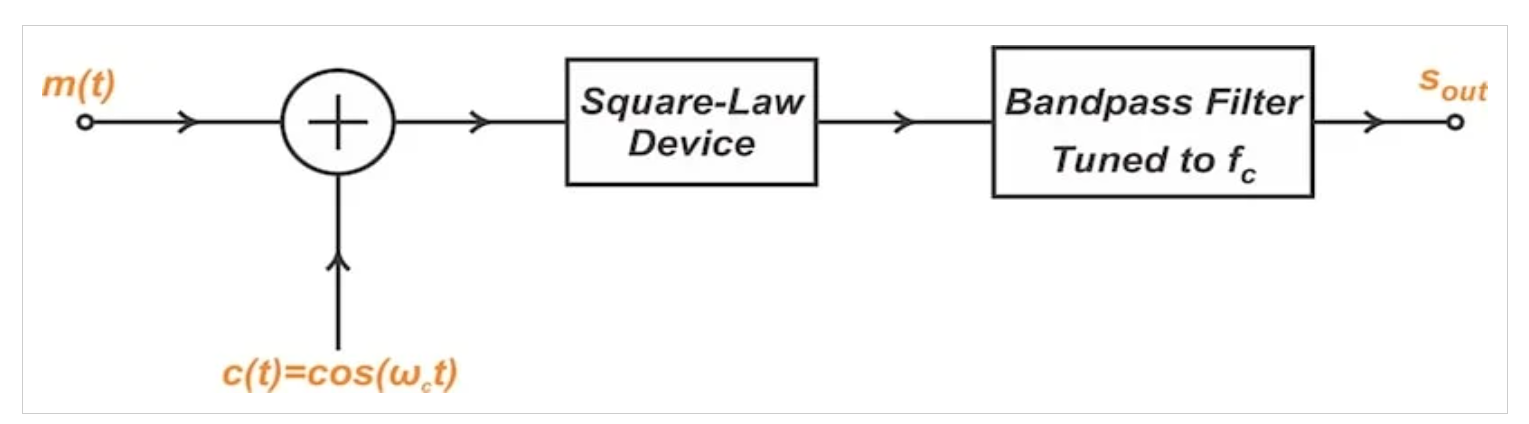
图1平方律调制器的方框图

在上一篇文章中，我们假设图1中平方律装置的输入输出特性由下式表示：

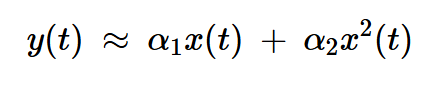
方程式1

在这种情况下，输出端的常规AM信号由下式给出：

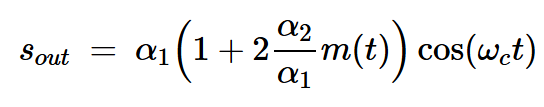
方程式2

其中调制指数为：

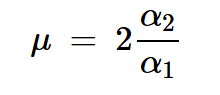
方程式3

除非方程1中的α1=0，否则平方律调制器无法产生DSB-SC信号。如前所述，这在实践中不会发生。

方程1的另一个局限性是它只包括α1和α2。同时，实际的非线性器件在其幂级数展开中通常包含超过二阶的非线性项。这些高阶项会在调制器的输出端产生不期望的分量。

为了理解这一点，假设非线性器件的输入输出特性可以表示为：

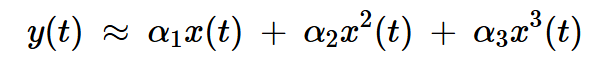
方程式4

方程式5显示了如果我们通过方程式4中的三次项（m（t）+cos（⍵ct）），输出端出现的分量：

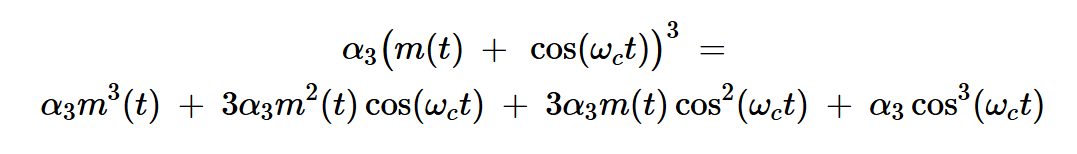
方程式5

我们可以将这个方程的结果分解如下：

第一项 ${\alpha }_3{m}^3\left(t\right)$生成以f=0为中心的光谱分量。

第二项3α3m3(t)cos(ωct)以f=fc为中心。

第三项3α3m3(t)cos2(ωct)产生直流分量以及二次谐波（2fc）周围的分量。

第四项α3cos3(ωct)产生基波（fc）和三次谐波（3fc）分量。

让我们使用方程6中的三角恒等式来仔细研究第四项。

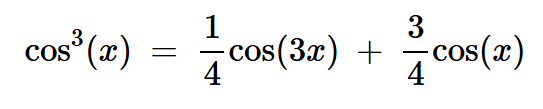
方程式6

由于非线性器件后面是调谐到fc的带通滤波器，因此该三次项在载波频率周围产生以下附加分量：

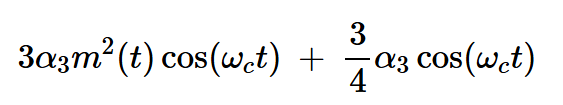
方程式7

方程式7的第一项将频率为fc的消息信号的平方与所需的AM波相加。由于该分量会干扰AM波，因此需要一个非线性器件，其高阶系数（n≥3时为⍺n）与9082》2相比可以忽略不计。否则，我们需要限制输入信号的幅度，以保持高阶非线性项相对较小。

使用平衡调制器是另一种选择。在下一节中，我们将介绍平衡调制器的基本原理，并解释它如何产生DSB-SC信号。我们将在本文后面回过头来讨论它如何处理上述不需要的信号分量。

利用平衡调制器产生DSB-SC信号

图2显示了平衡调制器的框图。

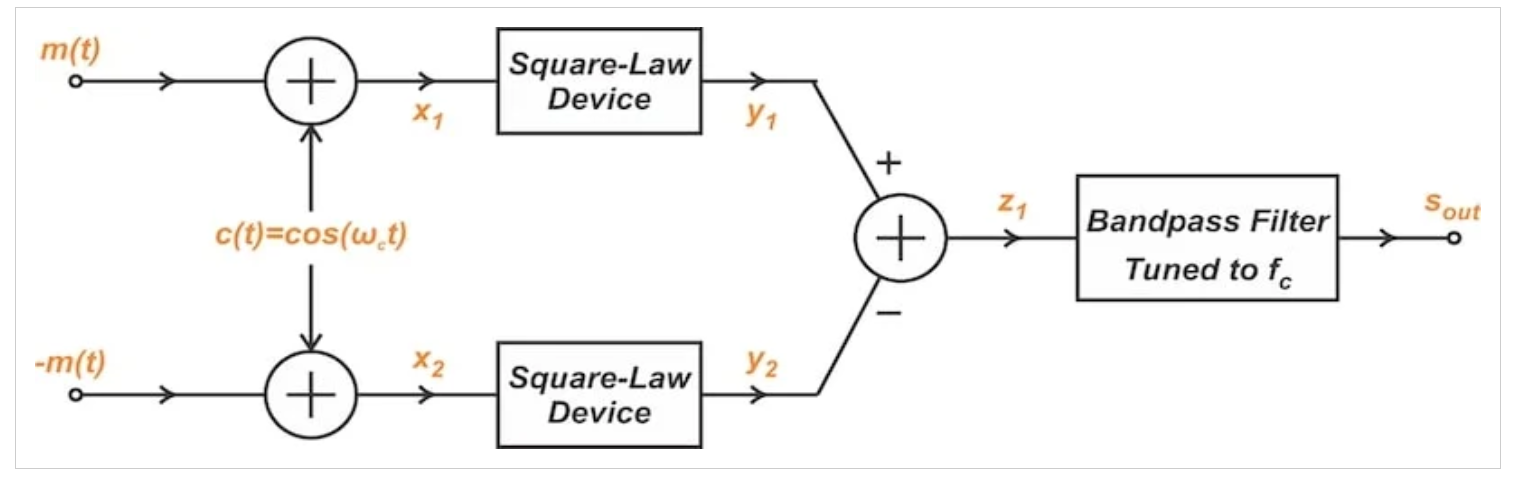
图2平衡调制器的方框图

如您所见，平衡调制器包含两个相同的平方律调制器——平衡调制器的两个信号路径各一个。一条路径接收消息信号m（t）；另一条路径被馈送消息信号的反转形式-m（t）。非线性器件的输出信号相互相减，然后将得到的信号通过带通滤波器。

为了了解平衡配置如何在⍺1≠0的情况下产生DSB-SC信号，让我们暂时抛开器件的三次非线性。因此，非线性元件的输入-输出特性可以用下式描述：

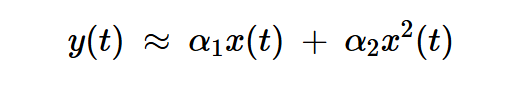
方程式8

图2左侧两个加法器输出端的信号为：

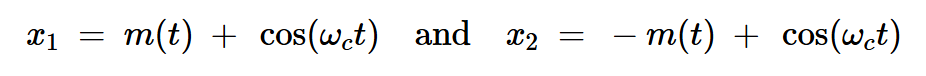
方程式9

结合方程式8和9，上部非线性装置输出端的信号为：

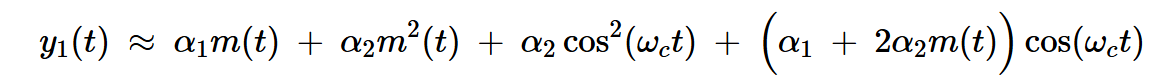
方程式10

在上述方程中用-m（t）替换m（t）会在较低非线性器件的输出端产生信号：

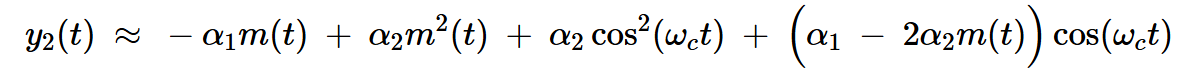
方程式11

从y1（t）中减去y2（t），我们得到信号z1（t）：

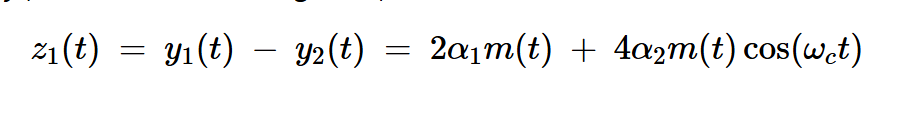
方程式12

在上述方程中，第一项是基带信号。第二项是以fc为中心的期望DSB-SC信号。带通滤波器调谐到fc，只允许AM信号通过输出，产生以下方程式：

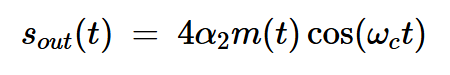
方程式13

这是一个DSB-SC信号，因此施加到输入端的载波不会出现在最后一个加法器的输出端。相反，该电路相对于输入c（t）=cos（⍵ct）起着平衡电桥的作用。电路的另一个输入m（t）出现在节点z1处（方程式12）。

因为它只相对于一个输入端是平衡的，所以我们将电路称为单个平衡调制器。在双平衡调制器中，两个输入都被抵消。输出端只有消息信号和载波的乘积可用。

高阶非线性项对平衡调制器的影响

接下来，让我们看看当非线性器件在其幂级数展开中包含三次项时会发生什么。三次项在节点y1处产生以下不期望的信号分量：

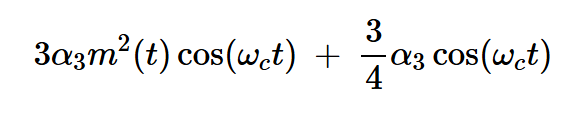
方程式14

为了找到由较低路径产生的不期望的信号分量，我们应该在上述方程中将m（t）替换为-m（t）。然而，很明显，反转消息信号不会影响不需要的术语。相反，由于不期望的项存在于节点y1和y2处，因此它们在减法时在输出处相互抵消。

请注意，平衡调制器中的两个非线性器件应表现出大致相同的特性。否则，它们将无法消除不需要的信号分量。

用平衡调制器产生传统AM信号

到目前为止，我们只讨论了DSB-SC信号的平衡调制器。但是传统AM呢？

方程式15再现了用于生成传统AM信号的基本方程式：

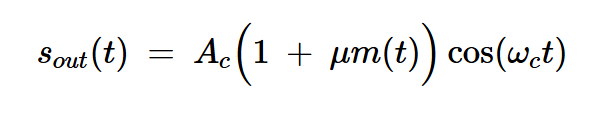
方程式15

为了使该方程适用于平衡调制器，我们注意到以下几点：

平衡调制器有效地充当了乘法器。

我们对平衡调制器的分析对输入消息信号没有限制。

鉴于上述情况，我们可以理想地将具有任意调制指数的1+μm（t）应用于平衡调制器，以产生传统的AM信号。如图3所示。

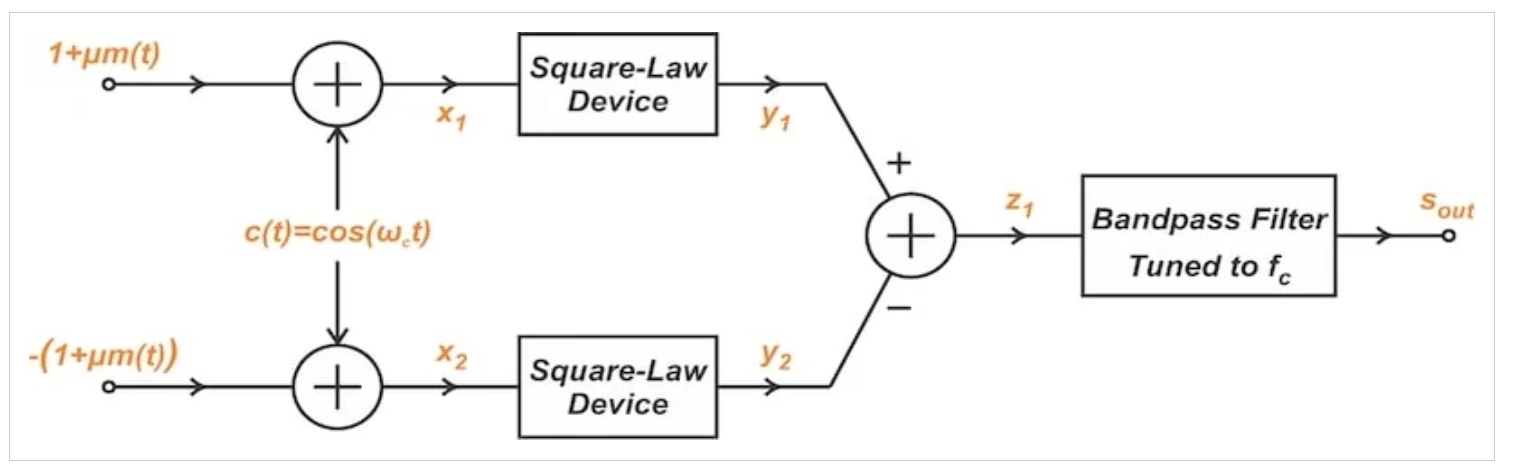
图3使用平衡调制器生成传统AM信号

用1+μm（t）代替方程13中的m（t，上述电路的输出为：

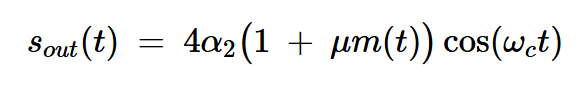
方程式16

其为常规AM波。

当使用平衡调制器创建传统AM信号时，重要的是要记住，对于特定范围的输入值，实际的非线性元件可能会表现出平方律特性。例如，只有当输入为正时，非线性分量的输出才可能与输入的平方成正比。

如果是这样的话，我们需要将非线性元件的输入限制在设备表现出预期平方律响应的范围内。这限制了使用图3中的技术时可以实现的调制指数。然而，我们可以根据需要增加调制指数，方法是将输入信号限制在允许的范围内，然后从调制器输出端的sout（t）中减去适当缩放的载波版本。

一种实用的平衡调制器电路

让我们通过简要检查一个示例电路实现来结束我们的讨论（图4）。

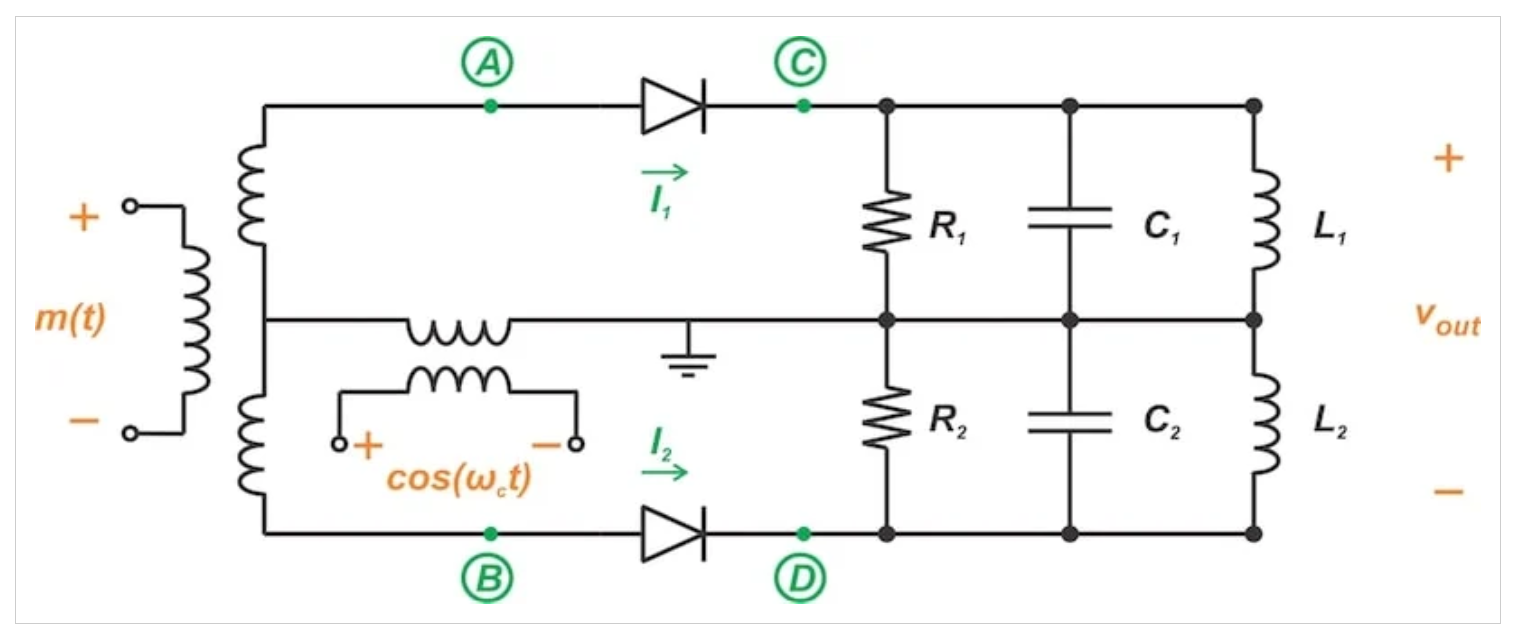
图4平衡调制器的示例电路实现

该电路使用变压器将载波与消息信号组合在一起。所需的带通滤波器采用LC谐振电路的形式，调谐到调制器输出端的载波频率。为了引入所需的非线性，使用了二极管。

图4中通过二极管的电流与二极管两端的电压呈非线性关系。为了理解这一点，让我们假设节点C处的电压远小于节点A处的电压。如果是这样的话，我们可以通过节点A（vA）处的电压来近似二极管两端的电压。然后，通过二极管（I1）的电流可以用功率级数来描述：

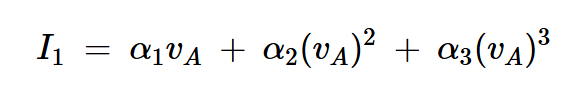
方程式17

这与我们之前在分析通用平衡调制器时使用的三阶表达式相同。

关键要点

我们可以在平衡配置中使用两个平方律器件来生成DSB-SC或传统AM信号。然而，在后一种情况下，非线性元件的输入范围限制会限制可实现的调制指数。尽管如此，平衡调制器仍然比平方律调制器具有重要优势——它消除了实际非线性元件产生的（潜在的重要）不期望的信号分量。