传输线元件阻抗匹配介绍

了解使用传输线元件的阻抗匹配技术。

在本系列的前一篇文章中，我们讨论了如何使用集总元件将一个阻抗转换为另一个所需值。集总匹配网络的应用频率通常限制在几千兆赫，因为在高频下，集总组件的寄生效应变得更加明显。还有另一种选择，即基于传输线的匹配网络，更适合高频应用。在本文中，我们将探讨这种阻抗匹配技术。

传输线输入反射系数

为了更好地理解基于传输线的阻抗匹配，重要的是要了解当我们沿着以给定负载阻抗ZL终止的传输线移动时，输入阻抗和反射系数是如何变化的。考虑图1中的下图。

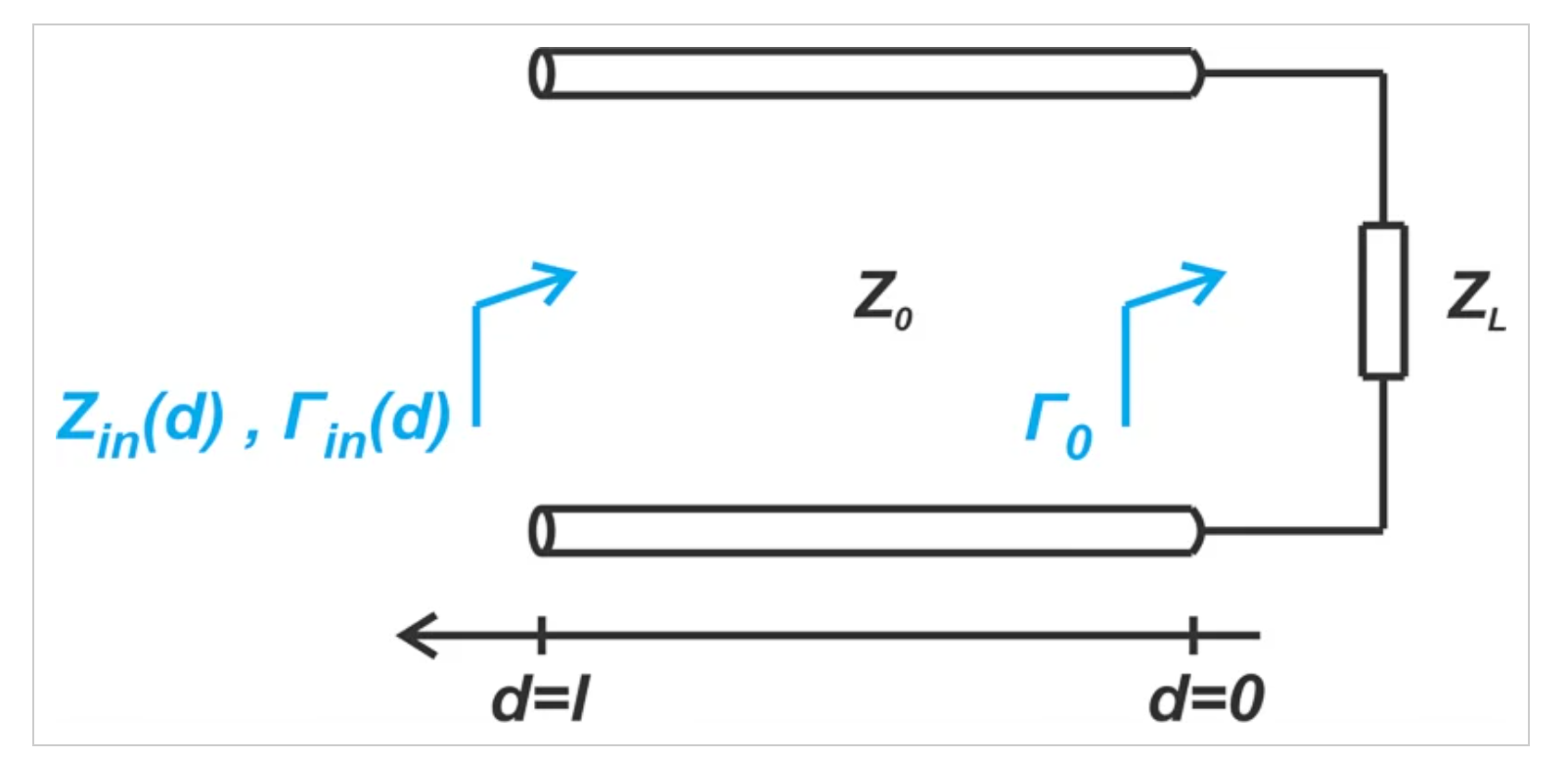
图1示出负载阻抗和反射系数的传输线的图

可以证明，（d）中距离负载d处的反射系数Γ由下式给出：

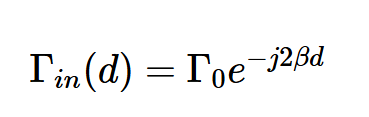
方程式1

解释：

β是相位常数

Γ0为荷载反射系数

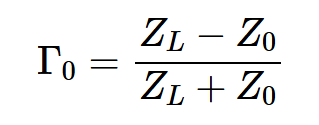
方程式2

方程1显示了反射系数如何沿线变化——（d）中Γ的大小是恒定的，等于Γ0的大小——然而，它的相位角随距离负载的距离（d）呈线性变化。

接下来，让我们来看一个例子。

示例1：找到输入阻抗和反射系数

求出端接在ZL=100+j50Ω负载阻抗的βd=71.585°的50Ω线路的输入阻抗和反射系数。

通过应用方程式2，我们首先找到负载端的反射系数：

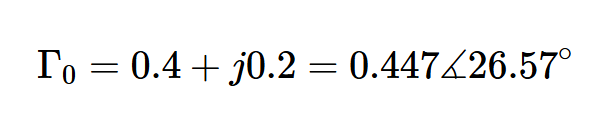
图2在史密斯圆图上定位Γ0（归一化阻抗为Z0=50Ω）。

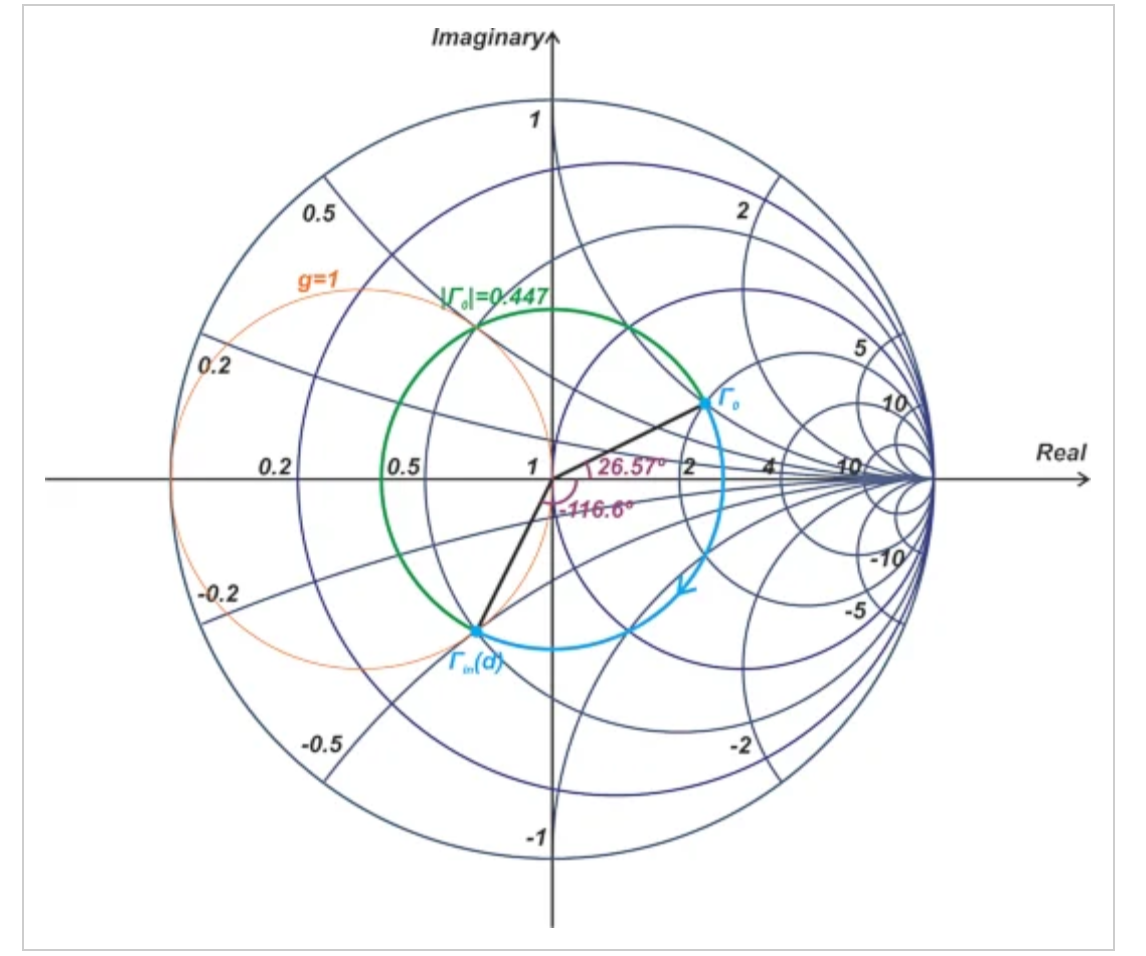
图2史密斯圆图显示Γ0和Z0=50Ω的归一化阻抗

在这个例子中，βd参数（称为线路的电气长度）为71.585°。根据方程1，（d）中Γ的相位角是Γ0减去2×71.585=143.17°的相位。因此，（d）中Γ的相位角为26.57°-143.17°=-116.6°。

图2显示了如何使用史密斯圆图从Γ0以图形方式获得（d）中的Γ；对于给定的Γ0，（d）中沿传输线Γ的反射系数位于半径为|Γ0|的圆上。一般来说，离开传输线上的终端会产生沿常数|Γ|圆的顺时针旋转。在史密斯圆图上，电长度为θ的线会导致2θ的旋转。

关于阻抗和传输线的两个重要观察

考虑一条电气长度为180°的线（对应于d=λ/2）。这样的线产生完整的360°旋转，并将我们带回我们开始的原始负载阻抗ZL。这意味着我们沿着传输线观察到的阻抗每半个波长重复一次。

图2还暗示了输电线路的一个重要特性；传输线可以将我们从一个恒定的电阻圈移动到另一个。在上面的例子中，一条71.585°的长线将我们从r=2的恒定电阻圆移动到r=0.5的圆。这意味着传输线可以充当阻抗匹配组件。我们很快就会回到这个例子，更详细地讨论基于传输线的阻抗匹配技术，但在深入探讨之前，让我们先了解史密斯圆图的波长尺度。

史密斯圆图波长标度

如上所述，传输线的输入阻抗可以通过史密斯圆图上的简单圆周运动来找到。我们也可以使用线的物理长度来表征线，而不是使用线的电长度，物理长度通常表示为波长的一部分。

这种等价性的控制方程是（βd=frac{2πd}{λ}）。例如，45°、90°、135°和180°的βd值可以分别由以下物理长度产生：

λ / 8

2λ / 8 = λ / 4

3λ / 8

4λ / 8 = λ / 2

这就是为什么史密斯圆图通常会沿图的周长提供波长标度，如图3所示。

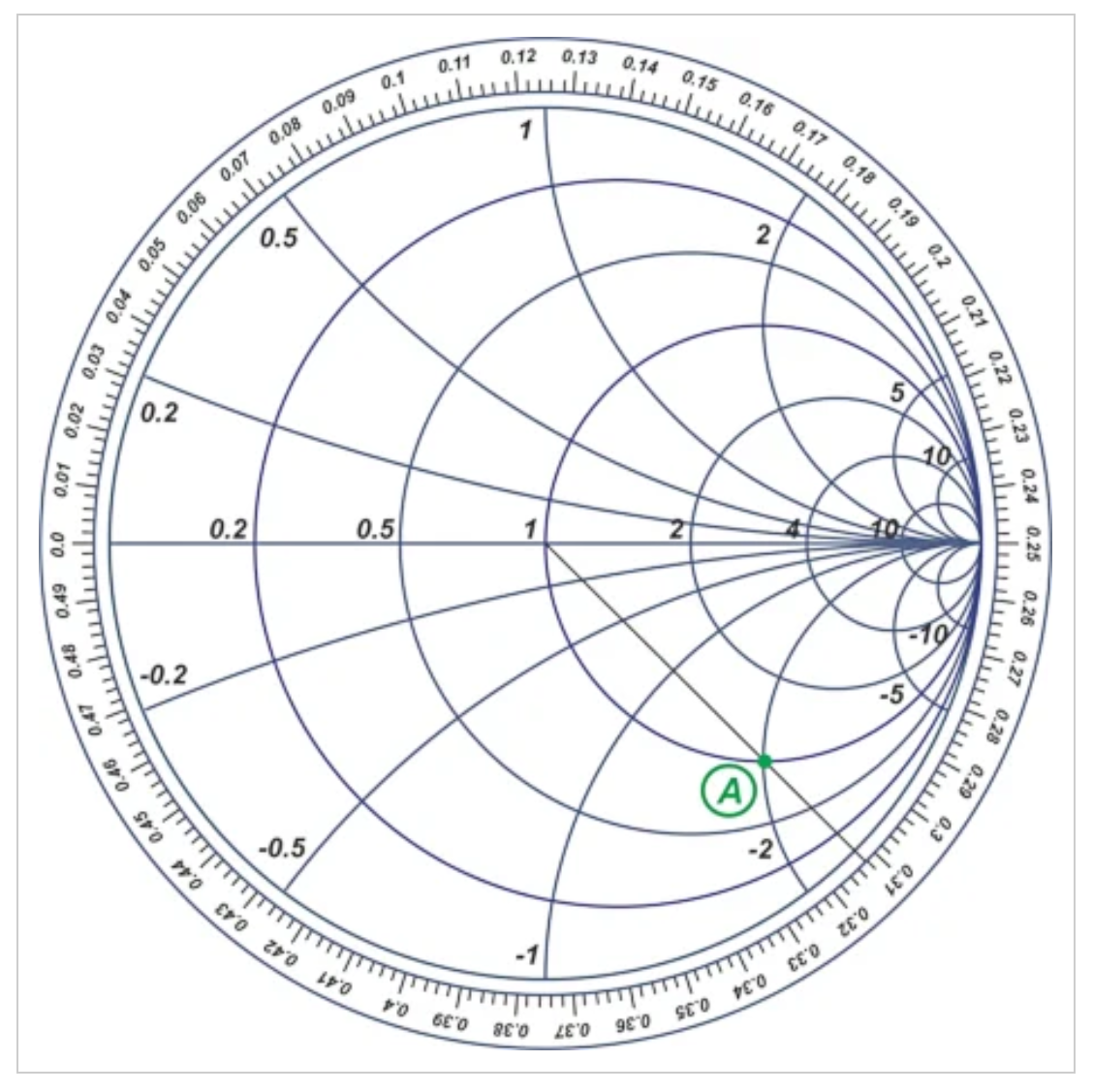
图3史密斯圆图示例，其周长周围有波长刻度

波长标度为史密斯圆图上的每个点指定了距离d。例如，上图中的点A对应的距离约为0.312λ。请注意，波长标度上显示的绝对值并不重要；我们主要使用这个尺度来计算传输线上两点之间的波长距离。

下面，我们将通过一个例子来阐明如何使用波长标度来解决传输线问题。在我们继续之前，请注意，由于电长度βd=180°（对应于d=λ/2）在史密斯圆图上产生360°的完整旋转，史密斯圆图的波长范围为0到0.5λ。

示例2：使用波长标度解决传输线问题

假设在距离负载阻抗ZLoad l1=0.051λ处，输入阻抗为Z1=50-j50Ω（下图4）。

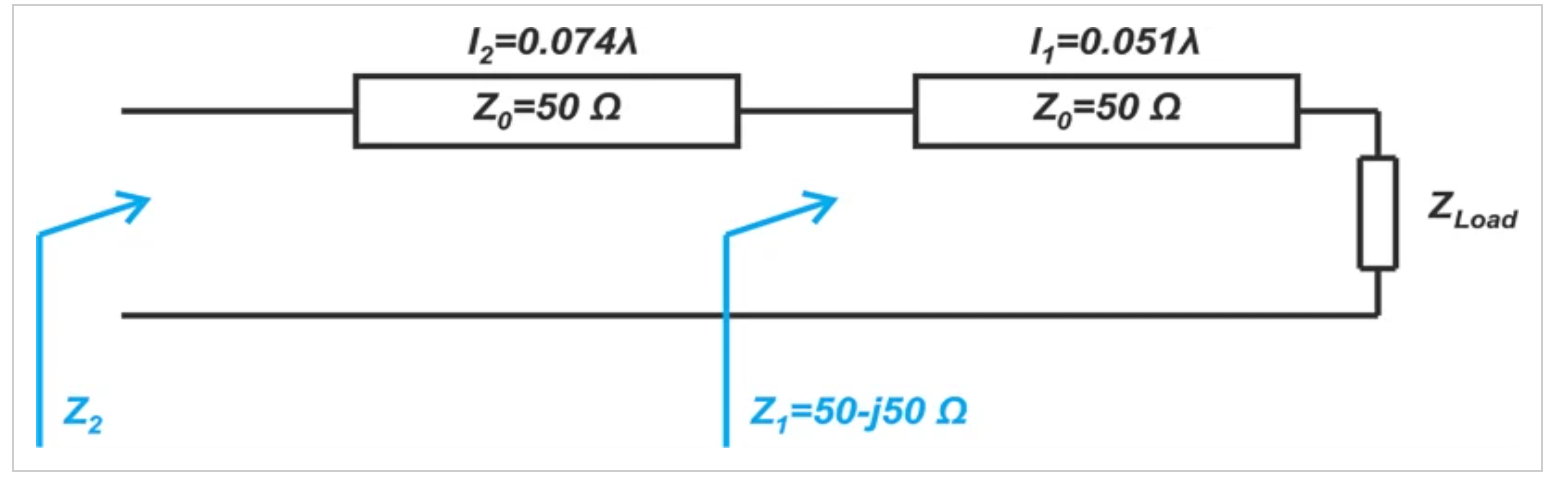
图4显示示例传输线的距离、负载和输入阻抗的图

在距离Z1 l2=0.074λ处找到ZLoad和输入阻抗Z2。假设两条线路的特性阻抗均为50Ω。

使用50Ω的归一化阻抗，Z1的归一化值为Z1=1-j，如下图所示（图5）。

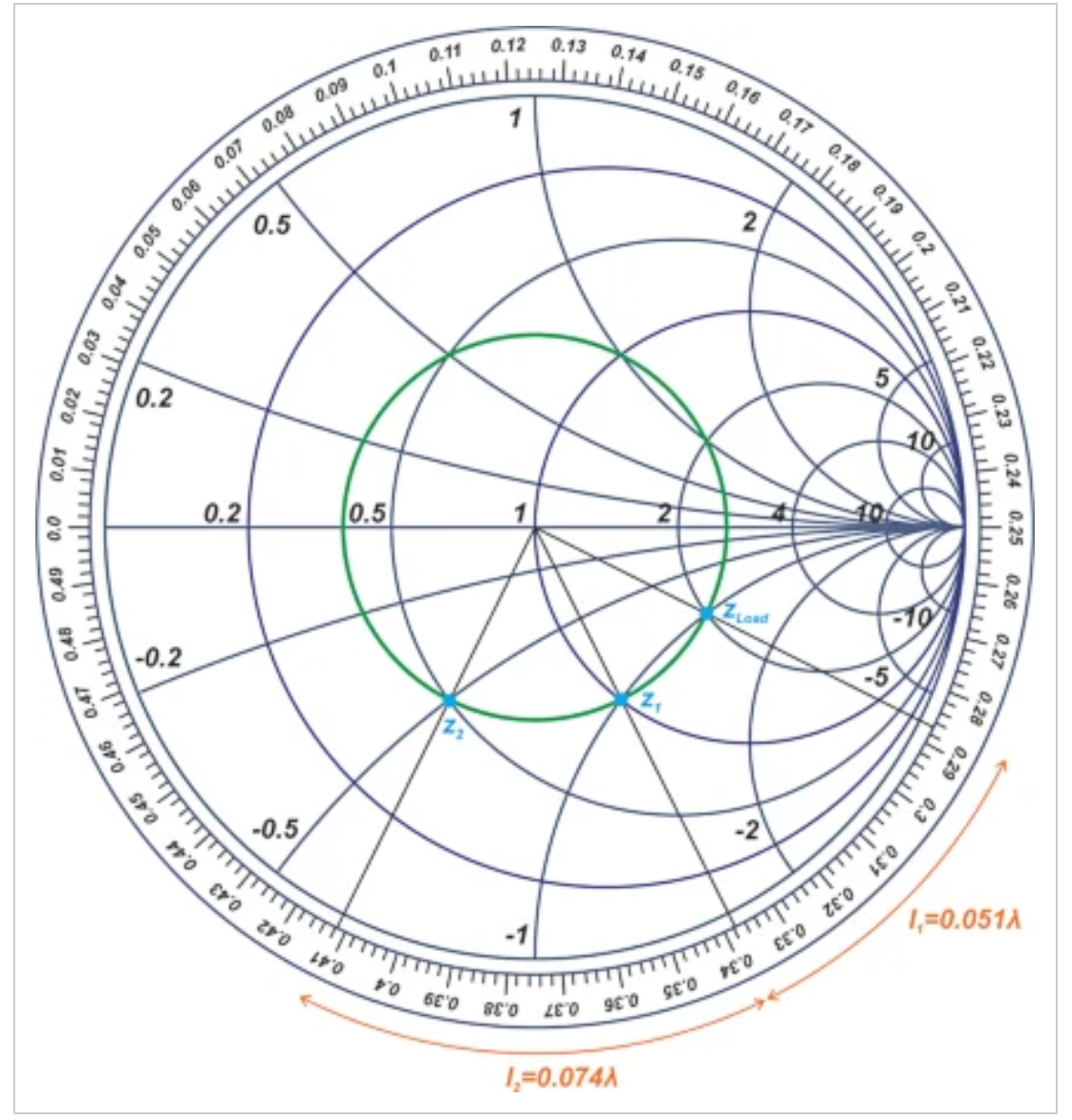
图5史密斯圆图显示了50Ω的归一化阻抗

我们知道，沿着传输线移动会导致沿着史密斯圆图上的常数|Γ|圆的运动。我们只需要确定正确的运动方向。请记住，远离终端会产生顺时针旋转（相对于终端），靠近终端会导致逆时针旋转。

如上图所示，z1在波长尺度上对应于约0.338λ。对于z2，我们又偏离了zLoad 0.074λ。因此，z2在波长尺度上对应于0.338λ+0.074λ=0.412λ，如图5所示。另一方面，要定位zLoad，我们应该逆时针方向前进，这将我们带到与0.338λ-0.051λ=0.287λ对应的点。从史密斯圆图中，我们得到ZLoad=50×ZLoad=100-j50Ω和Z2=50×Z2=25-j25Ω。

示例3：查找ZLoad和Z2

在下图中，我们有Z1=50-j50Ω，l1=0.051λ，l2=0.574λ。找到ZLoad和Z2。

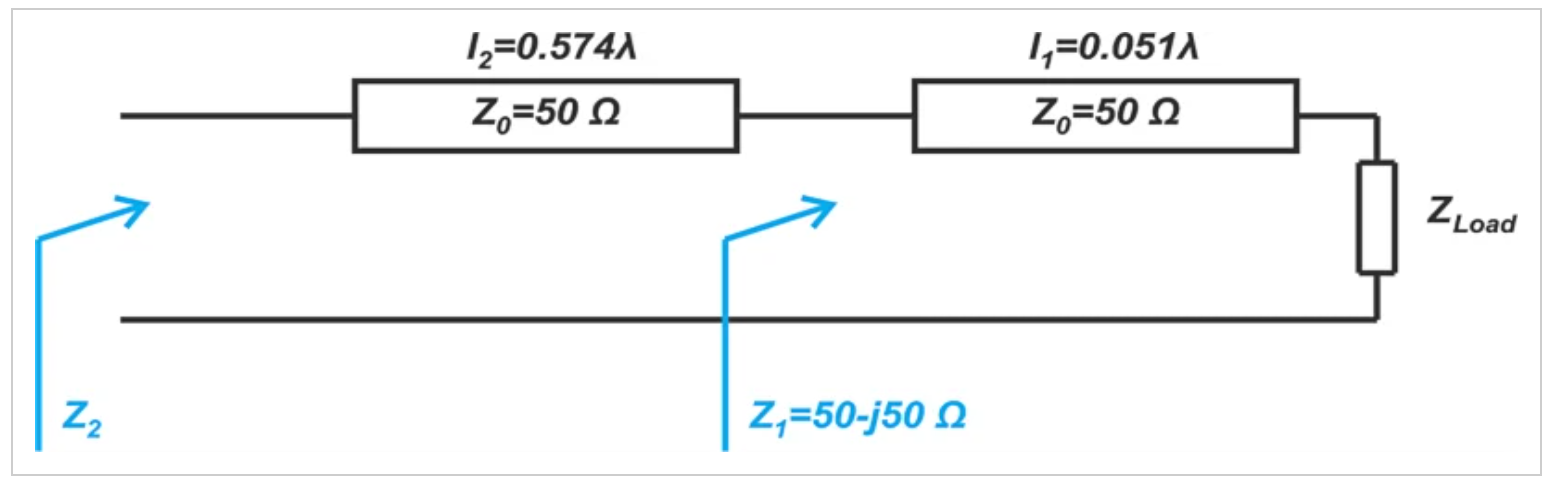
图6显示需要找到ZLoad和Z2的图表

由于观察线路的输入阻抗每半个波长重复一次，我们可以推断出0.574λ的线路等效于0.074λ的线路。考虑到这一点并使用前一个例子的结果，我们得到ZLoad=50×ZLoad=100-j50Ω和Z2=50×Z2=25-j25Ω。

发电机和负载尺度的波长

许多教科书以及商业史密斯圆图都包括两个波长标度，一个标记为“朝向发生器的波长”，另一个标记是“朝向负载的波长”（下图7）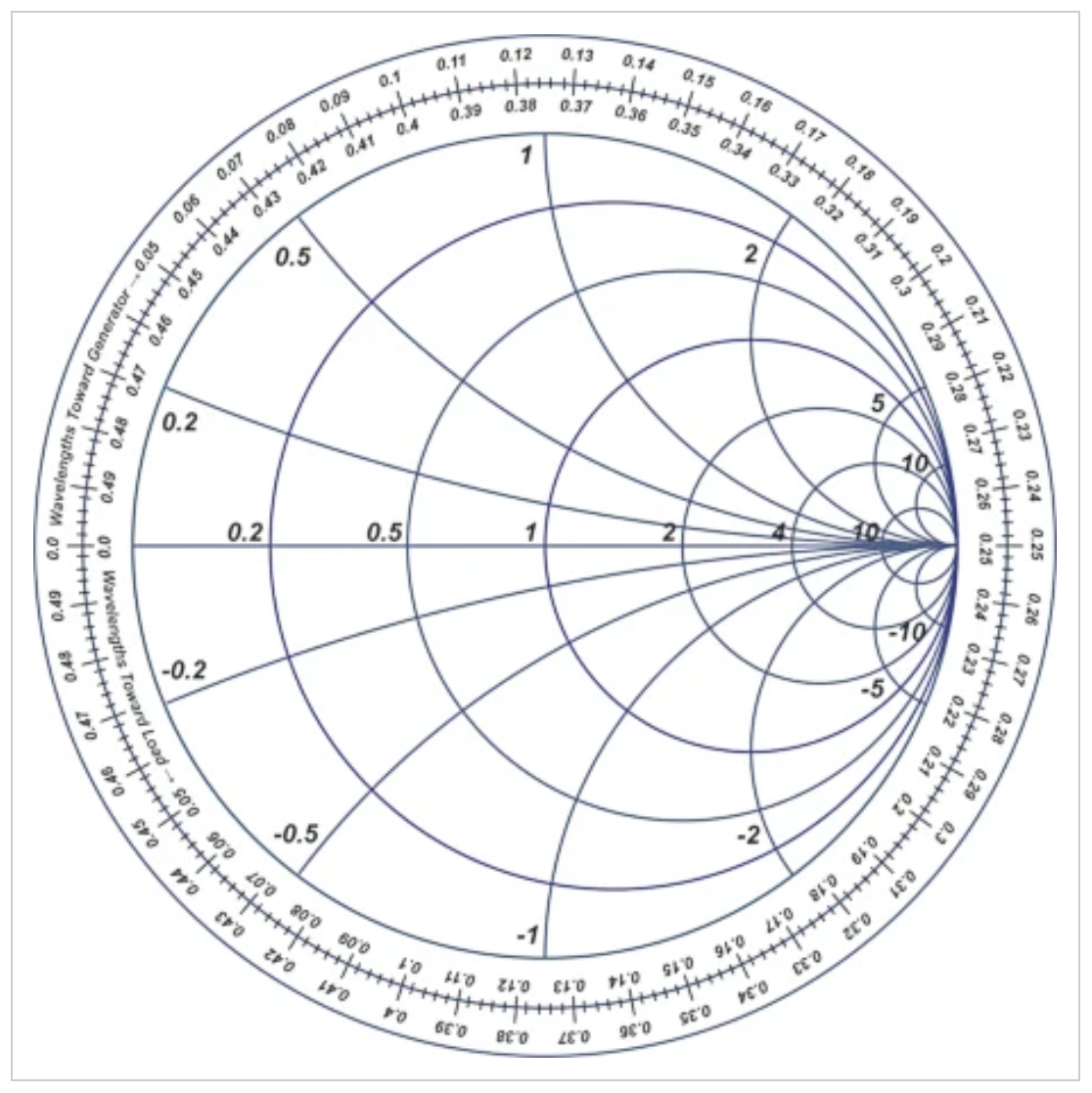 

图7示例史密斯圆图显示了“朝向生成器的波长”和另一个“朝向负载的波长”标签

“朝向发电机的波长”标度沿顺时针方向增加，而“朝向负载的波长”的标度沿逆时针方向增加。使用“发电机”和“负载”术语有时会引起混淆。为了避免这种混淆，请记住，终端的实际功能——即它是否是源阻抗——并不重要。当我们在终端上添加一条串联传输线时，该线的输入阻抗和反射系数是通过史密斯圆图上的顺时针旋转得到的。另一方面，当我们缩短线的长度并接近终点时，旋转是逆时针的。

传输线作为阻抗匹配组件

我们现在可以很好地引入我们在前面章节中提到的基于传输线的阻抗匹配。例如，假设我们需要将ZL=100+j50Ω转换为50Ω。负载阻抗ZL实际上与我们在上述示例1中使用的值相同。图9中再现了图2的史密斯圆图，以及一些额外的细节。

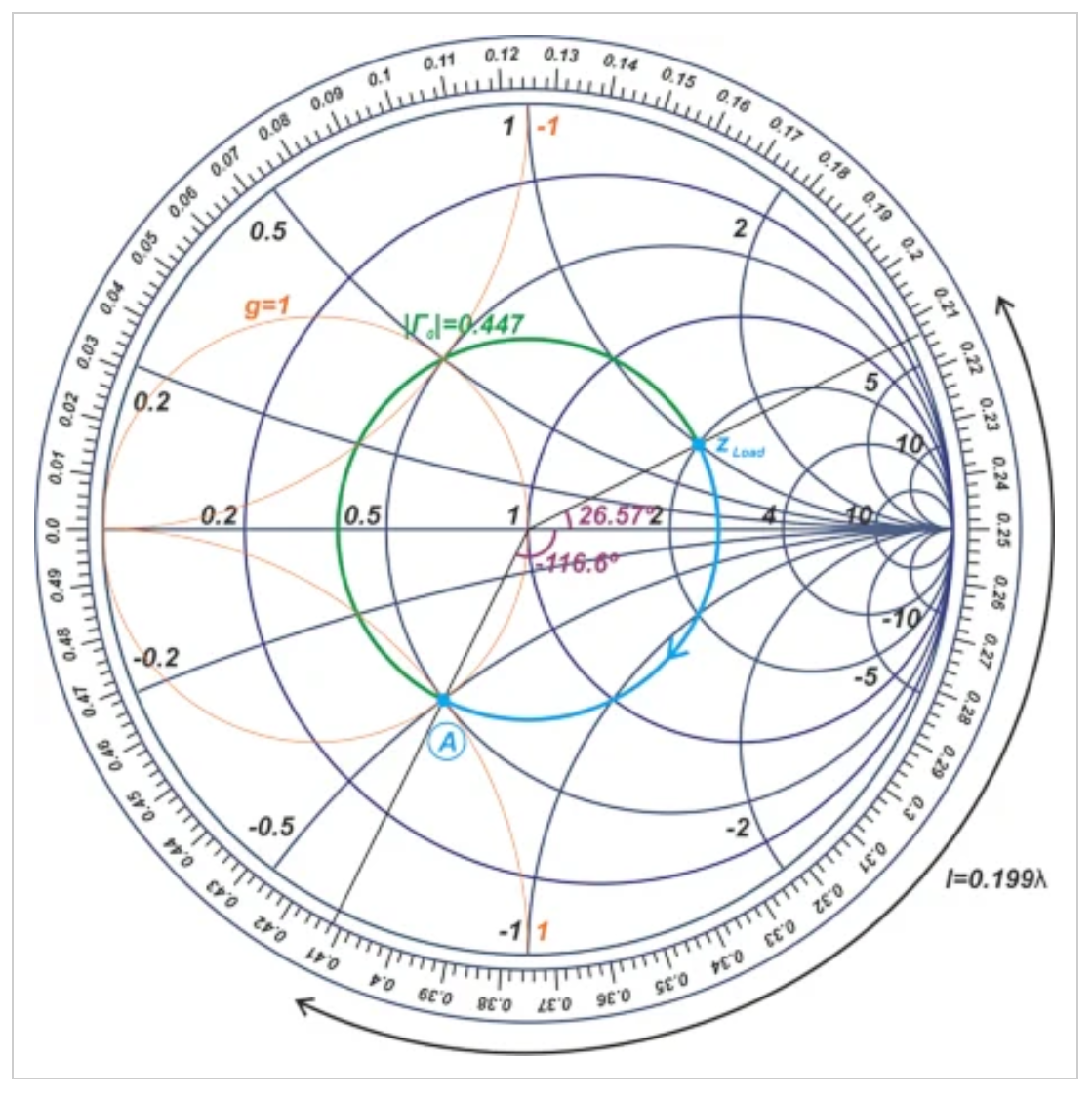
图9图2中的史密斯圆图，带有其他详细信息

在这个例子中，故意选择线路的长度，使我们从负载阻抗zLoad移动到g=1恒定电导圆上的点a。该线的电气长度为71.585°，对应于0.412λ-0.213λ=0.199λ的长度（从波长尺度来看）。

由于我们在g=1的圆上，我们可以在线的输入中添加一个具有适当电纳的平行分量，并沿着g=1的圆周移动到史密斯圆图的中心（图10）。

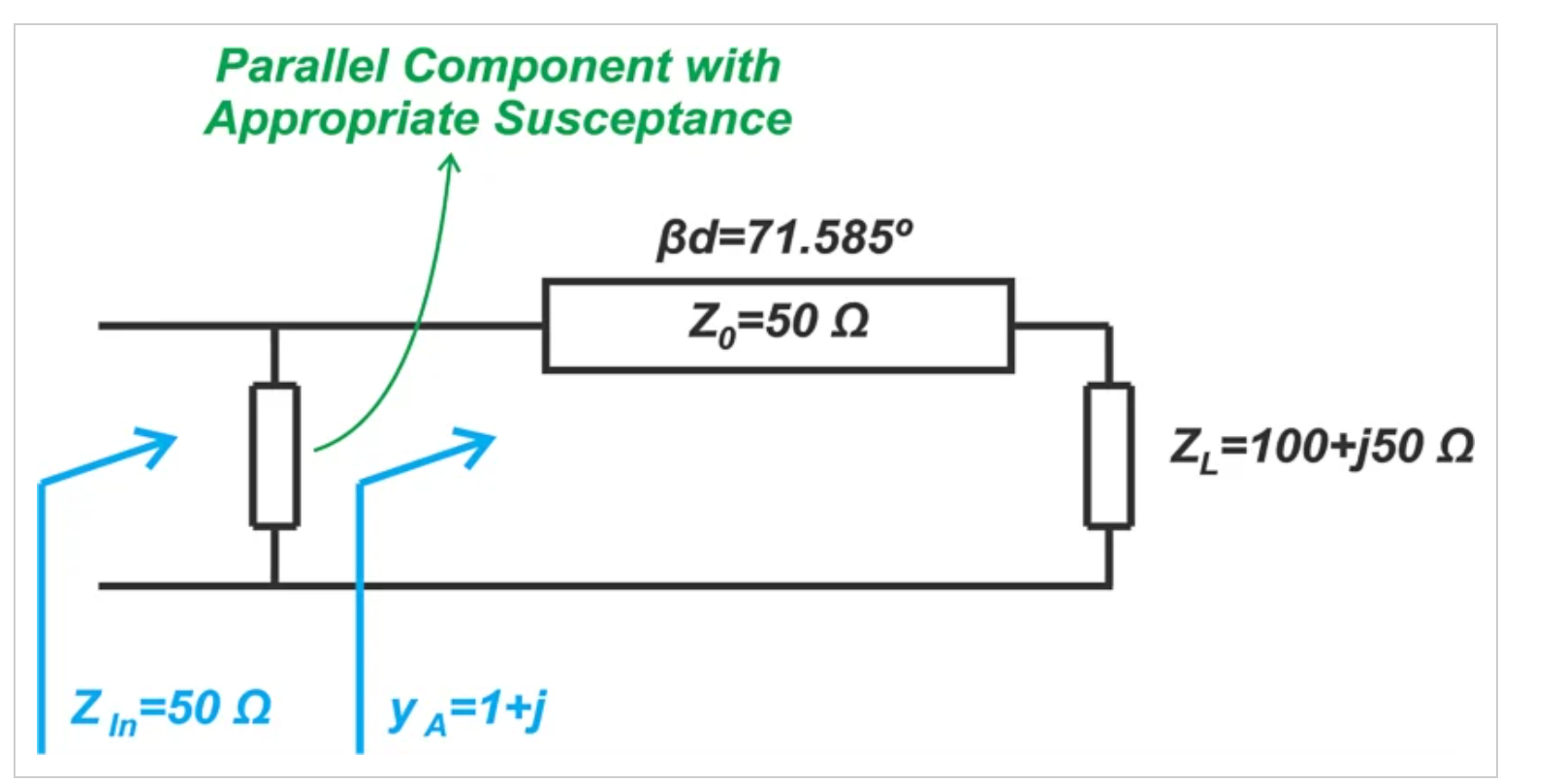
图10显示添加并行组件的示意图

从图9中可以看出，点A处的归一化导纳为yA=1+j。我们需要一个归一化电纳为-j的平行元素才能到达史密斯圆图的中心。一种选择是使用并联电感器。如果感兴趣的频率为1 GHz，则电感器值如下计算：

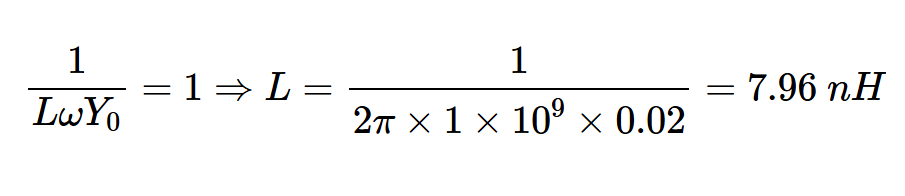
我们可以再次利用传输线的阻抗变换特性，而不是使用集总元件。例如，电气长度为45°的短路线路，对应长度为λ/8，可以产生所需的归一化电纳-j。如图11所示。

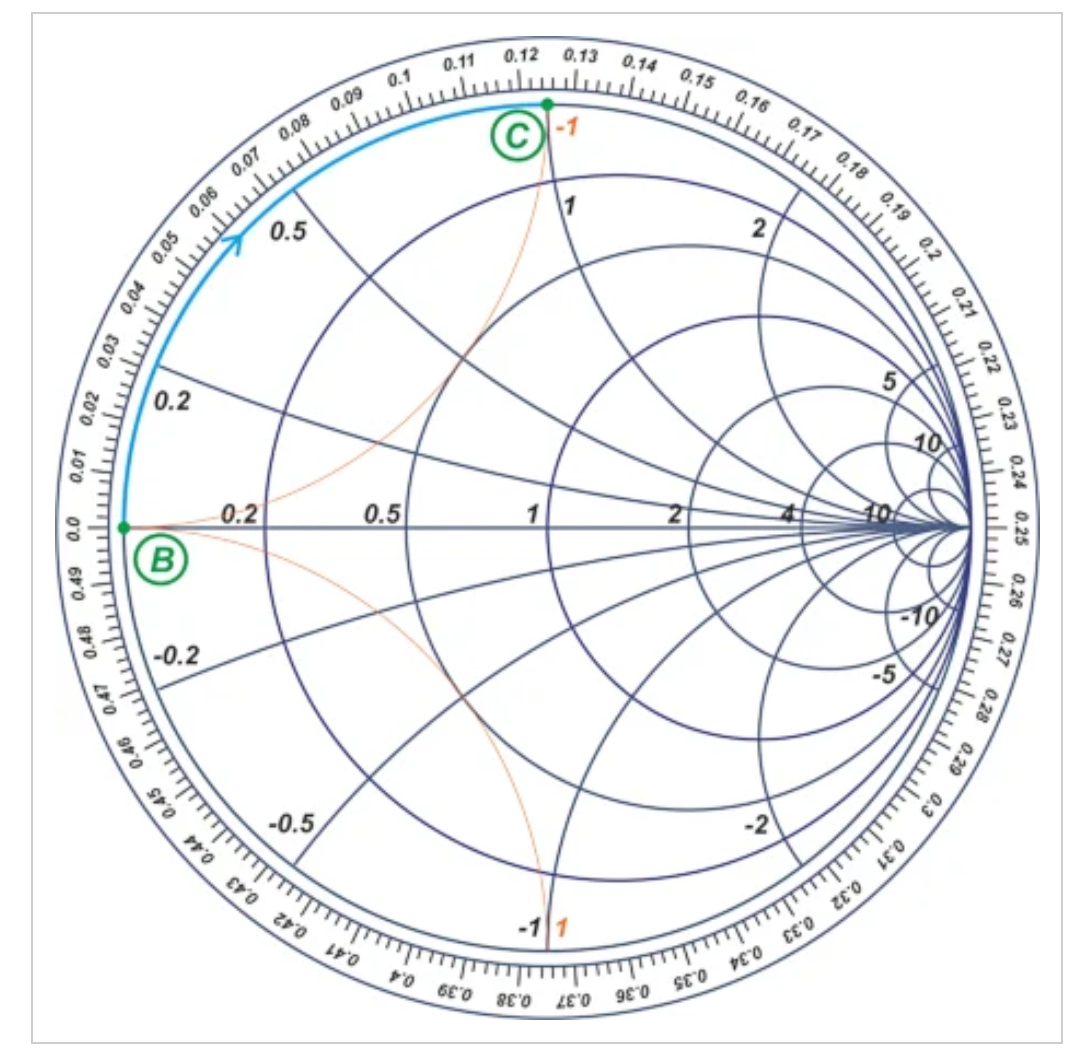
图11史密斯圆图显示了45°的对应关系，以产生所需的归一化电纳

在上图中，点B对应于短路负载。λ/8线产生90°顺时针旋转，根据需要将我们移动到点C，该点的归一化导纳为-j。最终的匹配电路如图12所示。

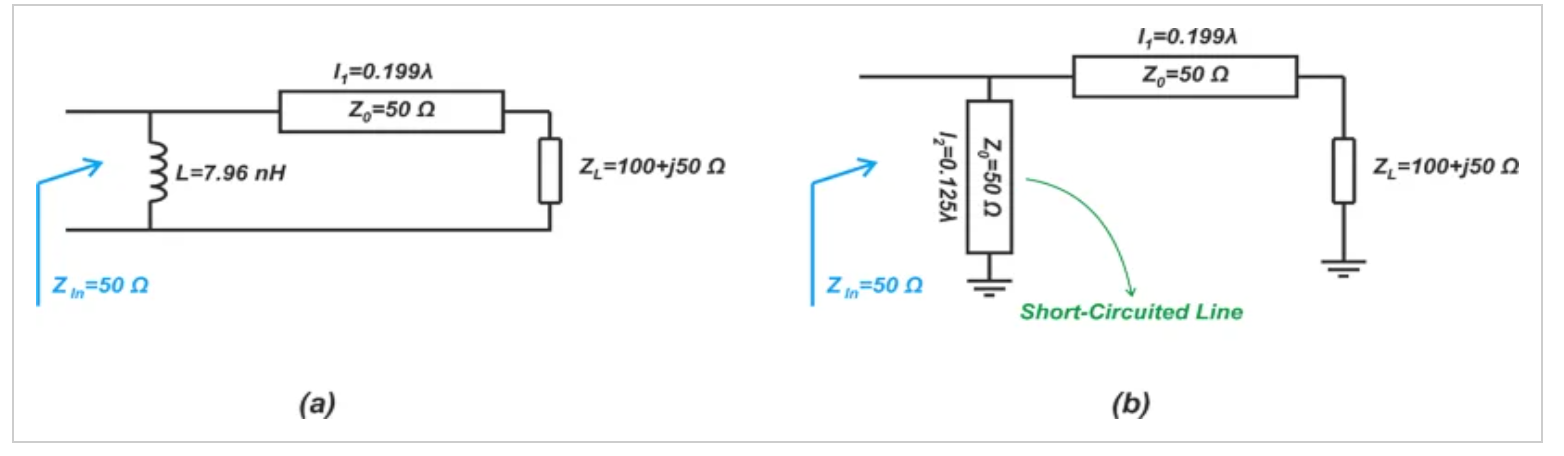
图12与图11史密斯圆图结果相匹配的电路图

基于传输线的阻抗匹配总结

与集总匹配网络不同，基于传输线的阻抗匹配更适合高频应用。适当选择的串联线与并联短截线的组合可以将任意阻抗转换为另一个所需值。在这篇文章中，我们通过一个例子介绍了这种技术。在下一篇文章中，我们将继续这个主题，并研究应用这种技术的不同方法。