氧化锌压敏电阻8/20μS脉冲电流下的伏安特性曲线分析
1 引言
本文引用地址:https://www.eepw.com.cn/article/177241.htm氧化锌压敏电阻器在8/20μS脉冲电流下的伏安特性,在以往有很多研究[1-4],普遍认为:压敏电阻器在8/20μS脉冲电流下,电流峰值和电压峰值不同时到达,电压峰值早于电流峰值,上升沿的伏安特性曲线和下降沿的伏安特性曲线不相重合且形成回线特征;有的认为是脉冲电流激发的空穴滞后效应[3],有的认为是电致伸缩或热效应引起的滞后效应[4],有的认为是受冲击电流和电流变化率影响[2]。
回线特征自然联想到电感效应。虽然以往的试验采用各种方法减少或消除压敏电阻器在8/20μS脉冲电流测试中的电感,但压敏电阻器的伏安特性回线特征仍然不能被消除。这到底是因为电感无法消除还是回线特征就是压敏陶瓷体的本征特性呢?
其实,因为压敏陶瓷体不可能采用零引出,减小引线长度、采用中空阀片和采用凯文接线法等只能尽可能减小电感,在压敏电阻器冲击测量时电感是无法完全消除的。即使采用零长度引出线将电流通入压敏陶瓷体表面电极,电流也须在表面电极上重新分配到每一点,表面电极的电流通道构成了等效电感。压敏电阻电极等效电感和测试点间的引线电感共同构成压敏电阻器引出电感。引出电感不可消除。引出电感肯定对回线特征有贡献。
本文就是试图对压敏电阻器在8/20μS脉冲电流下伏安特性曲线的回线特征进行半定量的分析,确认回线特征是否压敏陶瓷休的本征特性。
2 建立模型
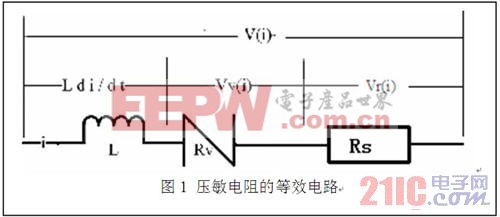
如图1氧化锌压敏电阻在8/20μS脉冲电流下击穿以后的电流区下的等效电路。其中L为压敏电阻的引出电感和陶瓷体等效电感,RV为压敏电阻陶瓷体敏感电阻(含非线性晶界和晶粒),Rs为引出电阻,i为流过压敏电阻器的电流,V(i)为压敏电阻器上的总压降,VV(i)为压敏电阻陶瓷体敏感电阻压降,Vr (i)为引出电阻上的电压降,di/dt为电流随时间的变化率,脉冲电流时di/dt为电流的函数,则电感上的电压降为L di / dt 。
根据等效电路图1,串联电感不能为零,电感的存在一定会在冲击测试时产生伏安特性的回线,上升段电压高于下降段,这和压敏电阻器回线特征很一致。由此提出假设,回线是等效电感引起的,将等效电感作常量看待,压敏陶瓷体的电阻是一个纯可变电阻,引出电阻和压敏陶瓷体的电阻上的电压降只与电流大小有关而与电流时间变化率无关。可以得出:
在8/20μS脉冲电流上升沿,压敏电阻器上的电压可以表示成式(1)
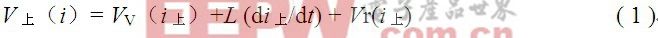
在8/20μS脉冲电流下降沿,压敏电阻器上的电压可以表示成式(2)
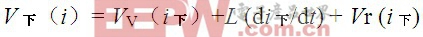 (2)
(2)
在8/20μS脉冲电流下降沿,对应于同一电流值,压敏电阻器陶瓷体上的压降相同,如式(3a); 同时,引出电阻上的电压降相同,如式(3b)。
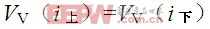 (3a)
(3a)
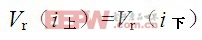 (3b)
(3b)
在8/20μS脉冲电流下降沿,对应于同一电流值,将式(1)和式(2)相减得式(4),上升沿和下降沿对应于同一电流值的等效电感上的上升下降沿电压差,是上升沿和下降沿电流时间变化率差值的函数。在已知等效电感上的上升下降沿电压差与上升沿和下降沿电流时间变化率差值时,就可以计算等效电感值。
V上(i)- V下(i)=L (di上/ dt - di下/dt )= f (di/dt ) ( 4 )
3 实验条件
试验样品为20D101(中压料)、20D620(低压料)、32D560(低压料)和32D101(低压料)各1只,20D产品引线间距10mm、测试点为引线根部和引线约50mm处,32D产品引线间距15mm、 测试点为引线根部;间距10mm、长度125mm平行引线电压降测量。
冲击发生器为SK-20KA,用设备的分流器进行电流取样,直接在压敏电阻器的两引线根部取样电压信号,用TDS102示波器依次显示和测量电流和电压信号。冲击电流波形为8/20μS,峰值为2.0kA和3.0kA。
4 试验结果及分析
4.1 测试数据显示引线上电阻效应不可忽略
图2为测试的压敏电阻器在8/20uS冲击下的伏安特性回线特征图的示例,曲线显见呈现明显的回线特征,上升沿电压大于下降沿。图3和图4为示波器捕获的电流和电压波形,电压峰值先于电流峰值,不像简单的电感,在电流峰值处电流时间变化率为零,但显示此时平行引线首尾测试点间的电压不相等,过了峰值电流后才达到相等的电压值,将各测试中电流峰值点与电引线上电压为零的时间差、零电压时的电流值列于表1,可以很确定地说,引线上的电阻效应不可忽略。
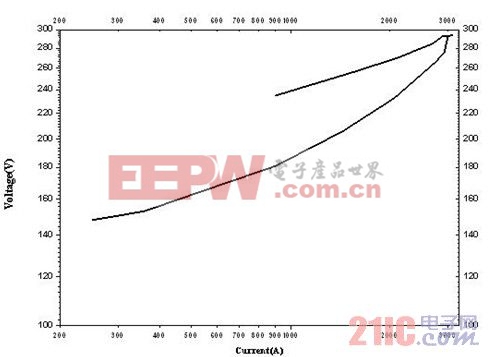
图2 产品在3.1KA的8/20μS脉冲电流下的伏安特性部分曲线
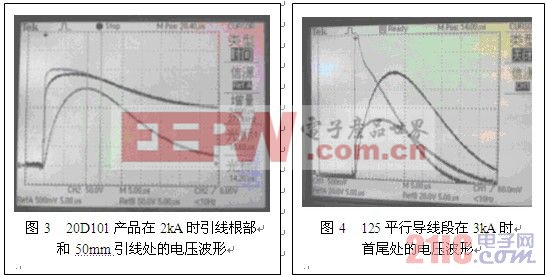
表1 8/20μS脉冲电流下产品引线及纯引线首尾处电压相等点与电流峰值的差别
试品 | 冲击电流峰值 | 导线零电压点电流值 | 电流峰值点与导线 |
125mm导线 | 2 | 1.84 | 4.2 |
3 | 2.9 | 2.8 | |
20D101 | 2 | 1.9 | 3 |
3 | 2.88 | 3.2 | |
20D620 | 2 | 1.96 | 3.4 |
3 | 2.95 | 1.6 |
表2为理论计算的直径1mm的平行双铜导线电阻以及对应冲击电流时的电压降,从数据显示,引出电阻的影响确实不可忽略。
表2 直径1mm的平行双铜导线电阻的理论计算结果
电流 mA | 电阻 | 电压降V | ||
mΩ | @0.9kA | @2kA | @3kA | |
10 | 0.446 | 0.401 | 0.892 | 1.338 |
50 | 2.23 | 2.007 | 4.460 | 6.69 |
125 | 5.575 | 5.018 | 11.150 | 16.725 |
4.2 从测试数据中计算出等效电感值
根据测试得到对应电流的上升沿和下降沿电流变化率和电压差值,按照式(4)计算出125mm平行双铜导线、20D101的引线及被银陶瓷体、20D620的引线及被银陶瓷体的等效电感值,分别列于表3、表4和表5。
表3 125mm平行双铜导线的试验推导电感值
2kA | 电流A | 900 | 1200 | 1500 | 1800 | 2000 |
上升沿电流变化率A/μS | 368 | 272 | 192 | 100 | 0 | |
下降沿电流变化率A/μS | -65.6 | -73.6 | -76.8 | -60.8 | 0 | |
上升下降沿电流变化率差A/μS | 433.6 | 345.6 | 268.8 | 160.8 | 0 | |
上升沿电压V | 63.6 | 48.8 | 35.6 | 24.8 | 8.8 | |
下降沿电压V | -5.6 | -6 | -4 | -0.8 | 8.8 | |
上升下降沿电压差V | 69.2 | 54.8 | 39.6 | 25.6 | 0 | |
等效电感nH | 159.6 | 158.6 | 147.3 | 159.2 |
| |
3kA | 电流A | 900 | 1500 | 2000 | 2500 | 3000 |
上升沿电流变化率A/μS | 580 | 420 | 328 | 220 | 0 | |
下降沿电流变化率A/μS | -88 | -120 | -126 | -108 | 0 | |
上升下降沿电流变化率差A/μS | 668 | 540 | 454 | 328 | 0 | |
上升沿电压V | 93.8 | 71 | 58 | 42.8 | 9.6 | |
下降沿电压V | -10 | -12 | -12.8 | -8.4 | 9.6 | |
上升下降沿电压差V | 103.8 | 83 | 70.8 | 51.2 | 0 | |
等效电感nH | 155.4 | 153.7 | 155.9 | 156.1 |
|
表4 20D101的引线及被银陶瓷体的试验推导电感值
2kA | 电流A | 900 | 1200 | 1500 | 1800 | 2000 |
上升沿电流变化率A/μS | 368 | 272 | 192 | 80 | 0 | |
上升沿电流变化率A/μS | -65.6 | -73.6 | -76.8 | -60.8 | 0 | |
上升下降沿电流变化率差A/μS | 433.6 | 345.6 | 268.8 | 140.8 | 0 | |
根部上升沿电压V | 220 | 227 | 230 | 235 | 234 | |
根部下降沿电压V | 181 | 194 | 207 | 223 | 234 | |
5cm导线处上升沿电压V | 249 | 250 | 249 | 244 | 237 | |
5cm导线处下降沿电压V | 178 | 192 | 205 | 222 | 237 | |
5cm导线的上升沿电压V | 29 | 23 | 19 | 9 | 3 | |
5cm导线的下降沿电压V | -3 | -2 | -2 | -1 | 3 | |
被银瓷片上升下降沿电压差V | 39 | 33 | 23 | 12 | 0 | |
5cm导线上升下降沿电压差V | 32 | 25 | 21 | 10 | 0 | |
被银瓷片电感nH | 89.9 | 95.5 | 85.6 | 85.2 |
| |
5cm导线电感nH | 73.8 | 72.3 | 78.1 | 71.0 |
| |
3kA | 电流A | 900 | 1500 | 2000 | 2500 | 3000 |
上升沿电流变化率A/μS | 580 | 424 | 328 | 220 | 0 | |
上升沿电流变化率A/μS | -88 | -120 | -126 | -108 | 0 | |
上升下降沿电流变化率差A/μS | 668 | 544 | 454 | 328 | 0 | |
根部上升沿电压V | 232 | 250 | 260 | 268 | 268 | |
根部下降沿电压V | 174 | 198 | 218 | 238 | 268 | |
5cm导线处上升沿电压V | 275 | 281 | 285 | 288 | 272 | |
5cm导线处下降沿电压V | 170 | 191 | 212 | 234 | 272 | |
5cm导线的上升沿电压V | 43 | 31 | 25 | 20 | 4 | |
5cm导线的下降沿电压V | -4 | -7 | -6 | -4 | 4 | |
被银瓷片上升下降沿电压差V | 58 | 52 | 42 | 30 | 0 | |
5cm导线上升下降沿电压差V | 47 | 38 | 31 | 24 | 0 | |
被银瓷片电感nH | 86.8 | 95.6 | 92.5 | 91.5 |
| |
5cm导线电感nH | 70.4 | 69.9 | 68.3 | 73.2 |
|
表5 20D620的引线及被银陶瓷体的试验推导电感值
2kA | 电流A | 900 | 1200 | 1500 | 1800 | 2000 |
上升沿电流变化率A/μS | 368 | 272 | 192 | 80 | 0 | |
上升沿电流变化率A/μS | -65.6 | -73.6 | -76.8 | -60.8 | 0 | |
上升下降沿电流变化率差A/μS | 433.6 | 345.6 | 268.8 | 140.8 | 0 | |
根部上升沿电压V | 186 | 197 | 205 | 211 | 214 | |
根部下降沿电压V | 157 | 172 | 185 | 201 | 214 | |
5cm导线处上升沿电压V | 212 | 218 | 220 | 220 | 217 | |
5cm导线处下降沿电压V | 155 | 168 | 182 | 200 | 217 | |
5cm导线的上升沿电压V | 26 | 21 | 15 | 9 | 3 | |
5cm导线的下降沿电压V | -2 | -4 | -3 | -1 | 3 | |
被银瓷片上升下降沿电压差V | 29 | 25 | 20 | 10 | 0 | |
5cm导线上升下降沿电压差V | 28 | 25 | 18 | 10 | 0 | |
被银瓷片电感nH | 66.9 | 72.3 | 74.4 | 71.0 |
| |
5cm导线电感nH | 64.6 | 72.3 | 67.0 | 71.0 |
| |
3kA | 电流A | 900 | 1500 | 2000 | 2500 | 3000 |
上升沿电流变化率A/μS | 620 | 424 | 328 | 220 | 0 | |
上升沿电流变化率A/μS | -88 | -120 | -126 | -108 | 0 | |
上升下降沿电流变化率差A/μS | 708 | 544 | 454 | 328 | 0 | |
根部上升沿电压V | 196 | 216 | 231 | 244 | 246 | |
根部下降沿电压V | 153 | 177 | 198 | 219 | 246 | |
5cm导线处上升沿电压V | 237 | 247 | 255 | 259 | 250 | |
5cm导线处下降沿电压V | 148 | 172 | 192 | 214 | 250 | |
5cm导线的上升沿电压V | 41 | 31 | 24 | 15 | 4 | |
5cm导线的下降沿电压V | -5 | -5 | -6 | -5 | 4 | |
被银瓷片上升下降沿电压差V | 43 | 39 | 33 | 25 | 0 | |
5cm导线上升下降沿电压差V | 46 | 36 | 30 | 20 | 0 | |
被银瓷片电感nH | 60.7 | 71.7 | 72.7 | 76.2 |
| |
5cm导线电感nH | 65.0 | 66.2 | 66.1 | 61.0 |
|
4.3 用试验推导出引线电感是合理的方法
表6是用式(5)[5]的方法计算的引线理论电感值和试验推导出的等效引线电感比较。
(5)
表6 理论计算的引线电感值和试验推导出的等效引线电感比较
理论计算电感 | 产品 | 125mm导线 | 20101 | 20620 |
间距a mm | 10.3 | 12.2 | 12.2 | |
引线直径d mm | 1 | 1 | 1 | |
引线长度l mm | 125 | 56 | 50 | |
理论计算电感nH | 150 | 71.2 | 63.5 | |
2kA推导电感 | 均值nH | 156.2 | 73.8 | 68.7 |
极差比率% | 7.86% | 9.62% | 11.29% | |
和理论偏差率% | 4.11% | 3.68% | 8.23% | |
3kA推导电感 | 均值nH | 155.3 | 70.4 | 64.6 |
极差比率% | 1.54% | 6.94% | 8.06% | |
和理论偏差率% | 3.52% | -1.10% | 1.65% |
从表6可以看出,在合理的误差范围内,引线电感的理论计算值和试验推导值非常接近,引线电感为常数,用试验推导出等效电感值的方法是可行的方法。
4.4 压敏电阻器披银陶瓷体的等效电感是常数
将表4和表5中试验推导的20D101和20D620的压敏电阻器披银陶瓷电阻体的等效电感值列于表7,显然在合理的试验误差范围内,披银陶瓷体的冲击等效电感是一个常数。
表7 试验推导的20D产品披银陶瓷体等效电感
产品 | 2kA试验数据 | 3kA试验数据 | ||
等效电感平均值nH | 极差比率 | 等效电感平均值nH | 极差比率 | |
20D101 | 89.1 | 11.52% | 91.6 | 9.57% |
20D620 | 71.2 | 10.57% | 70.3 | 22.02% |
4.5 陶瓷体具有很大的等效电感
披银陶瓷体等效电感,包含陶瓷体等效电感的电极等效电感。将测试的32D560产品和32D101产品的上升沿和下降沿电压差作比较,32D101和32D560披银陶瓷体等效电感与厚度的比较结果列于表8。20D101和20D560披银陶瓷体等效电感与厚度的比较列于表9。由表8显示,32D101是32D560厚度的1.25倍,前者披银陶瓷体的等效电感是后者的1.16倍,20D101的厚度是20D620厚度的0.76倍,而前者的披银陶瓷体的等效电感是后者的1.28倍。
以上电感与陶瓷体厚度的不对应关系说明,陶瓷体厚度不是披银陶瓷体等效电感的主要影响因素。可以作这样的解释,陶瓷厚度是形成电极等效电感的因素,将电极包围的面积和5cm导线包围的面积相比较没有超过1/20,是可以忽略不计的,这样电极等效电感会小于5nH,当然在70nH以上的陶瓷体等效电感中确实不算什么,而这么大的披银陶瓷体等效电感与产品的压敏电压呈明显的正相关,压敏电压与晶界数量成正比。说明披银陶瓷体等效电感主要来源于晶界,所以披银陶瓷体的等效电感只有很少一部分来源于电极等效电感,来源于晶界的陶瓷体等效电感远大于电极等效电感。
由此可以说明,压敏陶瓷体有很大的冲击等效电感,这一等效电感会引起压敏电阻器在8/20μS冲击电流时的伏安特性回线特征,回线特征是压敏陶瓷体的本征特性。即使完全消除电感,回线特征也无法消除。
表8 32D101和32D560披银陶瓷体等效电感与厚度的比较
产品 | 32D101 | 32D560 | 101与560的 | 101与561的 | |
电流A | 披银瓷片上升下降沿电压差V | ||||
2kA | 900 | 37 | 32 | 1.16 | 1.25 |
1200 | 32 | 27 | 1.19 | ||
1500 | 26 | 22 | 1.18 | ||
1800 | 17 | 15 | 1.13 | ||
比率均值 | 1.16 | ||||
3kA | 900 | 55 | 46.5 | 1.18 | |
1500 | 50 | 42 | 1.19 | ||
2000 | 42 | 36 | 1.17 | ||
2500 | 30 | 27 | 1.11 | ||
比率均值 | 1.16 | ||||
表9 20D101和20D560披银陶瓷体等效电感与厚度的比较
产品 | 20D101 | 20D620 | 101与620的 | 101与621的 |
电流A | 被银瓷片推导平均等效电感值nH | |||
2kA | 89.1 | 71.2 | 1.25 | 0.76 |
3kA | 91.6 | 70.3 | 1.30 | |
5 结论
氧化锌压敏电阻在8/20μS脉冲电流下的伏安特性,呈回线特征是压敏陶瓷的本征特性,压敏陶瓷本身在8/20μS脉冲电流下的具有常数等效电感,与晶界数和瓷料有关,引起伏安特性的回线特征。
参考文献
[1] 梁毓锦. 金属氧化物非线性电阻在电力系统中的应用.武汉:华中理工大学出版社,1993.
[2] 吴维韩,何金良,高玉明等.清华大学学术专著: 金属氧化物非线性电阻特性和应用.北京:清华大学出版社,1998.
[3] 孙丹峰,季幼章,姚学玲,陈景亮,张俊峰等.氧化锌压敏电阻8/20us冲击电流下的伏安特性.半导体器件应用 中国电子学会敏感技术分会第十四届电压敏学术年会论文, 2007:1~5
[4] 张俊峰,夏波,孙丹峰等.氧化锌压敏电阻老化机理再探索.半导体器件应用 中国电子学会敏感技术分会第十六届电压敏学术年会论文专刊,2009:68~72
[5] [苏联]海特维西.电感计算. 北京:国防工业出版社. 1960.■
光敏电阻相关文章:光敏电阻工作原理
基尔霍夫电流相关文章:基尔霍夫电流定律
脉冲点火器相关文章:脉冲点火器原理


评论