双稳态电路
工作原理
图一为双稳态电路,它是由两级反相器组成的正反馈电路,有两个稳定状态,或者是BG1导通、BG2截止;或者是BG1截止、BG2导通,由于它具有记忆功能,所以广泛地用于计数电路、分频电路和控制电路中,
原理,图2(a)中,设触发器的初始状态为BG1导通,BG2截止,当触发脉冲方波从1端输入,经CpRp微分后,在A点产生正、负方向的尖脉冲,而只有正尖脉冲能通过二极管D1作用于导通管BG1的基极是。ic1减小使BG1退出饱和并进入放大状态,于是它的集电极电位降低,经电阻分压器送到截止管BG2的基极,使BG2的基极电位下降,如果下降幅度足够时,BG2将由截止进入放大状态,因而产生下列正反馈过程(看下列反馈过程时,应注意:在图一的PNP电路中,晶体管的基极和集电极电位均为负值,所以uc1↓,表示BG1集电极电位降低,而uc1↑则表示BG1集电极电位升高,当BG1基极电位降低时,则ic1↑,反之当BG1基极电位升高时,ic1↓
ic1越来越小,ic2越来越大,最后到达BG1截止、BG2导通;接差触发脉冲方波从2端输入,并在t=t2时,有正尖脉冲作用于导通管BG2的基极,又经过正反馈过程,使BG1导通,BG2截止。以后,在1、2端的触发脉冲的轮流作用下,双稳电路的状态也作用相应的翻转,如图一(b)所示。 
图一、双稳态电路
由上述过程可见:(1)双稳态电路的尖顶触发脉冲极性由晶体管的管型决定:PNP管要求正极性脉冲触发,而NPN管却要求负极性脉冲触发。(2)每触发一次,电路翻转一次,因此,从翻转次数的多少,就可以计算输入脉冲的个数,这就是双稳态电路能够计算的原理。
双稳态电路的触发电路形式有:单边触发、基极触发、集电极触发和控制触发等。
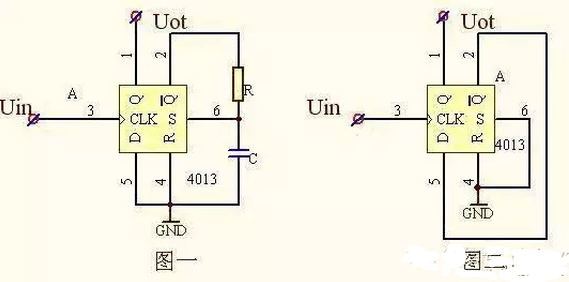
图二给出几种实用的双稳态电路。电路(a)中D3、D4为限幅二极管,使输出幅度限制在-6伏左右;电路(b)中的D5、D6是削去负尖脉冲;电路(C)中的ui1、ui2为单触发,ui为输入触发表一是上述电路的技术指标。 
图二、几种实用的双稳态电路
表一 本文引用地址:https://www.eepw.com.cn/article/259021.htm | 几种双稳态触发器的技术指标 | ||||
图二 | (a) | (b) | (c) | (d) | |
管型 | 二极管 | 2AP3 | 2AP15 | 2AK1C | 2AK17 |
三极管 | 3AX31B | 3AG40 | 3AK20 | 3DK3B | |
信号电平 | “0”(无信号)(V) | 0 | 0 | 0 | +6 |
“1”(有信号)(V) | -6 | -6 | -9 | 0 | |
工作频率(KHz) | 10 | 600 | 1000 | 8000 | |
抗干扰电压(V) | ≥1 | ≥1.5 | ≥2 | 0.8-1 | |
触发灵敏度(V) | ≤4 | ≤4.8 | ≤7 | 2.5 | |
输出端的吸收能力(mA) | ≤4 | ≤6.7 | ≤2 | 10 | |
输出端的发射能力(mA) | ≤44 | ≤12 | ≤12 | 7 | |
输出脉冲的上升时间(μs) | 2 | ≤0.30 | ≤0.1 | ≤0.1 | |
输出脉冲的下降时间(μs) | 2 | ≤0.36 | ≤0.15 | ≤0.1 | |
对β值的要求 | >50 | 50-80 | 60-90 | >50 | |
元件参数的允许化 | △β<10,±5% | △β<10,±5% | △β<10,±5% | △β<10,±5% | |
电源电压的波动范围 | ±5% | ±5% | ±5% | ±5% | |
工作温度范围(℃) | 0-40 | -10-55 | -20-50 | -10-55 | |
二、双稳态电路的设计

图三、双稳态的设计电路
双稳态设计电路见表二
表二 | 双稳态电路的设计公式及计算实例 | |
要求 | (1)输出幅度Um=6V,(2)上升时间,tr≤100nS | |
步骤 | 计算公式 | 计算实例 |
选择晶体管 | 若工作频率高时,应选用高速硅开关管 | 现选3DK,β=50 |
选择电源电压 | 图3为设计电路,故应确定ED、EC、EB | ∵采用箝位电路,故选ED≈Um |
计算Rc | Rc<Ec/ED tr/CL | 现设CL=180pF |
计算Rk、RB | 为保证可靠截止,应满足: | 现选Uces=0.4V,Ubeo=0.2V |
选择CrRr | RrCr≤1/2fmax,通常Cr为几十pF | 现选Cr=51pF |
选择加速电容CK | 对合金管CK为几百pF对高频外延管CK为几十pF | 现选Ck=51pF |




评论