变压器局部放电超声定位中的自适应优化算法
(6) 进行牛顿迭代,计算▽F(Xk),若‖▽F(Xk)‖≤ε则停,输出Xk;否则,进行(7);
(7) 计算Sk=-[▽2F(Xk)]-1*gk;
(8) 一维搜索:min F(Xk+λSk) = F(Xk+λkSk),令Xk+1 = Xk+λkSk,k=k+1,进行(6)。
2.2 体元分割法选取初始点
算法中,开始迭代前要对未知向量取合适的初始点,初始点的选取往往关系到算法的成败.但将本算法集成到系统软件中时,需要自动选择高效率的初始点。考虑这样一种方法,将变压器分割成大小相同的体积元,体积元的个数可以是几十个甚至几百个,以每个体元的几何中心作为初始点依次进行迭代,迭代结束后.再根据所有体元的迭代结果进行比较,判断出整个变压器中的最优点。
2.3 算法分析
本算法将最速下降法和牛顿法相结合,根据体元分割选取初始点,迭代开始后。借助最速下降法全局收敛的特性,在梯度向量出现振荡现象之前完成了初步寻优过程,然后采用牛顿法进行精确寻优,牛顿法收敛速度快,在10步之内,迭代结果即可满足精度要求。3 组合算法在电力变压器局部放电点定位中的应用
在山西运城供电公司的变压器局部放电在线检测项目中,应用了该算法,以下为现场检测情况。
现场一检测情况:
变压器规则(长×宽×高):1.2 m×0.8 m×1.0 m;
实际放电点坐标:S(0.5,0.4,0.4);
传感器坐标:R1(0.6,0.0,0.5),R2(0.0,0.4,0.5),R3(0.6,0.4,1.0),R4(1.2,0.4,0.5),R5(0.6,0.8,0.5);
参考点时刻:t1=0.000 303 05 s;
接收时延:d1=[0.000 364 22;0.000 434 48;0.000 505 08;0.000 128 6]一t1。
体元个数:5×5×5。
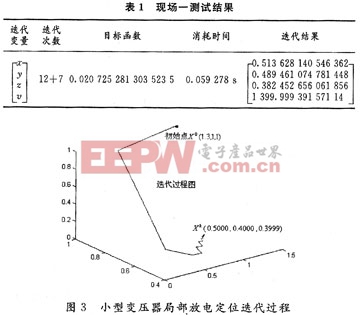
现场二检测情况:
变压器规则(长×宽×高):5 m× 3 m×4 m;
实际放电点坐标:S(4.5,2.6,3.7);
接收端坐标:R1(2.5,0.0,2.0),R2(2.5,1.5,4.0),R3(5.0,1.5,2.O),R4(2.5,3.0,2.0),R5(0,1.5,2.0);
参考点时刻:t1=0.002 6 S;
接收时延:d1=[0.001 6;0.001 5;0.001 9;0.003 524 69]一t1。
体元个数:5×5×5。

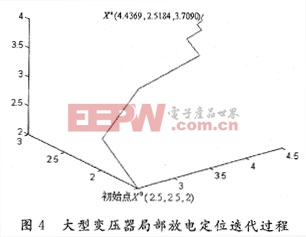
4 结 语
现场检测体现了混合算法的优越性,主要有:








评论