逻辑代数的化简算法

逻辑代数的化简算法

观察函数

1.该函数有四个逻辑变量，可表示成

Y=f(A、B、C、D)

2.该函数有三个乘积项：第一项有四个因子——四个变量在乘积项中都出现了。第二项有三个因子——缺少变量B（或）。第三项缺少变量C、D（或、）。

3.第一个乘积项是A、B、C、D的一个最小项，其余二项均不是A、B、C、D的最小项。

最小项：n个逻辑变量A1、A2、…… An组成的逻辑系统中含n个因子的乘积项——每个变量（或）在乘积项中只出现一次，称这样的乘积项为最小项。

两个逻辑变量A、B有22＝4个最小项，分别是：、、、。

三个逻辑变量A、B、C有23＝8个最小项，分别是：、、、、、、、。

四个逻辑变量A、B、C、D有24＝16个最小项。

练习：写出A、B、C、D的十六个最小项。

最小项的性质：

（1）对变量的任意一组取值，只有一个最小项为1，其余最小项全为0。二变量A、B的最小项为：、、、。对A、B的任意一组取值：

A=0 B=0 =1 其余三项全为0，即＝＝＝0

A=0 B=1 = 1 其余三项全为0

A=1 B=0 = 1 其余三项全为0

A=1 B=1 = 1 其余三项全为0

（2）全体最小项之和为1。（读者自己证明）

（3）任意两个最小项的乘积为0。

最小项的编号：

三变量A、B、C的八组取值000、001、……111能分别使八个最小项的值为1，又与十进制数0，1……7的二进制数表示相同。用0～7编号八个最小项，记为：m0、m1、m2、m3、m4、m5、m6、m7，则m7＝m111＝，……m4＝m100＝，m0＝m000＝。

练习：读者试写出四变量A、B、C、D的十六个最小项m0、m1……m15。

逻辑函数的最小项之和形式

任何逻辑函数都可化为最小项之和的标准形式

例：将下列函数化为最小项之和的形式

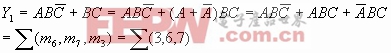
反函数的最小项之和表示

例：求二变量A，B的逻辑函数的反函数。

解一：

解二：列真值表

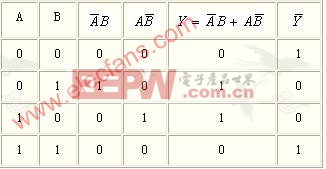
由真值表写出的逻辑表达式

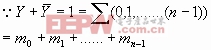(全体最小项之和)

如三变量A,B,C的逻辑函数则必有

结论：在n个变量的逻辑系统中，如果Y为i个最小项之和，则必为余下的（n－i）个最小项之和。

异或运算与同或运算

定义： 称A与B异或，为异或运算符

A与B同或，为同或运算符

显然：

异或与同或互为反函数

由此推得：

即两者相等为0，不相等为1

同或运算则与之相反，且有

同学自己证明并牢记。

例1． 将下列函数化为最简与或式。

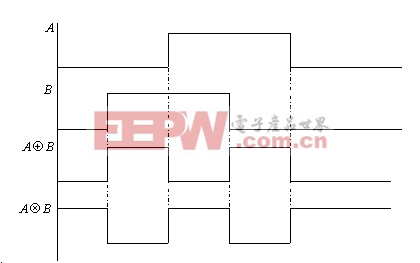
例2． A，B的波形如下图所示,试画出的波形。

最小项的相邻性

任何两个最小项如果他们只有一个因子不同，其余因子都相同，则称这两个最小项为相邻最小项。

显然，m0与m1具有相邻性，而与不相邻，因为他们有两个因子不相同。m3与m4也不相邻，而m3与m2相邻。

相邻的两个最小项之和可以合并成一项，并消去一个变量。如：

卡诺图

卡诺图是美国工程师卡诺（Karnaugh）发明的。用小方块（格）来表示最小项。三变量的卡诺图画八个小方块（格）来表示八个最小项，四变量的卡诺图画十六个小方块来表示十六个最小项。……