17031926319.gif" width=229 v:shapes="_x0000_i1056"> | 如上所述，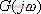
可改写为>
| 式中， |  ， | , |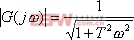
。
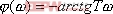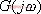称为电路的频率特性。显然，它由该电路的结构和参数决定，与输入信号的幅值和相位无关。
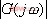是
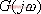的幅值，它表示在稳态时，电路的输出与输入的幅值之比。
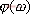是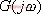
的相角，它表示在稳态时，输出信号与输入信号的相位差。由于
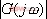和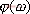
都是输入信号频率ω的函数，故它们分别被称为电路的幅频特性和相频特性。
综上所述，式（5—10）所示频率特性的物理意义是：当一频率为ω的正弦信号加到电路的输入端后，在稳态时，电路的输出与输入之比；或者说，电路的输出与输入的幅值之比和相位之差。
根据式（5—9），R-C电路的稳态输出为
由上式可知，当
时，输出与输入的电压不仅幅值相等，而且相位也完全一致。随着ω的不断增大，输出电压的幅值将不断地衰减，相位也不断地滞后。图5—4示出了该电路的幅频和相频特性。
同样，对于一般的线性定常系统，设输入为一频率为ω的正弦信号，在稳态时，系统的输出具有和输入同频率的正弦函数，但其幅值和相位一般均不同于输入量，且随着输入信号频率的变化而变化。
设线性系统的传递函数具有式（5－2）的形式，已知输入信号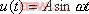
，其拉氏变换 
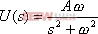，A为常量，则系统的输出为
式中，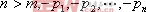 
为
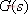的极点。对于稳定系统，这些极点都位于s的左平面，即它们的实部
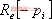均为负值。为简单起见，令
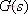的极点均为相异的实数极点，则式（5—12）改写为
其中
、
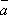和 
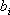(i=1，2，…，n)，均为待定系数。对上式取拉氏反变换，求得
当
时，系统响应的瞬态分量
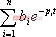趋向零，其稳态分量为
其中
、和 
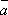由下列两式确定
由于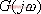
是一个复数向量，因而可表示为
 |
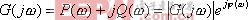技术专区
|
加入技术交流群
评论