4G通信系统中OFDM技术的分析
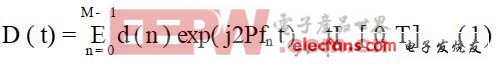
式(1)中:T为码元周期加保护时间;fn为各子载波的频率,可表示为:

式(2)中:f0为最低子载波频率;Ts为码元周期。
在发射端,发射数据经过常规QAM调制形成基带信号。然后经过串并变换成M个子信号,这些子信号再调制相互正交的M个子载波,其中/正交0表示的是载波频率间精确的数学关系,其数学表示为QT0fx(t)fy(t)dt=0,最后相加成OFDM发射信号。实际的输出信号可表示为:

在接收端,输入信号分成M个支路,分别用M个子载波混频和积分,恢复出子信号,再经过并串变换和常规QAM解调就可以恢复出数据。由于子载波的正交性,混频和积分电路可以有效地分离各子载波信道,如下式所示:

式中dc(m)为接收端第m支路子信号。在整个OFDM的工作流程中OFDM与其他技术的主要区别在于其采用的调制/解调技术以及循环前缀的加入这两个环节,下面将对其进行较为详细的分析。
2.2 OFDM调制/解调技术的实现
OFDM系统的调制和解调可以采用离散逆傅立叶变换(IDFT)以及离散傅立叶变换(DFT)来实现,在实际应用中,可以采用更加方便快捷的逆快速傅立叶变换(IFFT)和快速傅立叶变换(FFT)技术来实现调制和解调,这是OFDM的技术优势之一。
先不考虑保护时间,将式(2)代入式(1)可得到如下等式:

由上面的分析可以看出OFDM的调制可以由IDFT实现,而解调可由DFT实现。当系统中的子载波数很大时,可以采用快速傅立叶变换(FFT/IF2FT)来实现调制和解调,以显着地降低运算复杂度,从而在数字信号处理器DSP上比较容易实现,因此能够达到简化4G通信系统中硬件实现的复杂度并减少设备成本的效果,现存的还有诸如矢量变换方式、基于小波变换的离散小波多音频调制方式等,但这些方式与OFDM相比,实现复杂度相对较高,因而一般不会用于4G通信系统。
2.3 循环前缀基本原理
在OFDM系统中,为了最大限度地消除符号间干扰,在每个OFDM符号之间要插入保护间隔,该保护间隔长度Tg一般要大于无线信道的最大时延扩展,这样一个符号的多径分量就不会对下一个符号造成干扰。



评论