无损传输线相位常数和无限带宽的研究
学习如何推导无损传输线的波动方程,并观察其无限带宽和相位常数。
本文引用地址:https://www.eepw.com.cn/article/202410/463787.htm当你开始学习射频设计时,可能会遇到的一个令人恼火的事情是传输线效应。在过去的好日子里,当你在低频板上工作时,电线只是一些互连,现在却变成了一些令人生畏的方程式所描述的复杂组件!起初,这可能看起来很烦人;然而,随着你对输电线路的了解越来越多,你最终可能会把它们看作是因祸得福,并开始意识到所有这些复杂性。由于其“分布式”特性,无损传输线可以提供无限带宽。这与我们对低频电路的直觉形成了鲜明对比。
在本文中,我们将推导无损传输线的波动方程,并研究其无限带宽的显著特征。然而,在此之前,让我们解释一下输电线路的“分布式”性质是什么意思。
集中式与分布式方案
当电路尺寸与电路中最短波长相当时,电线应被视为传输线。这突显了电路元件和互连的两种操作模式之间的界限,即“集中”和分布式模式。在集总方案中,我们处理较低的频率,并且假设电信号以无限快的速度通过电线。术语集总是指我们可以在电路的某些特定区域识别出单独的电容器和电感器。例如,考虑图1所示的无源带通滤波器。
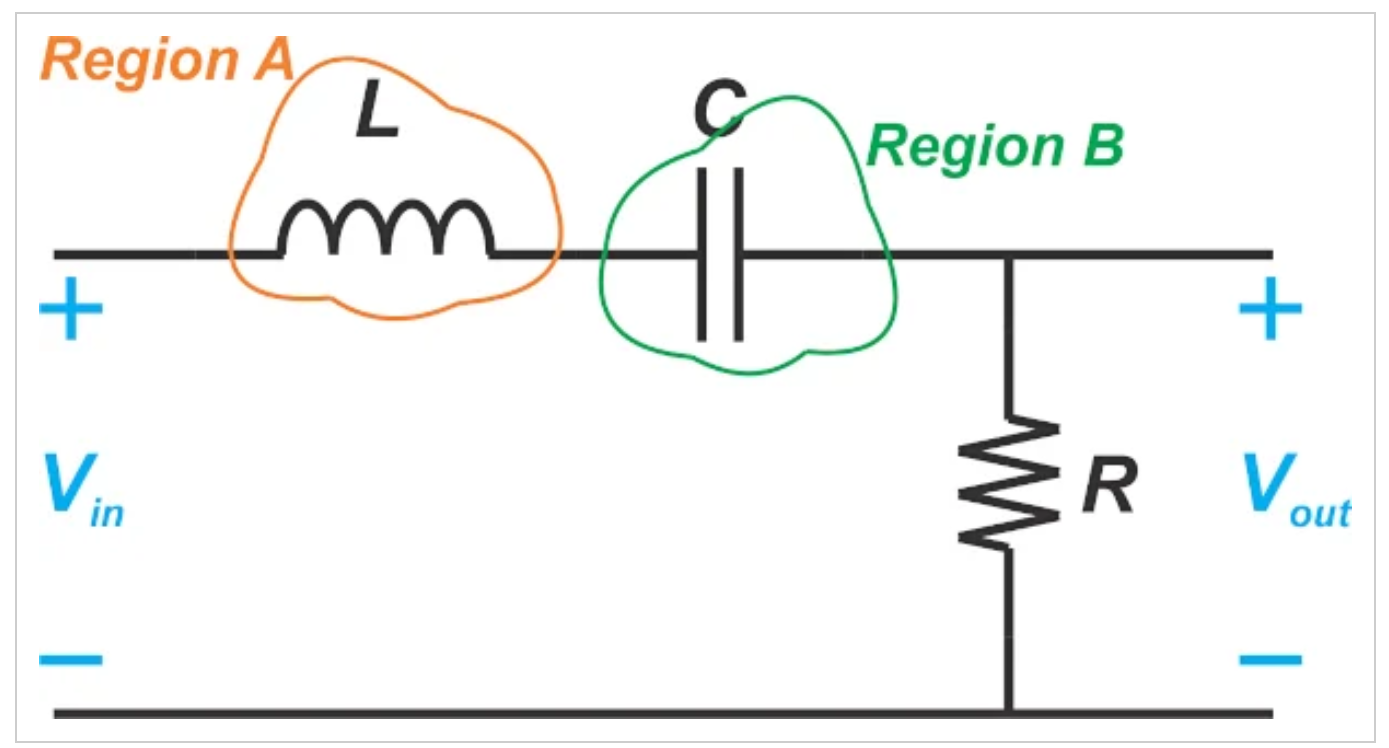
图1 无源带通滤波器的示例图
在上图中的“区域A”中,磁性储能占主导地位,因此,电路的这一部分表现为电感性。另一方面,在“区域B”中,电能存储在电场中,这意味着这部分被建模为电容器。在这个例子中,一些集总电容器、电感器等可用于模拟电路行为。我们在大学第一学期教授的电路理论和分析实际上是集总元件电路分析。对于集总电路,可以很容易地应用基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)来计算电路中的电压和电流。
相比之下,在分布式系统中,我们无法识别单独的电容器和电感器。例如,分布式系统中的均匀无损导线被建模为LC截面的无限梯形网络(图2)。

图2 LC段的无限梯形网络
该模型表明,每根无限短的电线都以磁场和电场的形式储存能量。这两种形式的能量存储分布在整个电线中。在这种情况下,我们无法将电路的电容性和电感性部分分开;它们混合在一起。
此外,在分布式系统中,电信号沿着电线以波的形式传播,这意味着电压和电流是沿着电线的时间和位置的函数。因此,我们可以说KVL和KCL在高频下不成立。
在下一节中,我将尝试以一种相对接近的方式推导相位常数方程。如果你对学习导数不感兴趣,你可以跳过下一节,从“方程式摘要”部分继续。
推导相位常数方程
无损传输线可以用两个重要参数来表征:特性阻抗Z0和相位常数β。特性阻抗指定了无限长线路的电压波与电流波的比率。相位常数表征了波如何随位置变化。对于无损线,Z0由方程1给出:
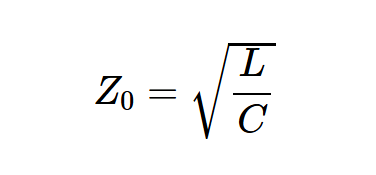
方程式1
为了推导β的方程,我们需要找到图3中梯形网络模型中出现的稳态电压和电流信号。

图3 梯形网络模型
根据第一LC部分的电压和电流参数,基尔霍夫电压定律得出:
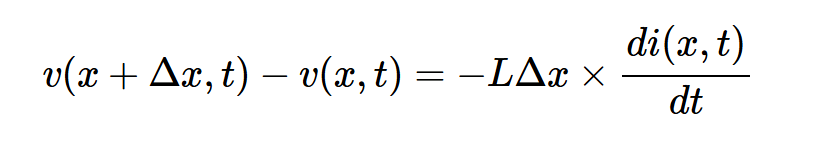
将两边除以Δx,我们得到:
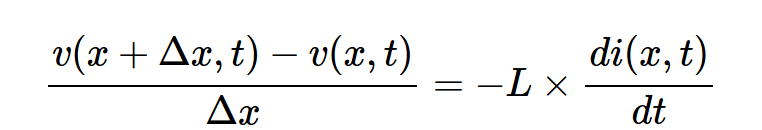
如果我们考虑当Δx接近零时该方程的极限,则左侧的表达式实际上变为v(x,t)相对于x的导数。因此,上述方程可以改写为方程2:
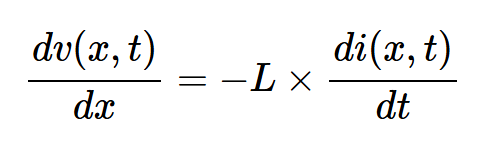
方程式2
对于一条无限长的线,沿线任何一点的电压与电流之比等于Z0。从方程式1中,我们得到:
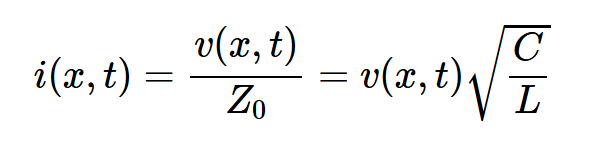
通过替换方程2中的i(x,t),得到方程3:
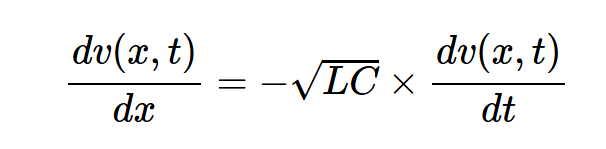
方程式3
现在,两侧都是线电压,但左侧是v(x,t)相对于位置的导数,而右侧包括函数相对于时间的导数。由于我们想要正弦激励的稳态响应(如vs(t)=Acos(ωt)),我们可以使用电路理论中的相量概念。
对于这种分析,我们可以假设输入是复指数电压Aejωt,而不是vs(t)=Acos(ωt),然后我们找到感兴趣的电压或电流信号。最后,我们取所获得信号的实部,以找到实际输入vs(t)=Acos(ωt)产生的输出。
当我们将Aejωt应用于电路时,ejωt项出现在所有电压和电流量中。例如,v(x,t)可被视为v(x)ejωt,其中v(x)是一个复数值,称为v(x,t)的相量。在基本电路理论中,相量显然不依赖于位置,因为我们处理的是集总电路。然而,在输电线路分析中,我们预计相量是位置的函数。将v(x,t)代入v(x)ejωt,方程式3得出:
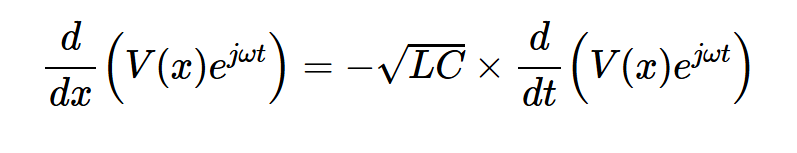
V(x)不是时间的函数,ejωt也不是x的函数。因此,使用一点代数,上述方程简化为:
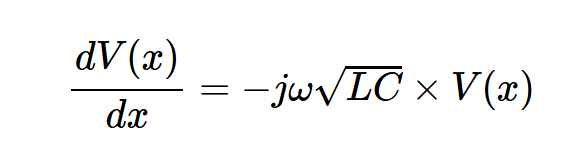
EE应该熟悉这个一阶微分方程的解:
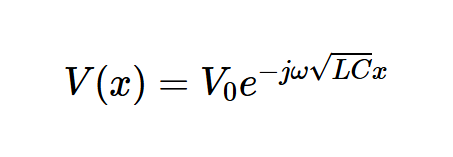
其中V0是一个常数,可以从线路输入和输出端口的边界条件中找到。从相量分析中,我们知道V(x)ejωt的实部是如果我们将vs(t)=Acos(ωt)应用于输入时得到的输出。因此,我们的最终电压波为:
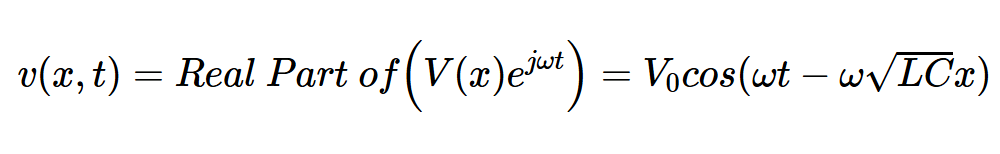
定义相位常数
β=ω√LC
,我们得到:
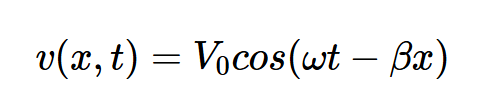
方程式4
这与我们在上一篇文章中讨论电压波如何沿传输线传播时使用的波函数相同。将方程4除以Z0得到正向电流波,如方程5所示:
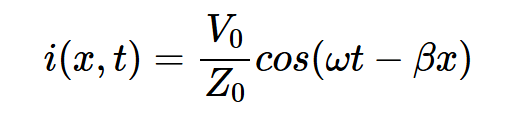
方程式5
无损过渡线方程概述
在上一节中,我们推导了正向电压和电流波的方程。一般来说,正向波和反射波都可以同时出现在线路上。对于无损线路,整体电压和电流波的形式如下:
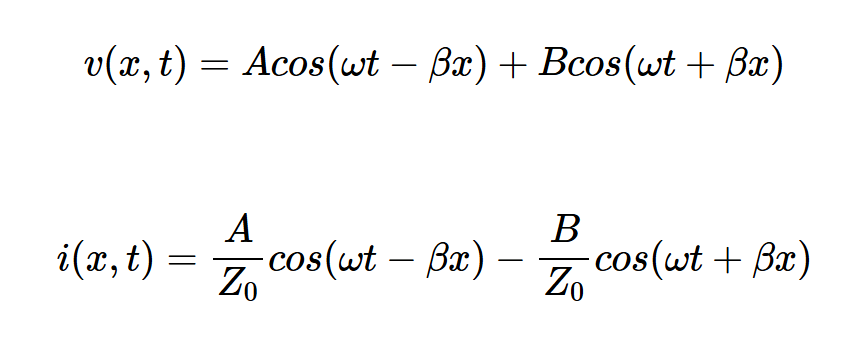
其中特性阻抗Z0和相位常数β为:
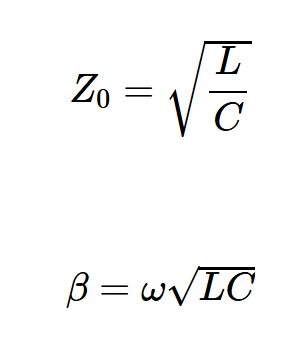
输电线路的分布式效应:是期望的还是麻烦的?
由于高频电信号的波动行为,射频设计人员痴迷于将负载阻抗与线路的特性阻抗相匹配。如果没有阻抗匹配,最大功率就无法传输到负载,驻波产生的大峰值电压会损坏电路组件或互连。然而,传输线的分布行为导致了一个非常有趣的特性。
基于上述分析,如果我们以任意频率ω1的正弦vs(t)=Acos(ω1t)激励线路,则正向电压波为:
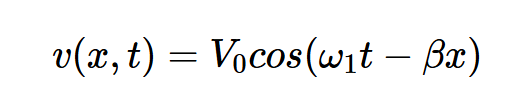
替换β,我们得到:
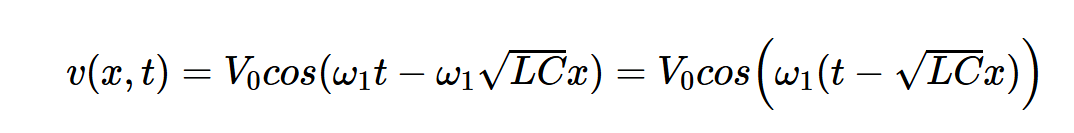
我们在给定位置x获得的信号与输入相同,除了它延迟了
.
此结果对任何频率都有效。唯一的假设是该线路是无损的,并且充当传输线。如果延迟与频率有关,则输入的不同频率分量将经历不同量的延迟,从而导致输出失真。例如,如果我们向具有频率相关延迟的系统施加脉冲,输出可能会完全失真,因为不同的频率分量以不相等的时间偏移到达输出。
如方程式所示,无损传输线以相同的延迟通过所有频率分量。换句话说,该线路具有无限带宽。如果我们增加L和C,延迟也会增加,但所有频率分量的延迟仍然是恒定的。如果你将其与我们对集总低频电路的直觉进行比较,你会发现这个功能更令人惊讶,因为增加电容值通常会降低系统带宽。
除了均匀延迟外,我们还应该有一个与频率无关的衰减,以使系统具有无限带宽。在上述讨论中,我们假设线路是无损的,因此,所有频率的衰减都是零。
有损的输电线路呢?
在现实世界的传输线中,损耗可能由许多因素造成,如导体损耗(趋肤效应)、介电损耗和磁滞效应。这些损失也与频率有关。然而,即使使用有损传输线,也可以调整线路参数以具有均匀的衰减和群延迟(至少在原则上)。要了解更多信息,您可以参考Thomas H.Lee的《CMOS射频集成电路的设计》一书。
高阶模式传播
除了损耗分量外,还有另一个因素限制了传输线的可用带宽。随着频率越来越高,信号的波长最终变得与传输线的横截面尺寸相当。在这种情况下,会产生与我们通常预期不同的电磁场配置。这些模式被称为高阶传播模式。高阶模的传播速度不同于主模的传播速率。因此,我们通常试图在传输线的第一高阶模式以下操作传输线。例如,根据导体的尺寸和所采用的电介质类型,可以指定同轴线工作高达约18GHz,以避免高阶模的传播。



评论