E类功率放大器设计方程的解

在这篇文章中，我们分析了E类放大器的操作，并检查了其设计方程的基本假设。

E类操作模式允许我们构建高效功率放大器，其输出功率水平从几千瓦（在低射频频率下）到大约一瓦（在微波频率下）不等。设计简单是E类放大器的主要优点之一——与其他放大器类别不同，它在初始设计阶段后需要最小的调整才能达到令人满意的性能。

对E类运算的全面分析需要一些相当冗长乏味的数学。相反，本文将使用简化的假设来创建分析的简化版本，并推导出E类功率放大器的基本设计方程。尽管我们在上一篇文章中介绍了这些方程中的大部分，但这里包含的蒸馏分析应该可以帮助您自信地将它们应用于您的应用程序。

完成电路分析后，我们将检查我们的初始假设如何影响结果。本节还将为那些想要更深入治疗的人提供参考文献和阅读建议列表。

图1显示了我们将要研究的基本E类阶段。其典型的开关波形如图2所示。

基本E类放大器示意图。

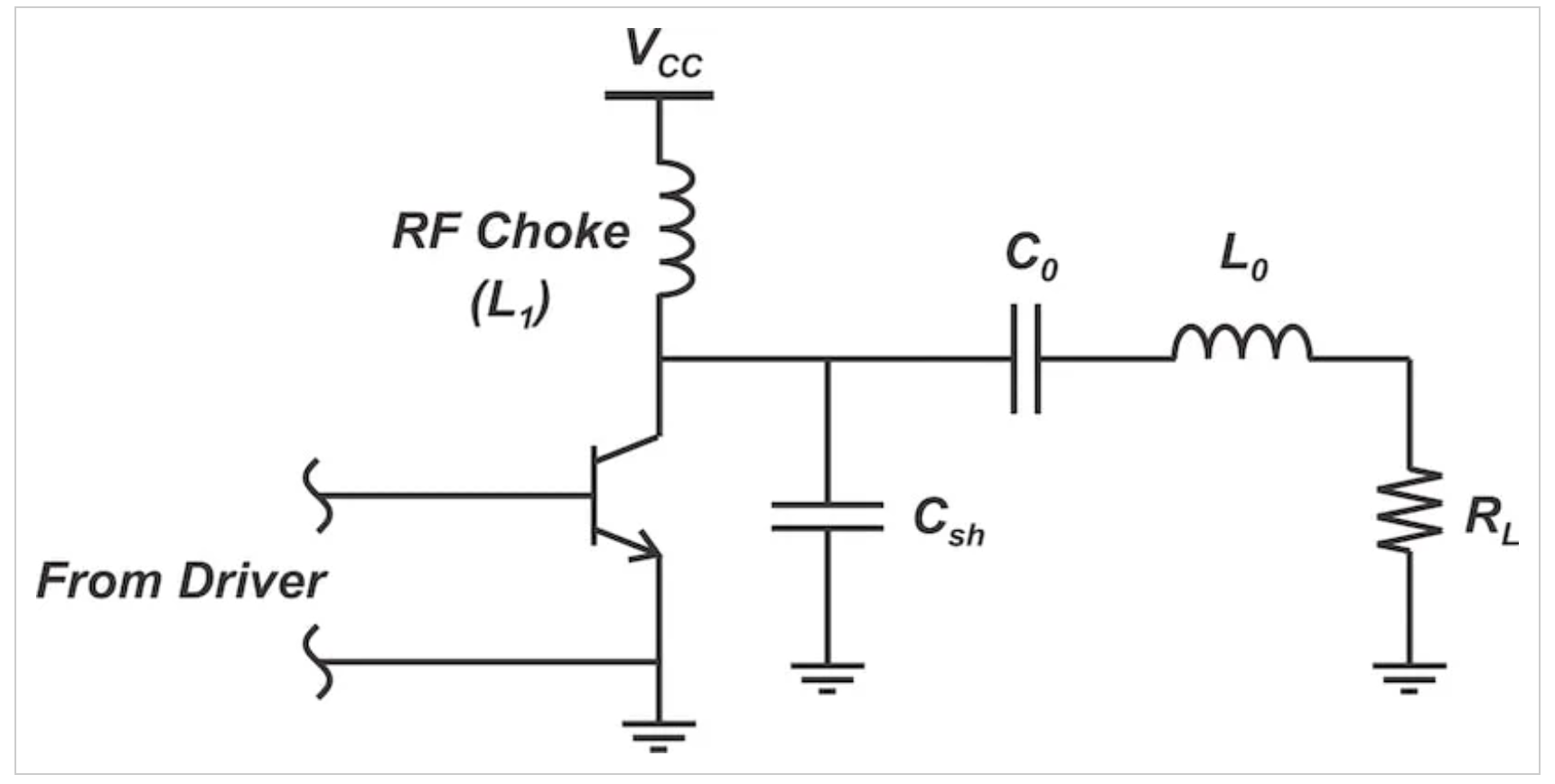
图1 基本E类放大器示意图

E类放大器的典型开关电流和开关电压波形。

图2 E类放大器中典型的开关电流（顶部）和开关电压（底部）波形

您可能已经熟悉本系列早期文章中的这些数字。为了方便起见，这里转载了它们，因为我们将在整个讨论过程中引用它们。

至此，让我们开始分析。

求并联电容器两端的电压

假设负载网络的Q值足够高，E类放大器的输出电流在开关频率下为正弦曲线。负载电流由下式给出：

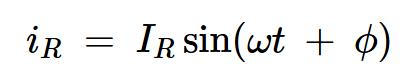
方程式1

其中IR是电流的峰值，ϕ是其初始相位。

RF扼流圈为电源提供直流路径，并在RF处近似开路。在图3中，通过射频扼流圈的直流电流用I0表示。

RF扼流圈提供I0的直流电流，正弦电流iR流过负载。

图3 RF扼流圈提供I0的直流电流，正弦电流iR流过负载

在上图中，流过开关和并联电容器的总电流为：

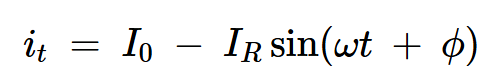
方程式2

因此，流过开关和电容器的电流是一个偏移正弦波。

假设在时间间隔0<⍵t<π内，开关处于ON状态。在此间隔内，它完全通过开关。假设开关的饱和电压可以忽略不计，则集电极电压处于地电位。

在下一个半周期（π<⍵t<2π），开关断开，它完全流过电容器。当开关断开时，分流电容器两端的电压（vc）可以通过在相关时间间隔内对其进行积分来计算：

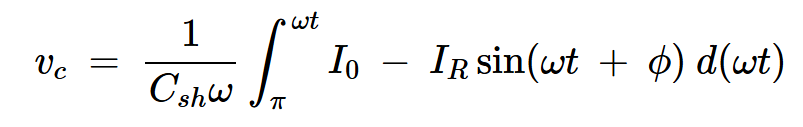
方程式3

这导致：

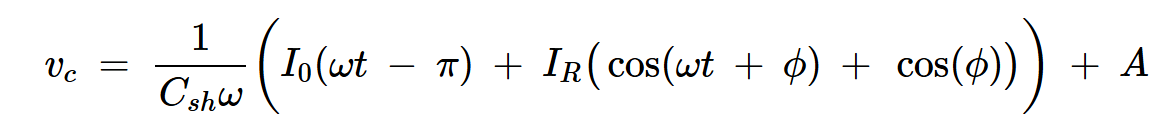
方程式4

其中A是积分常数。

在我们继续之前，请注意，在开关打开的瞬间，开关电流被转移到分流电容器。这是理想E级操作的一个决定性方面。

应用零值和零导数条件

在时间间隔0<⍵t<π期间，开关处于ON状态，集电极电压处于地电位。就在⍵t=π之后，并联电容器两端的电压为零。将此条件应用于方程式4，得出A=0。

在E级阶段，当开关接通时，开关/电容器两端的电压也为零。因此，vc在⍵t=2π时必须为零（见图2）。从方程式4中，我们得到：

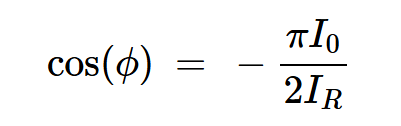
方程式5

此外，在理想的E类阶段，开关/电容器电压的斜率在开关接通的瞬间为零。取方程4关于⍵t的导数，并将其在90.77; t=2π处等于零，我们得到：

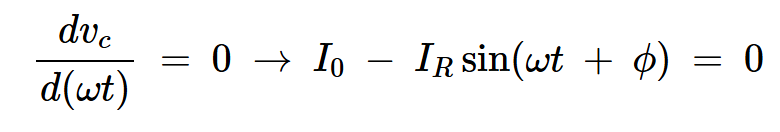
方程式6

这在电路参数之间产生了另一种有用的关系：

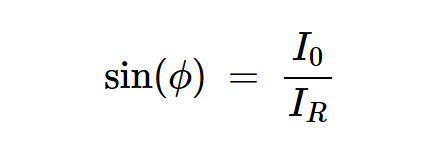
方程式7

最后，我们结合方程5和7，使用切线方程来确定电流的初始相位：

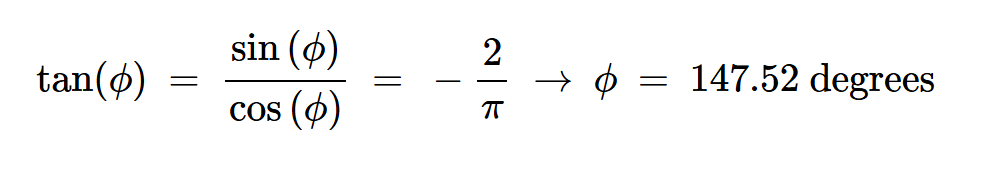
方程式8

实现100%效率

使用理想的组件，E类放大器的效率为100%。这是因为开关电压和电流波形不重叠，将开关功率损耗降至零。这意味着电源提供的所有直流电都被输送到负载：

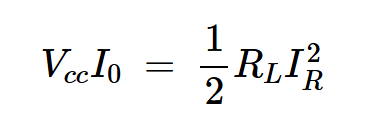
方程式9

将该方程与方程7相结合，我们得到负载电流：

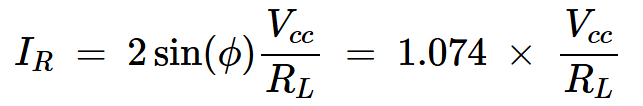
方程式10

以及流过RF扼流圈的DC电流：

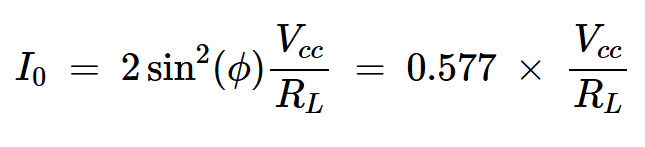
方程式11

求并联电容和负载网络电感

到目前为止，我们已经计算了负载电流的初始相位（ϕ=147.52度），并找到了将I0和IR与电源电压和负载电阻相关的表达式。接下来，让我们找到所需的分流电容（Csh）。

我们有几种不同的方法可以做到这一点。在一种方法中，我们首先注意到理想射频扼流圈两端电压的直流分量为零。因此，开关和并联电容器两端的电压直流值必须等于电源电压：

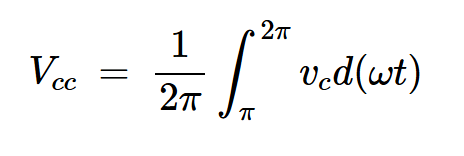
方程式12

从方程4中替换vc并使用一些代数得到：

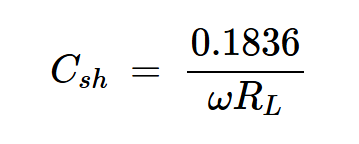
方程式13

另一种方法涉及识别开关/电容器电压的基本分量。我发现这种方法更具吸引力，因为它不仅可以确定Csh，还可以确定图1中电路的其他组件，即L0和C0。为了理解这种方法，我们需要在基频下检查负载网络（图4）。

基频下的负载网络模型。

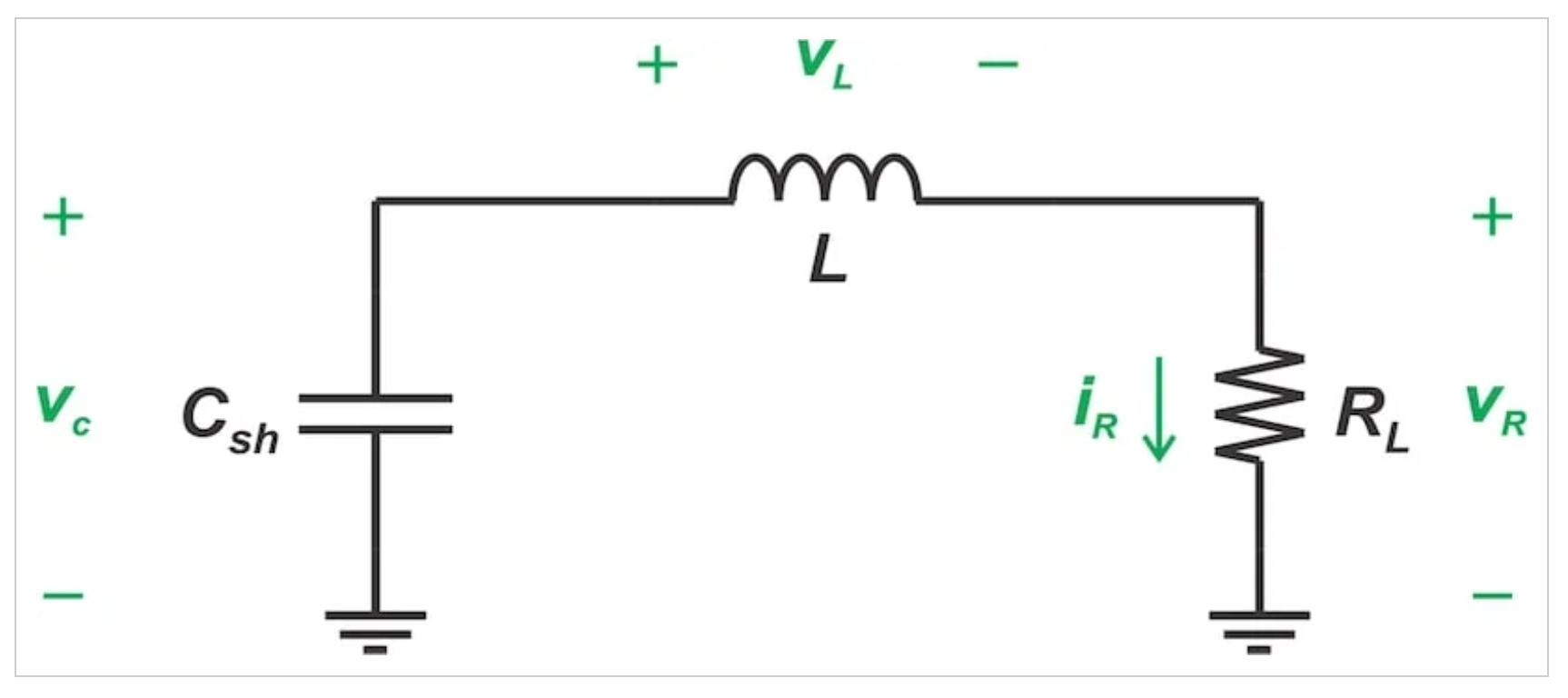
图4 基频下E类放大器负载网络的模型

在上图中，L是串联谐振电路在基频下呈现的有效电感。L不应与L0混淆，它包括L0和C0的影响。正如我们在上一篇文章中讨论的那样，E类放大器在工作频率下的负载电抗为非零，其值与负载电阻（RL）相当。我们研究过的其他射频放大器类通常使用调谐到工作频率的谐振电路，使其在基频下具有零负载电抗。

让我们回到图4中分析网络。我们目前的目标是确定Csh和L在RL方面的值。我们知道，流经网络的电流是一个正弦曲线，振幅为IR，初始相位为ϕ，分流电容器两端的电压由方程4给出。

我们可以使用频域或时域方法来解决这个问题。我将使用时域方法，因为我觉得它更直观。计算RL两端的电压轻而易举：

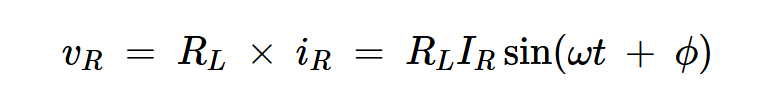
方程式14

理想电感器两端的电压使其电流恰好领先90度。由于电流表示为正弦函数，电感器两端的电压是时间的余弦函数：

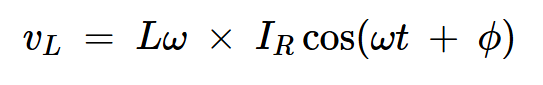
方程式15

因此，在基频下分流电容器两端的电压为：

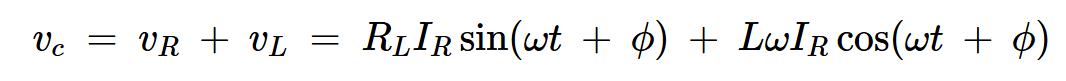
方程式16

这意味着分流电容器两端的电压由两个分量组成：

与输出电流同相的组件。

作为时间余弦函数的分量（正交分量）。

通过应用傅里叶分析，我们可以找到这两个分量。同相分量（vci）计算如下：

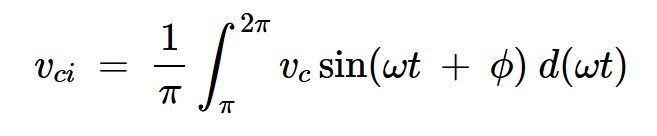
方程式17

类似地，正交分量（vcq）由下式给出：

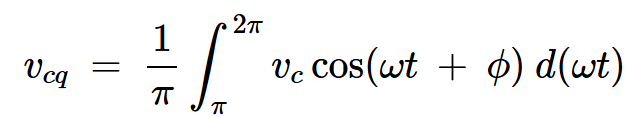
方程式18

通过执行一些基本的（如果有点长）计算，我们可以简化方程17和18，得到以下结果：

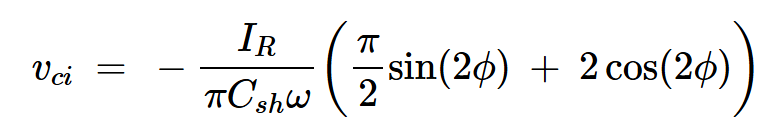
方程式19

以及：

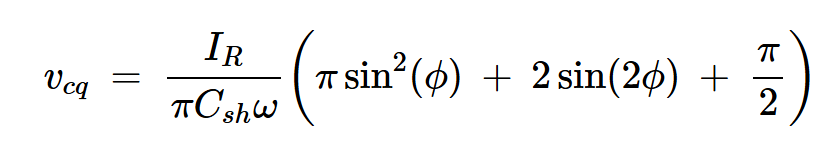
方程式20

根据方程式16，同相和正交分量的峰值分别为RLIR和L⍵IR。将vci设置为RLIR并使用ϕ=147.52度会导致：

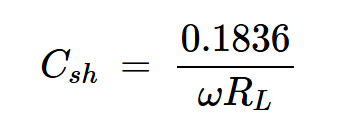
方程式21

这与方程式13相同。

最后，将vcq与L⍵IR相等，并使用ϕ=147.52度，我们得到：

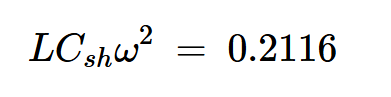
方程式22

查找L0和C0

现在我们可以找到L0和C0，串联谐振电路的组件。在给定负载网络的Q值的情况下，我们可以使用以下方程来确定L0的值：

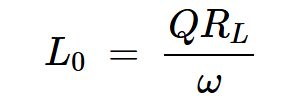
方程式23

基频下的有效电感电抗为：

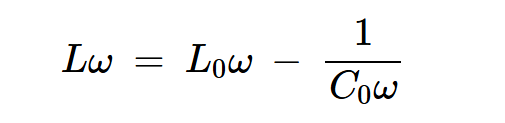
方程式24

其中L和L0分别由方程22和23给出。方程式24有时也写为：

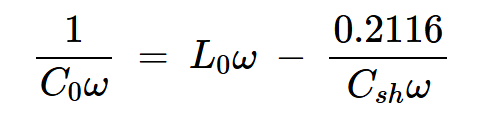
方程式25

检查我们的假设

现在我们已经推导出了设计方程，是时候考虑我们在上述分析中做出的假设了：

Q值足够高，可以产生正弦输出电流。

50%的占空比。

具有零导通电阻、无限截止电阻和瞬时切换时间的开关。

无损无源元件，包括理想的射频扼流圈。

让我们更仔细地研究一下这些。

高Q值和正弦输出电流

在整个分析过程中，我们假设输出电流在开关频率下是正弦曲线。从技术上讲，这将要求负载网络的品质因数（Q）无限高。Q的实际值在3到10之间，允许一些谐波电流流入负载网络。Q越低，我们对输出电流的假设就越不准确。

如果我们在Q值不够高的设计中使用导出的方程，我们可能无法实现最佳操作所需的零电压和导数开关条件。有关不假设高Q值的全面分析，请参阅M.Kazimierczuk的“在任何Q值和开关占空比下对E类调谐功率放大器的精确分析”。

 50%的占空比

尽管我们假设占空比为50%，但这并不是E类操作的基本要求。然而，分析电路的任意占空比值更为复杂。

对于那些感兴趣的人来说，可以在F.Raab的经典论文《E类调谐功率放大器的理想化操作》中找到对任何占空比值的分析。Steve Cripps博士的《无线通信射频功率放大器》一书也分析了E类放大器的任意占空比，这本书对初学者来说可能更容易理解。

理想电路元件

我们假设我们的组件——开关、射频扼流圈、串联电感器和电容器——是理想的。然而，现实生活中的开关不会有零导通电阻、无限截止电阻或瞬时开关时间。我们还将看到由于电感器和电容器的等效串联电阻而导致的一些功率损失。由于这些非理想性，即使在满足零电压开关条件且导通开关损耗为零时，我们也需要在设计中考虑关断开关损耗。

最后，我们假设只有直流电流流过射频扼流圈。这将需要一个具有无限电抗的扼流圈，这在实践中是不可行的。

总结

在本文中，我们对E类放大器进行了简化分析。如果你有兴趣更深入地探讨这个话题，我在下面列出了参考文献：

M.K.Kazimierczuk的“射频功率放大器”。

A.Grebennikov、N.O.Sokal和M.J.Franco的“开关模式射频和微波功率放大器”。

J.B.Hagen的“射频电子电路和应用”。

在下一篇文章中，我们将探讨实际的Q值（通常在3到10之间）如何导致谐波电流流入负载。然后我们将讨论如何解决这个问题。