共漏极放大器介绍:小信号行为
共漏极放大器是一种单级配置,它使用栅极作为其输入,源极作为其输出。本文将介绍其小信号特性。
共漏极放大器有时也称为源极跟随器,由于其低输出阻抗和高输入阻抗,在CMOS设计中非常有用。本系列的前一篇文章讨论了源极跟随器的大信号工作原理。在本文中,我们将分析以下小信号特性:
信号增益小。
输出电阻。
频率响应。
图1显示了我们将要检查的电路。为了简单起见,它与我们在上一篇文章开头介绍的电路相同。这是共漏极放大器的最基本版本;与现实世界的实现不同,它使用理想的电流源。
前一篇文章中的基本共漏极放大器。
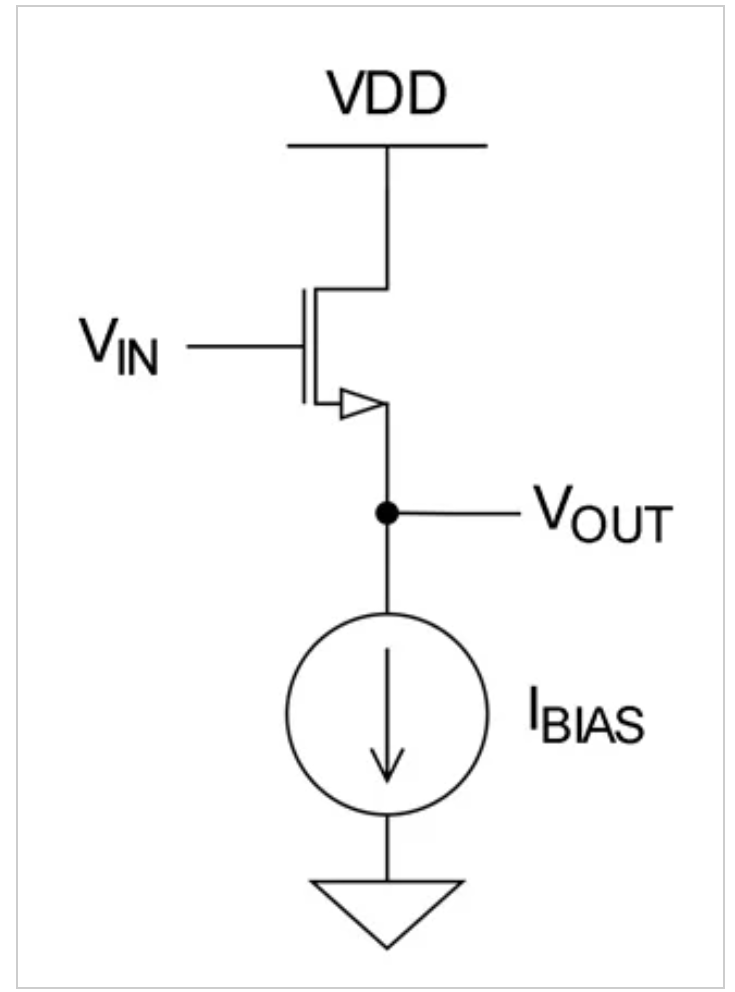
图1 基本共漏极放大器配置。
漏极连接到VDD,因为放大器使用NMOS晶体管。如果晶体管是PMOS,则漏极将连接到地。
小信号增益
上述电路的小信号模型如图2所示。让我们用它来求解传递函数。
图1中共漏极放大器的小信号模型。
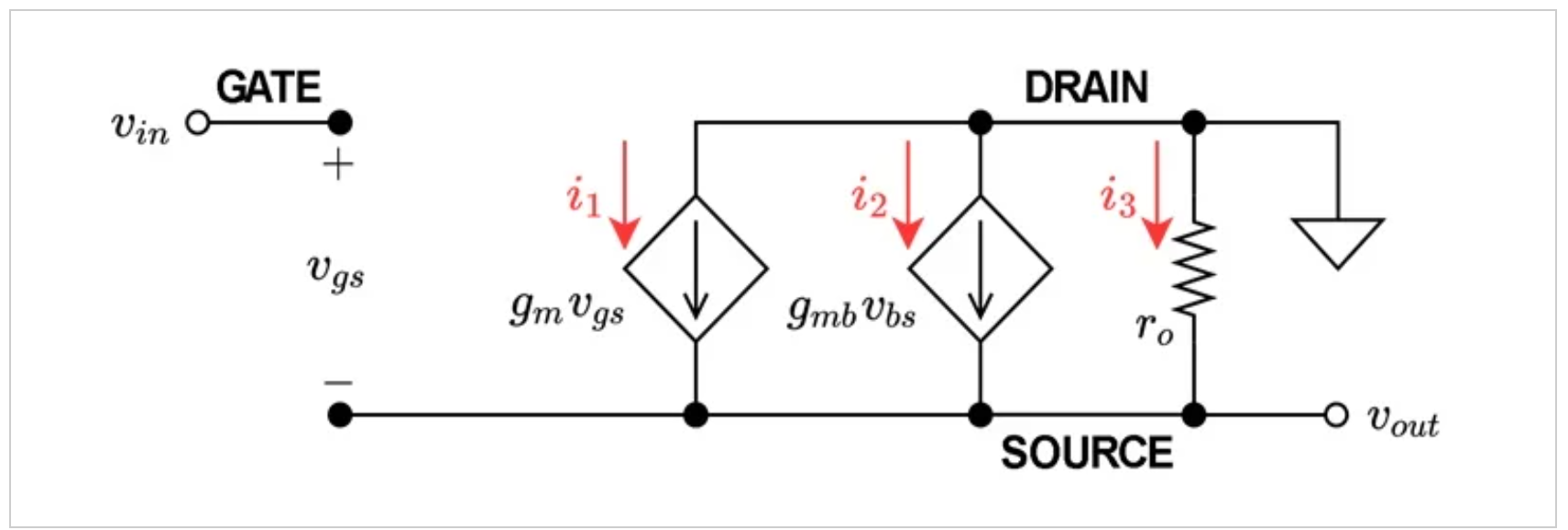
图2:图1中共漏极放大器的小信号模型。
根据基尔霍夫电流定律,输出节点处所有电流的总和等于零。对于图2,这意味着:
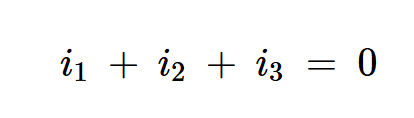
方程式1。
在这个模型中,vgs = vin – vout and vbs = –vout。记住这一点,我们可以从图2中得出i1、i2和i3的值:
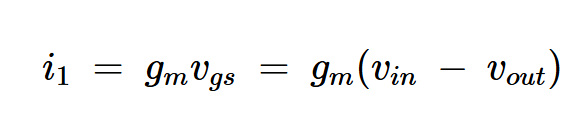
方程式2。
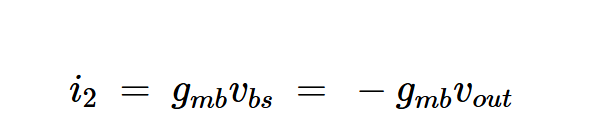
方程式3。
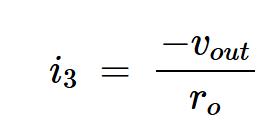
方程式4。
解释:
ro是晶体管的输出电阻
gm是跨导
gmb是体效应跨导。
因为共漏极放大器的源极不接地,所以体效应始终存在。将这些电流值代入方程1,我们得到:
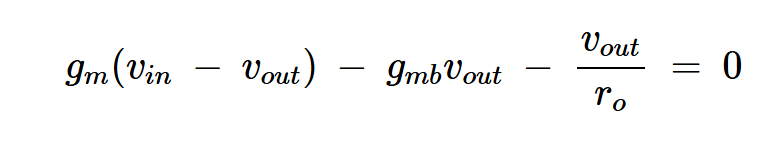
方程式5。
收集术语的结果如下:
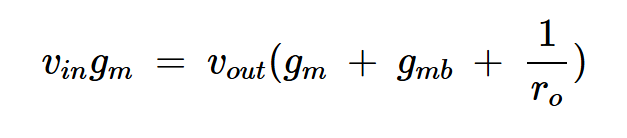
方程式6。
使用方程式6和增益公式 Av = voutvin Av = voutvin
我们现在可以求解小信号增益:
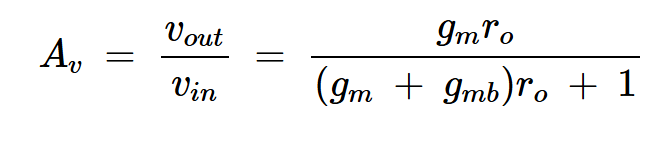
方程式7。
由此,我们确认了在大信号分析中看到的情况——源极跟随器充当电压缓冲器。尽管由于体效应,增益永远不会精确为1,但它可以非常接近1。
既然我们已经计算出了小信号增益,那么让我们来检查共漏极放大器的电阻。
输出电阻
由于放大器的输入端是晶体管的栅极,因此输入电阻为无穷大。本节将不再进一步考虑。为了找到输出电阻,我们将测试电压(vt)连接到输出节点,并在放大器输入接地的情况下计算从中流出的电流(it)。图3显示了我们的测试设置。
用于寻找共漏极放大器输出电阻的测试设置。
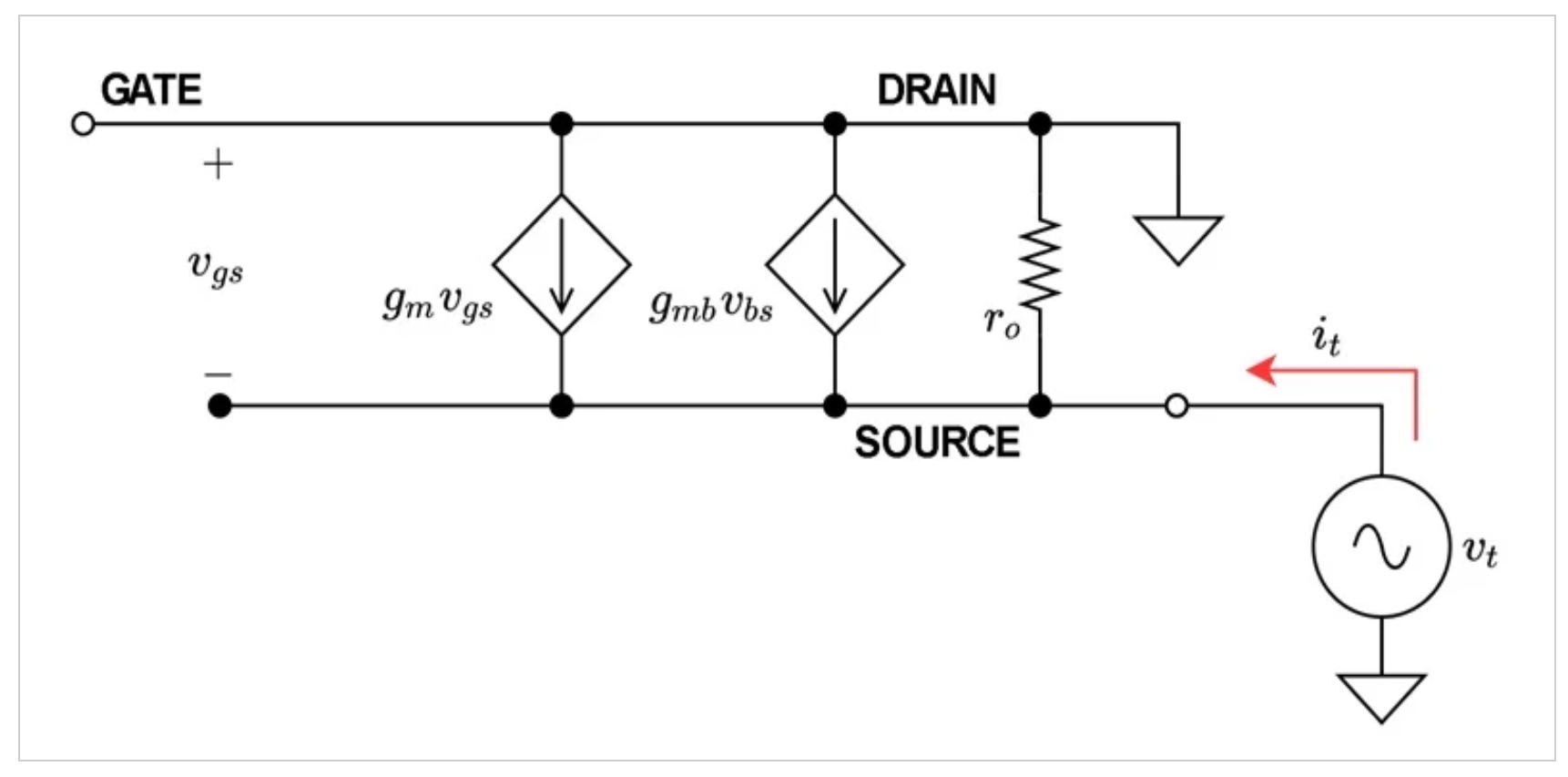
图3. 用于找到图1中共漏极放大器的输出电阻的测试设置。
根据此图,并认识到vgs = –vt和vbs = –vt,我们发现测试电流为:
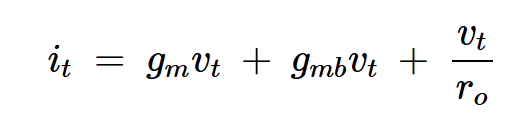
方程式8。
输出电阻等于测试电压除以测试电流(Rout = vtit)
因此我们有:
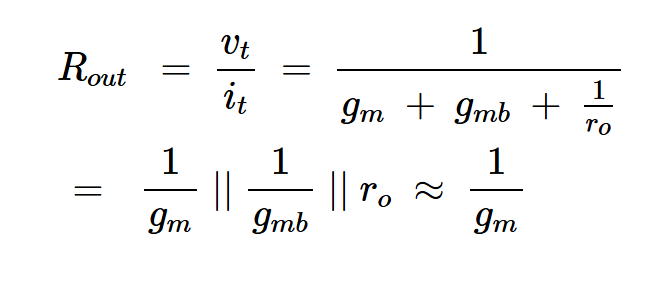
方程式9。
这些方程说明了源极跟随器的输出电阻非常低,具有吸引力。其近似值为 1gm1gm
比晶体管输出电阻(ro)小很多,这表明放大器能够将高阻抗增益级与其输出负载隔离开来。
频率响应
最后,让我们使用图4中的电路和小信号模型来研究共漏极放大器的频率响应。请注意,这次我们忽略了体效应和沟道长度调制。
共漏极放大器电路原理图和对应的小信号模型。
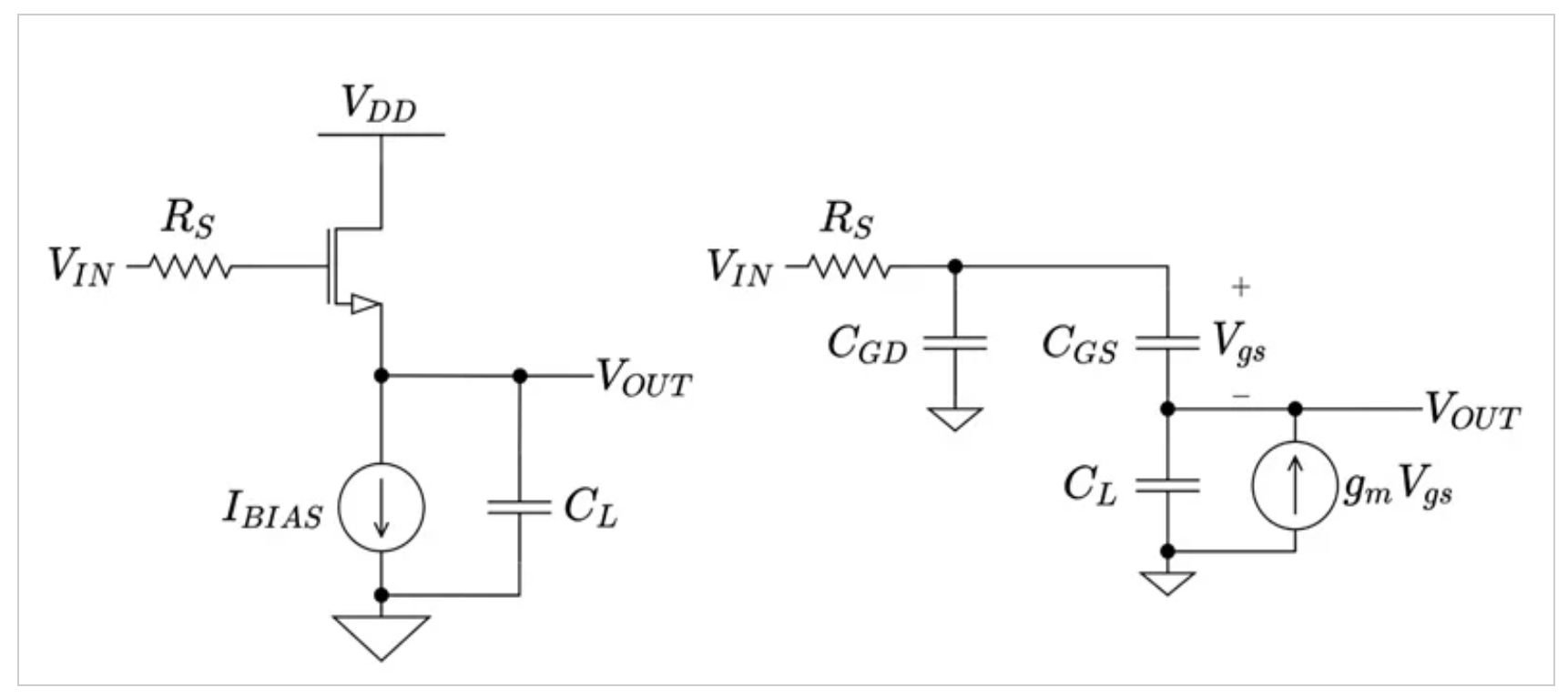
图4. 用于频率计算的共漏极放大器(左)和相应的小信号模型(右)。
如果我们计算上述小信号模型的传递函数,我们得到:
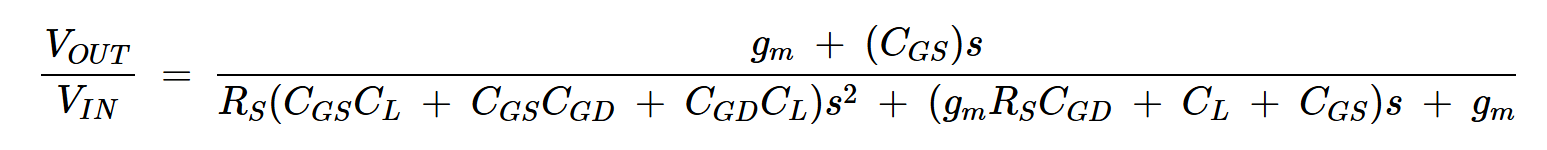
方程式10。
解释:
CGS是栅极到源极电容
CGD是栅极到漏极电容
CL是负载电容
RS是源电阻
s 是复数频率。
从等式10中可以看出,源极跟随器在左半平面有两个极点和一个零点。这是由于栅极到源极电容在高频下使输入和输出节点短路造成的。
输入和输出阻抗(分别为Zin和Zout)也可以告诉我们一些关于该放大器频率响应的有趣信息。为了计算Zin,我们将使用图5中的电路。
用于查找输入阻抗的源跟随器测试设置。
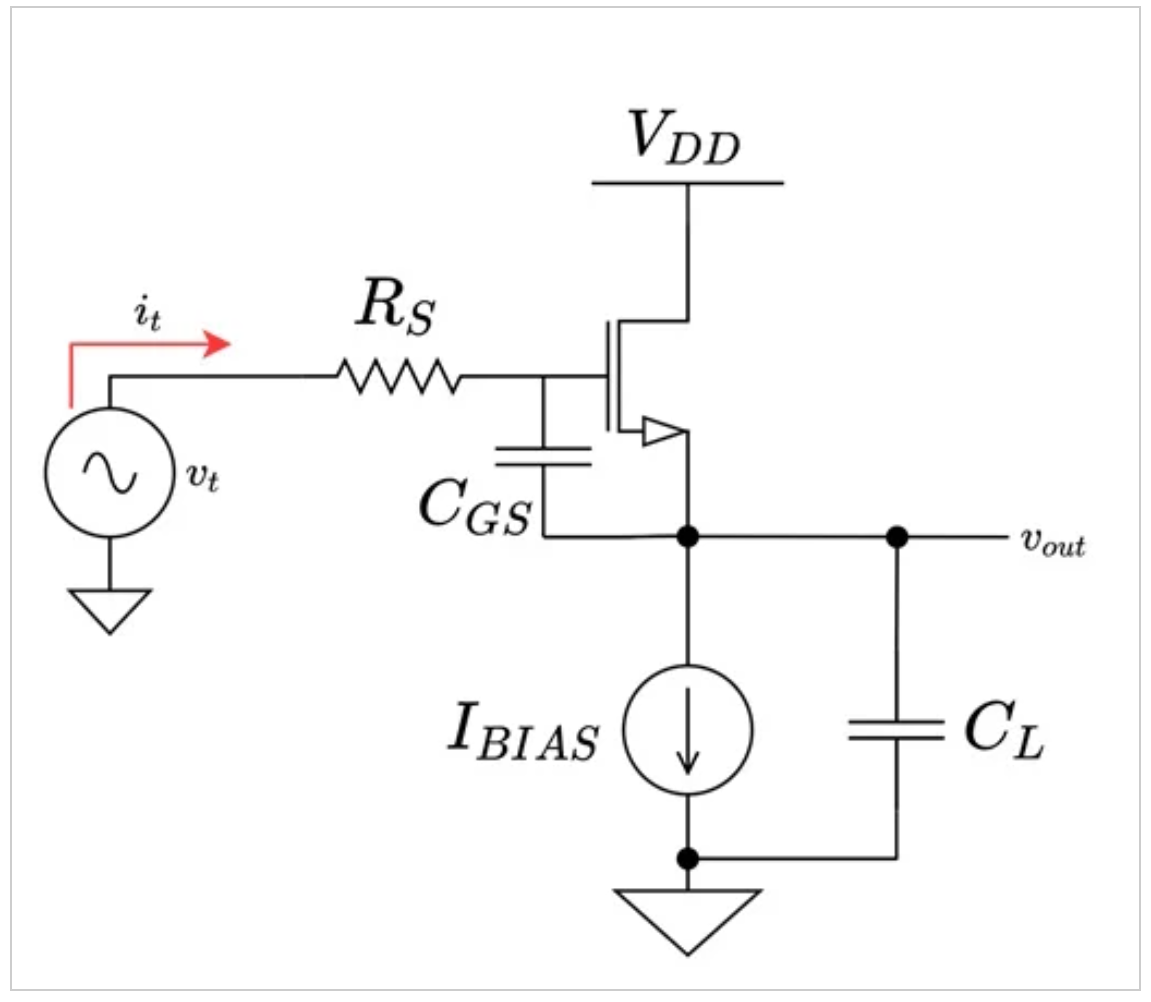
图5. 用于查找输入阻抗的源极跟随器测试设置。
如果我们忽略体效应,则输入阻抗为无穷大。如果我们不忽略体效应,则得到:
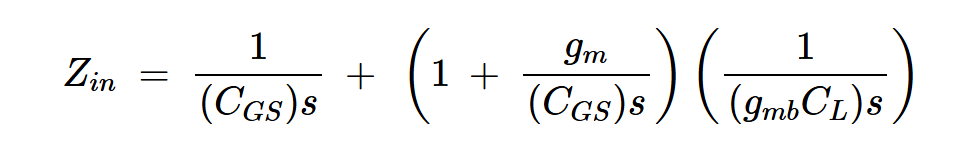
方程式11。
当最后两个项相乘时,分母中会出现s2。这意味着输入阻抗在某些频率下可能为负。负阻抗可能导致系统不稳定,使得源极跟随器在振荡器设计中非常有用。
为了找到Zout,我们在图4的输出端添加一个测试电压源,并测量其输出电流。当我们将测试电压除以输出电流时,我们得到:
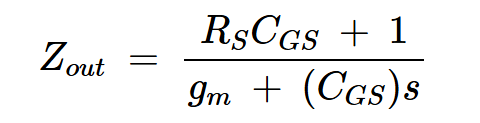
方程式12。
从这个方程中,我们可以观察到共漏极放大器的频率响应:
在低频时,Zout = 1/gm。
在高频时,Zout = RS。
如果RS > 1/gm,输出阻抗随频率增加而增加。
这种行为类似于电感器,使得源极跟随器在高频率应用中作为电感器的替代品具有重要价值。
总结
理解电路的小信号操作非常重要,特别是在设计模拟集成电路时。在小信号分析中,我们通过关注在定义的偏置条件下的操作来忽略晶体管的非线性、大信号行为。



评论