用最小二乘法解热电偶近似误差

了解k型热电偶的线性近似误差，以及如何使用最小二乘法和Matlab来找到最小化近似误差的最佳拟合线。

之前，我们研究了热电偶冷端补偿（CJC）的硬件实现。CJC电路需要感测冷端（Tc）的温度，并在Tc的温度下产生与热电偶产生的电压相等的补偿电压。

总的来说，热电偶是非线性的，由简单的模拟电路产生的补偿电压只能近似实际响应。因此，使用线性方程来近似热电偶响应会给我们的测量带来误差。

考虑到所有这些，本文将研究这个误差，并看看我们如何使用最小二乘法来找到最小化近似误差的最佳拟合线。

K型热电偶线性近似误差的评定

下图1显示了K型热电偶的输出和我们在上一篇文章中使用的线性近似值。

K型热电偶的输出和线性近似。

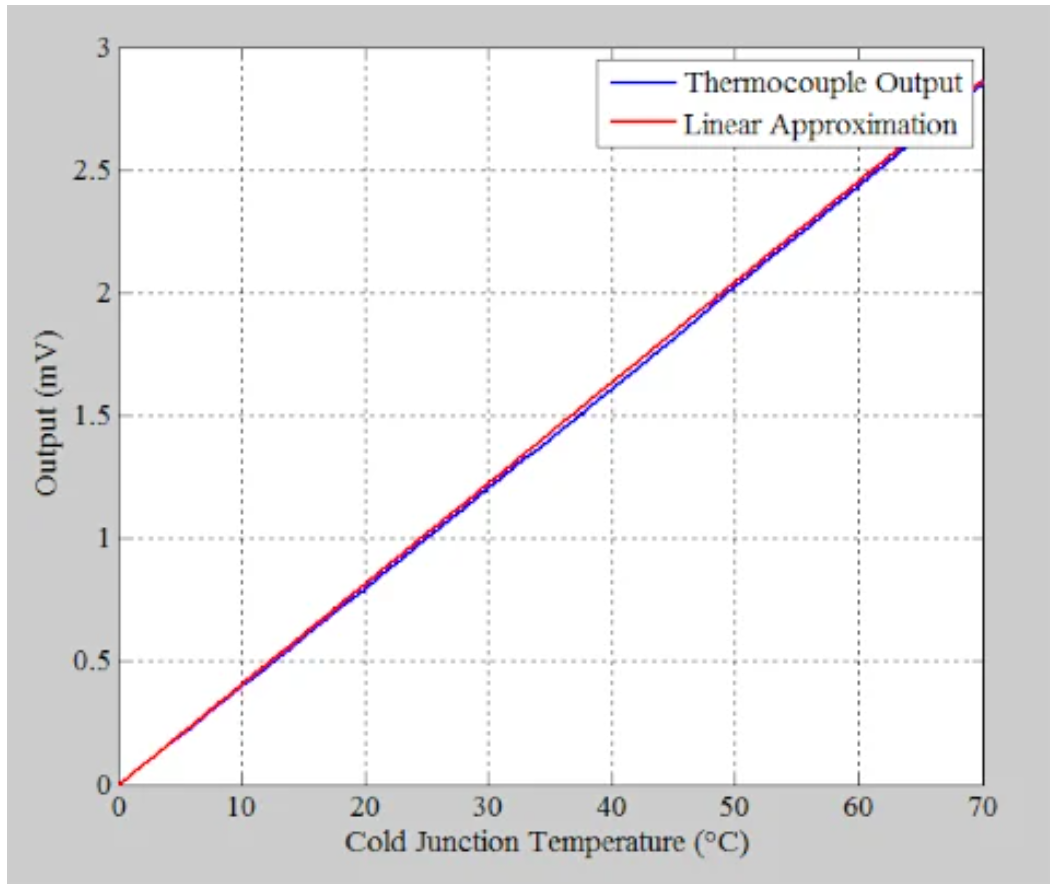
图1。K型热电偶的输出和线性近似。

在这种情况下，我们假设热电偶响应的斜率是恒定的，等于其在室温下的值（25°C时为41μV/°C）。如图所示，所采用的直线穿过原点。通过减去这两条曲线，我们得到了图2所示的μV近似误差。

以μV为单位的近似误差图。

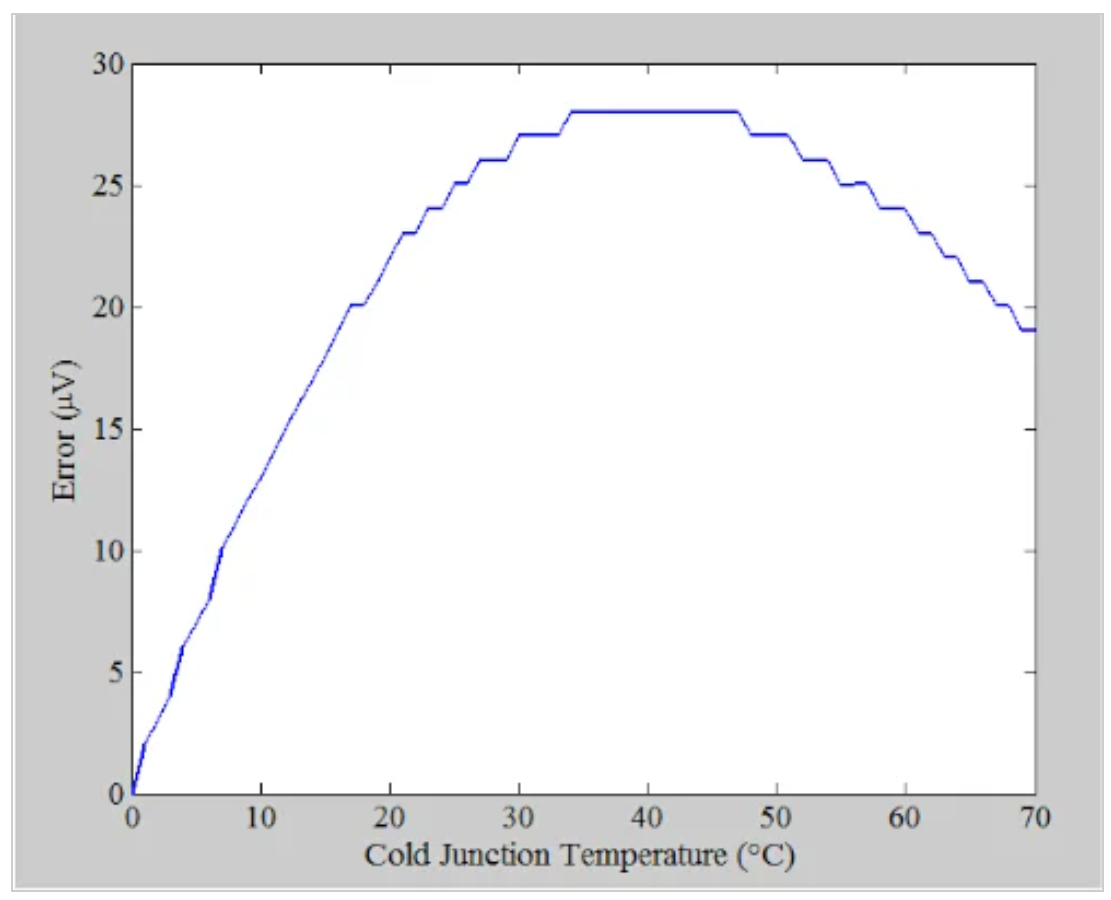
图2:以μV为单位的近似误差图。

接下来，通过将差分曲线除以直线的斜率（41μV/°C），我们得到了以°C为单位的误差，如图3所示。

显示误差与冷端温度的关系图。

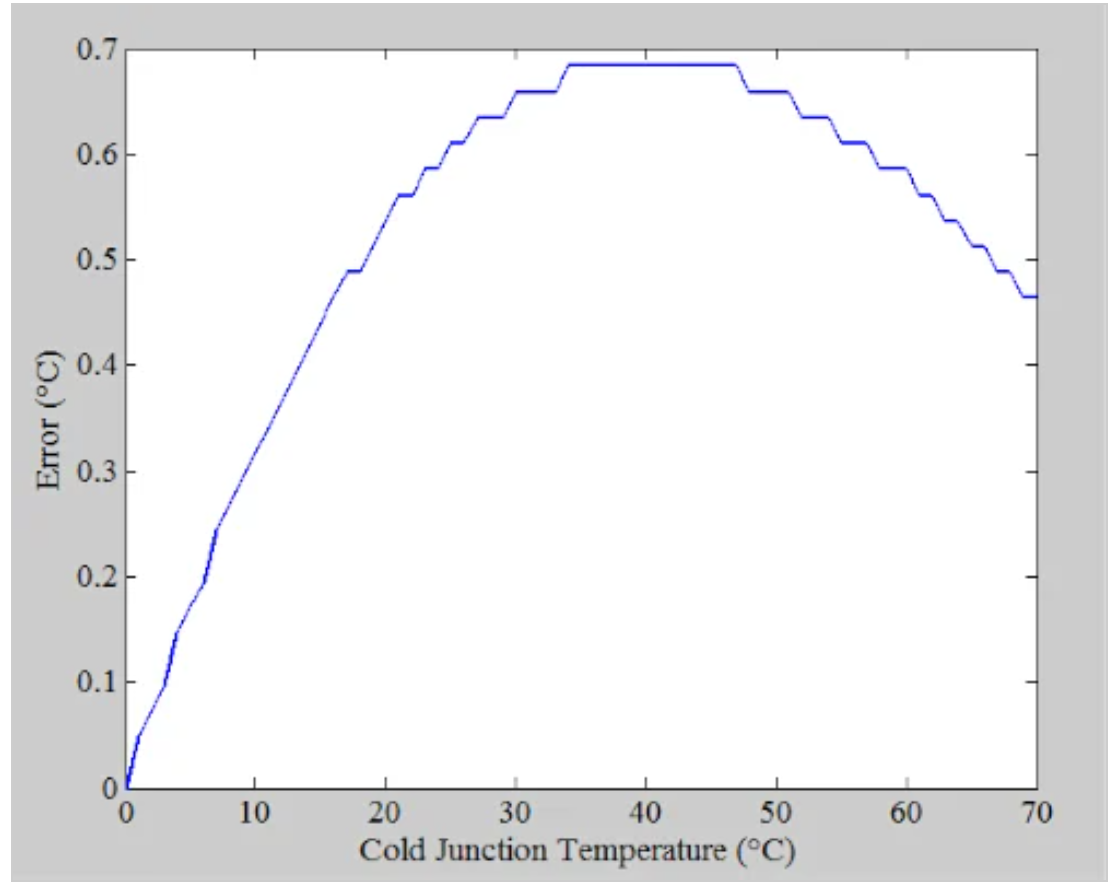
图3。显示误差与冷端温度的关系图。

上图显示，即使使用理想的电路元件，当Tc从0变化到70°C时，我们也会有大约0.7°C的误差。这个误差仅源于我们的线性近似。我们可以使用最小二乘回归线方法[视频]来找到最适合我们数据点的线性方程。

用最小二乘法寻找最佳拟合线

我们将通过一个例子解释最小二乘拟合过程。假设我们有以下数据点：

表1。示例数据点。

我们想找到最能代表这些数据点的直线。图4显示了这些点以及通过目视检查选择的直线，该直线试图遵循数据中的趋势。

显示示例数据点和线性近似值的图。

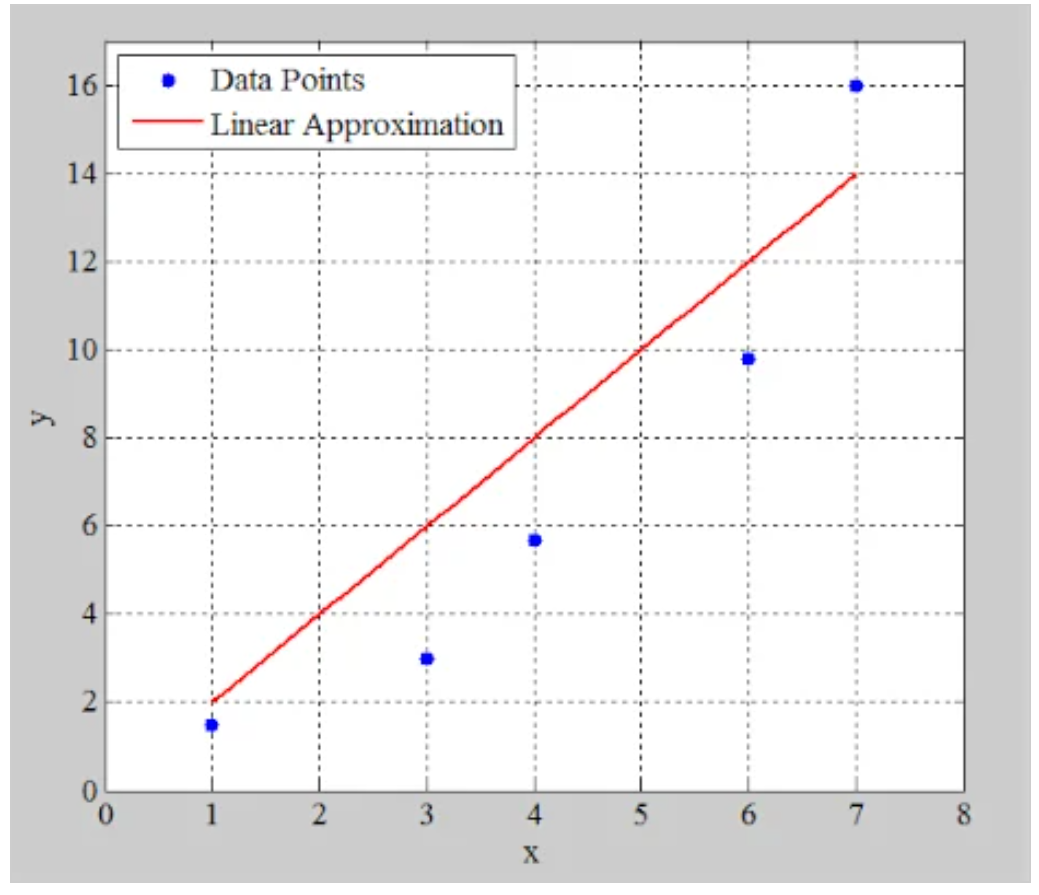
图4。显示示例数据点和线性近似值的图。

正如你所看到的，一条直线不能穿过所有这些点。因此，我们的线性近似可能会给出与数据点实际值不同的值。例如，在图4中，直线在x=7处给出y=14，而在该x值处实际值为16。因此，实际值与我们的线性模型产生的值之间存在2个单位的差异。

在最小二乘法的背景下，实际曲线值和线性模型值之间的差异称为残差（本文中用r表示）。在这个例子中，x=7处的残差等于r=+2。残差的平方和可以被视为我们的线性模型与数据拟合程度的指标。根据图4所示的模型，我们有：

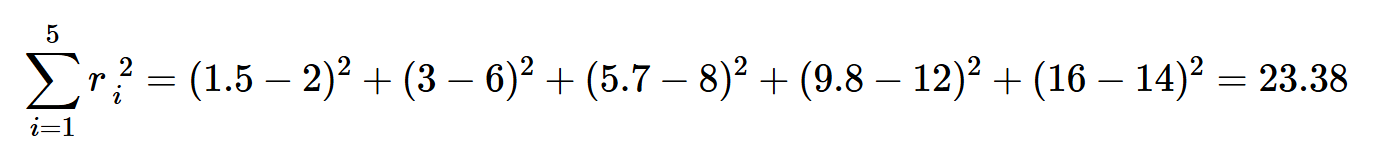
其中，总和指数（i）是指我们数据中的第i个点。最小二乘法试图通过调整线性模型的斜率（m）和y轴截距（b）来最小化所有数据点的残差平方和。使用下面的方程式1和2可以找到“最适合”数据的线性模型的斜率和y轴截距：

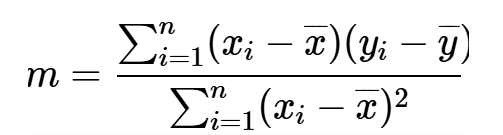
方程式1。

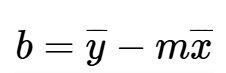
方程式2。

解释：

xi和yi是第i个数据点的x和y值

x和y是所有xi和易的平均值

n是数据点的总数

根据表1中给出的数据，我们得到x=4.2和y=7.2。表2显示了将方程1和2应用于我们的数据点时的一些计算。

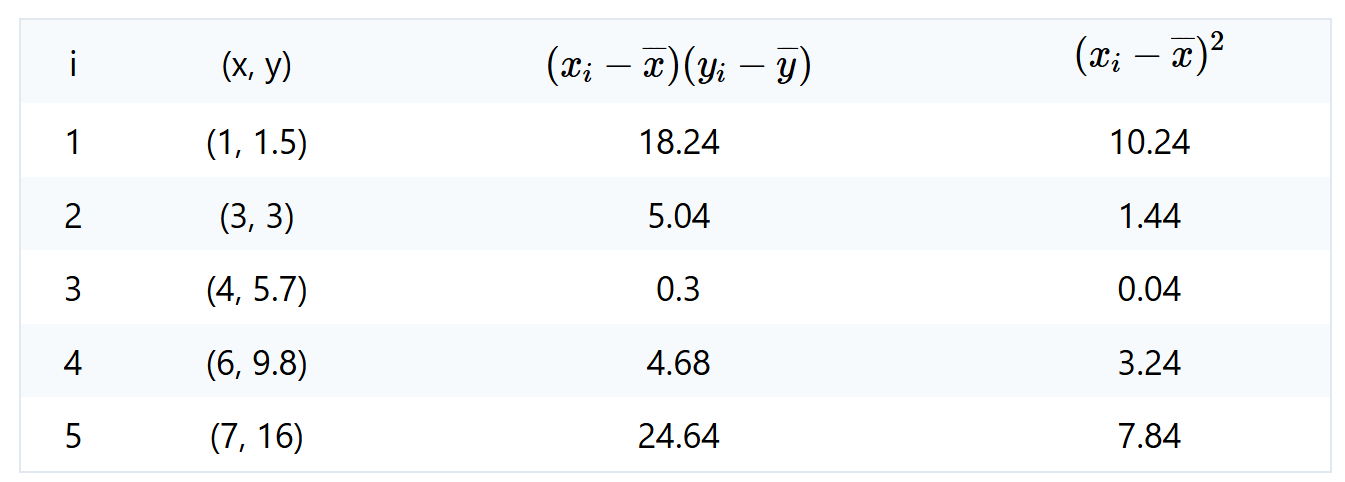
表2。根据方程式1和2计算数据点。

使用上述值，我们得到：

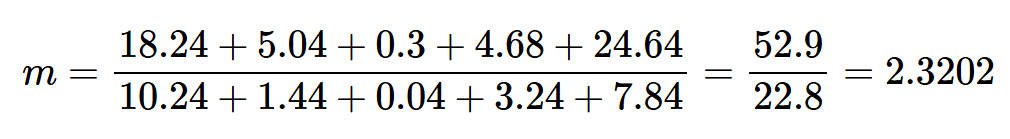
以及

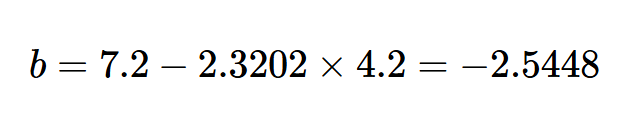
从那里，下图5提供了我们获得的线图。

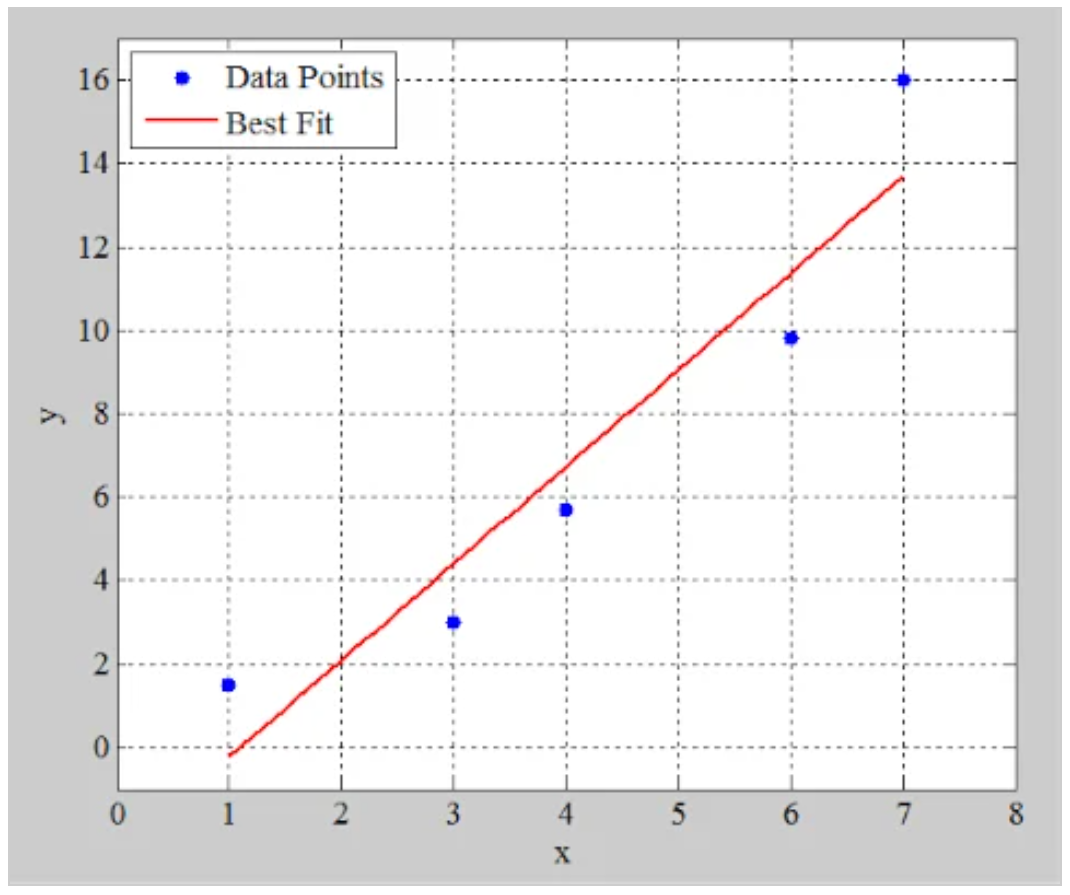
图5。使用表2计算的绘图线。

让我们找到这个新模型的残差平方和：

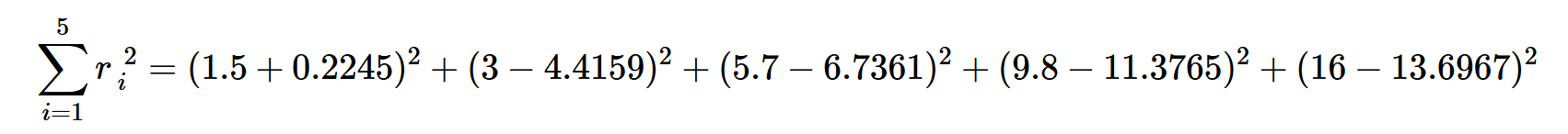
这给了我们：

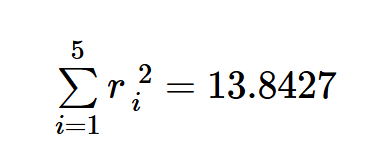
这个方程比上面获得的先前的和值小得多。最小二乘法中涉及的计算是乏味的，通常使用电子表格或计算机程序来进行这些计算。

使用Matlab寻找最佳拟合线

在Matlab中绘制曲线后，我们可以从“工具”菜单（图6（a））中选择“基本拟合”选项，打开“基本拟合（Basic Fitting）”窗口，如图6（b）所示。

图6。Matlab屏幕截图显示了“工具”菜单中的“最佳拟合”选项（A）和“最佳拟合“窗口（b）。

如果我们在“基本拟合”窗口中选择“线性”和“显示方程”，Matlab将生成并显示“最适合”我们数据点的线性方程。

K型热电偶的线性模型

继续使用Matlab，我们发现K型热电偶在0至70°C的温度范围内具有以下线性模型：

在这种情况下，模型的斜率和y轴截距分别为40.778μV/°C和13.695μV。四舍五入到两位有效数字，我们得到：

该模型和K型热电偶产生的值之间的差异如图7所示。这给了我们μV的近似误差。

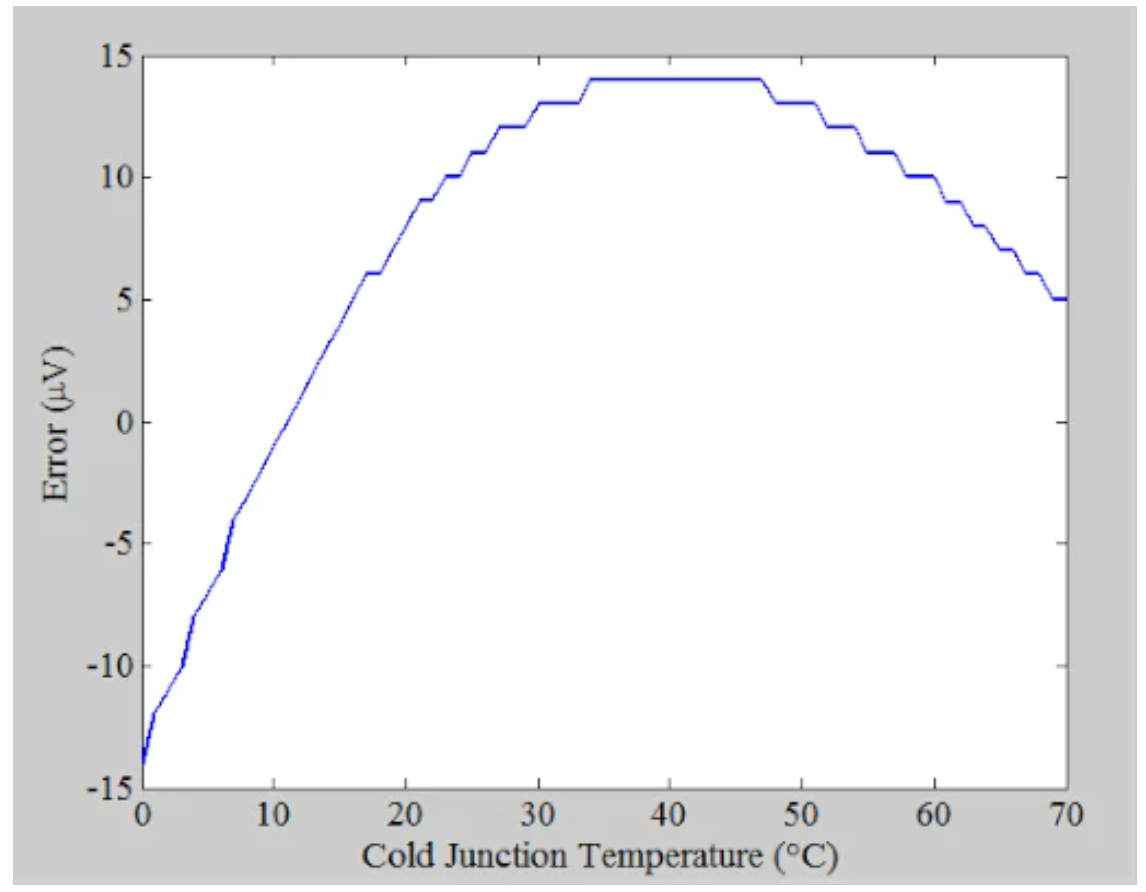
图7。显示模型和K型热电偶产生的值之间差异的图。

将这些值除以41μV/°C线的斜率，我们得到了下面绘制的以°C为单位的误差。

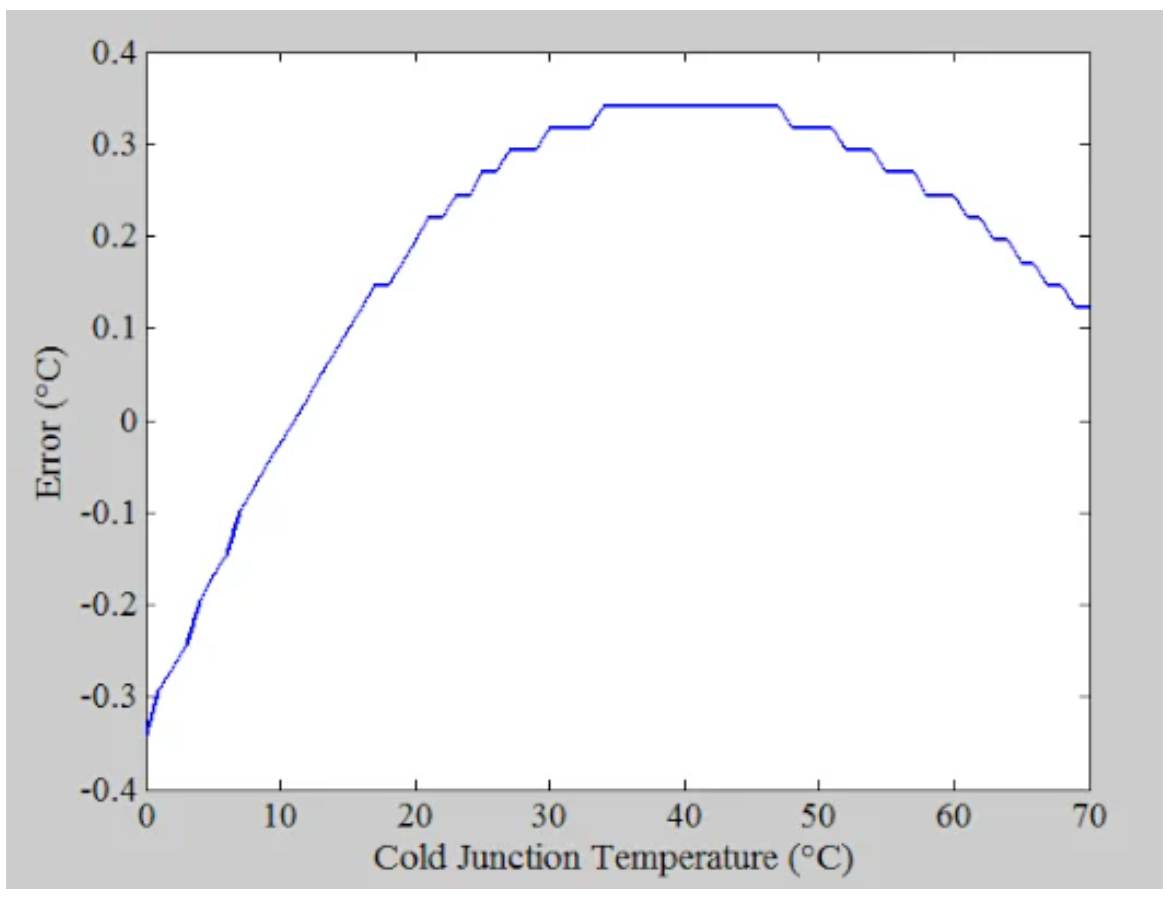
图8。显示分割前一个图的值时的变化的图。

根据最佳拟合线，当Tc从0变化到70°C时，近似误差约为0.35°C。这几乎是之前模型误差的一半。最后，请记住，如果冷端温度在设计中的变化范围更有限，则可以获得更准确的模型。例如，如果Tc从20°C变化到50°C，则最佳拟合线可以更准确地模拟热电偶响应。

对于限制Tc如何提高精度的已解决示例，TI的这篇应用说明可能很有用。