SUSAN边缘检测算法性能分析与比较
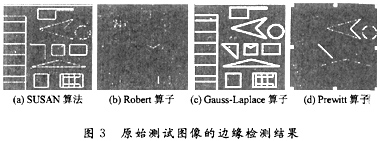


而Robert算子和Prewitt算子对部分直线边缘不能检测出来,圆的边缘也有部分漏检情况;Gauss-Laplace算子虽然基本上可以检测出所有边缘,但是他的定位效果较差,边缘象素较宽。
4.2抗噪声能力好
由于USAN的求和相当于求积分,所以这种算法对噪声不敏感,而且SUSAN算法不涉及梯度的计算,所以该算法抗噪声的性能很好。很明显,如果考虑有独立同分布的高斯噪声,只要噪声小于USAN函数的相似灰度门限值,噪声就可被忽略。对局部突变的孤立噪声,即使噪声的灰度与核相似,只要局部USAN值小于门限g,也不会对边缘检测造成影响。因此SUSAN边缘检测算法可以用于被噪声污染的图像的边缘检测。
而其他的边缘检测算法,Robert算子、Prewitt算子、Gauss-Laplace算子,以及应用广泛的Canny算子,由于这些算法都涉及一阶梯度,甚至二阶梯度的计算,所以他们的抗噪声能力较差[2-5],图4、图5也证明了这一结论。
4.3算法使用灵活
使用控制参数t和g,可以根据具体情况很容易地对不同对比度、不同形状的图像通过设置恰当的t和g进行控制。比如图像的对比度较大,则可选取较大的t值,而图像的对比度较小,则可选取较小的t值。所以这种算法非常适用于对某些低对比度图像或目标的识别。
4.4运算量小,速度快
对1幅256×256的图像,应用SUSAN算法进行计算,对每一点只需做8次加法运算,共需要做256×256×8次加法。
而对于其他的经典的边缘检测算法,如果采用欧式距离作为梯度算子,Sobel算子采用两个3×3的模板,对每一点需要做9次加法,6次乘法,以及1次开方运算,则共需要做256×256×9次加法运算和256×256×6次乘法运算,以及256×256次开方运算。对Gauss-Laplace算子、Priwitt算子以及Canny算子计算量就更大。
4.5 可以检测边缘的方向信息
SUSAN算法实际上还可以检测边缘的方向信息。具体算法是,对每一个检测点计算模板内与该点灰度相似的象素集合的重心,检测点与该重心的连线的矢量垂直与这条边缘[5]。
5 结 语
SUSAN边缘检测算法直接利用图像灰度相似性的比较,而不需计算梯度,具有算法简单、定位准确、抗噪声能力强等特点。因此,非常适于含噪图像或低对比度灰度图像的边缘检测。如果进一步减小门限g的数值,SUSAN算法还可以用于角点的检测[1]。



评论