一种准确地预测由泄漏电流引起的 PLL 基准杂散噪声之简单方法
杂散噪声而言,fm = 2 fPFD、Em = Vpk-2ndHar 且
本文引用地址:https://www.eepw.com.cn/article/201612/328184.htm用类似方法可以算出针对较高阶谐波的比值。
有源环路滤波器举例
图 7 显示了一个围绕运放建立的有源环路滤波器例子。I_Leakage 表示充电泵和运放的泄露电流之和。既然环路滤波器具有类似的结构,所以这里运用了与无源滤波器例子中相同的方法。在运放的输出端增加由 RP2 和 CP2 组成的极点,以将该器件的噪声贡献限制在LBW 的 15 或 20 倍以外,这可降低 VCO 调谐节点处的锯齿波信号幅度。应该提到的是,CP2 包括 VCO 调谐端口的输入电容。
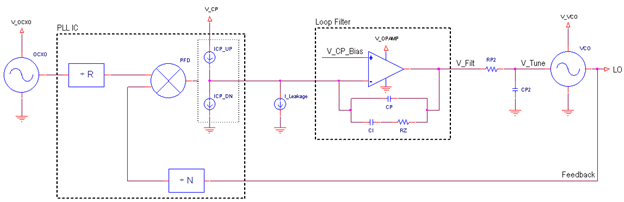
图 7: 采用有源环路滤波器的 PLL 系统,I_Leakage 代表充电泵和运算放大器的泄漏电流
锯齿波信号经过低通滤波,低通滤波的等式可以用拉普拉斯变换域 (LaplaceTransforma domain) 的基本分压等式得出,并可表示为:
其中 f 代表频率,单位为 Hz。
锯齿波信号的傅立叶级数分量自然会根据其频率不同而受到不同的影响。基准杂散噪声与载波之比变为:
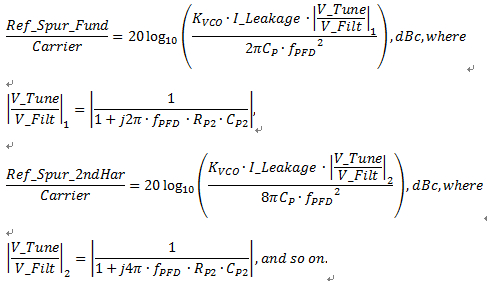
该理论的实验室验证
我们在实验室中再现了图 5 和图 7 所示的 PLL 系统。用一个精确的电源仪表在充电泵节点处引入外部电流,以清除由系统固有泄漏引起的内在基频基准杂散噪声。然后,额外给环路注入特定大小的电流,同时测量基频基准杂散噪声的大小。图 8 比较了对两种类型的滤波器所测得和所计算的值。在仪器准确度和组件容限范围内,所测得和所计算的数字是一致的。
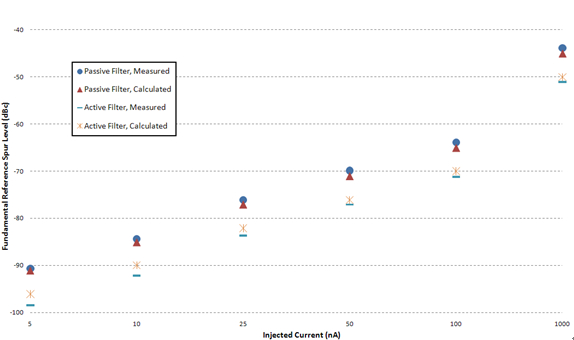
图 8:采用有源和无源环路滤波器时,所测得和所计算的基频基准杂散噪声比较
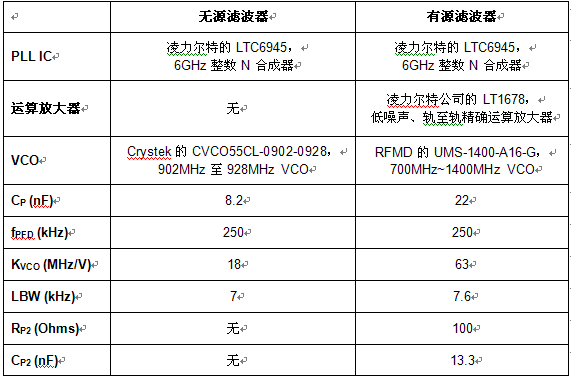
表 1 给出了用来产生图 8 测量结果的 PLL 系统之更多细节。
表 1:用来产生图 8 比较数据的 PLL 系统之细节
结果汇总
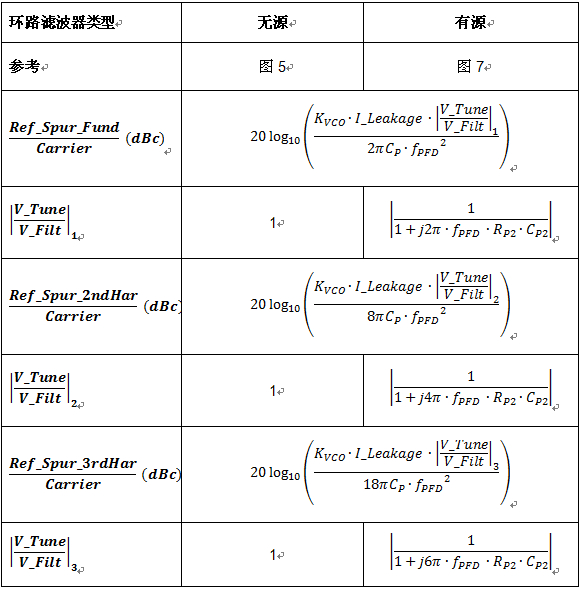
表 2 汇总了本文得出的等式。
表 2:预测直至三阶谐波的基准杂散噪声的公式
结论
在 RF 系统设计中,整数 N PLL 的工作原理和非理想性是重要课题。基准杂散噪声可能对系统总体性能造成显著的负面影响。一种简单但准确的、预测 PLL 泄漏电流引起的基准杂散噪声的模型可能成为有用的工具,可以节省时间,并减少电路板修改次数。运用本文列举的电路得到的测量值验证了推导出的模型的准确性。



评论