浮点型数据存储方式分析
也就是说我们可以认为float在小端CPU的编码方式应该是:
31<-------------------------------------------------0
S(1bit)| E(8bits)| M(23bits) |
即:
-----------------------------------------------------
ADDR0+3ADDR0+2 ADDR0+1 ADDR0
ADDR0+3ADDR0+2 ADDR0+1 ADDR0
SEEEEEEE EMMMMMMM MMMMMMMM MMMMMMMM
-----------------------------------------------------
S:表示浮点数正负,1为负数,0为正数。
E:指数加上127后的值的二进制数
M: 24-bit的底数(只存储23-bit)
需要注意,浮点数为0时,指数和底数都为0,但此前的公式不成立。因为2的0次方为1,所以,0是个特例。当然,这个特例也不用认为去干扰,编译器会自动去识别。
这样我们就可以知道前面这个题中输出的结果啦,从上面的分析可以知道一个float型的数的基本存储方式,按照上面的实现可以知道5.0的存储方式为如下的形式:
01000000101000000000000000000000
从上面的这个存储形式我们可以得到基本的整形数值时0x40A00000。进而也就知道了4个bytes中的数值大小。
这是充分利用了联合体的共享内存特性,我们改变程序如下所示:
#include
typedefuniontest
{
float a;
int i;
char c[4];
}Test;
{
float a;
int i;
char c[4];
}Test;
int main()
{
Test t;
t.a = 5.0;
printf("%f",t.a);
printf("%d",t.i);
printf("%c,%c,%c,%c",t.c[3],t.c[2],t.c[1],t.c[0]);
{
Test t;
t.a = 5.0;
printf("%f",t.a);
printf("%d",t.i);
printf("%c,%c,%c,%c",t.c[3],t.c[2],t.c[1],t.c[0]);
t.i = 65;
printf("%f",t.a);
printf("%d",t.i);
printf("%c,%c,%c,%c",t.c[3],t.c[2],t.c[1],t.c[0]);
return 0;
}
printf("%f",t.a);
printf("%d",t.i);
printf("%c,%c,%c,%c",t.c[3],t.c[2],t.c[1],t.c[0]);
return 0;
}
根据上面的分析,可以比较方便的计算出结果如下所示: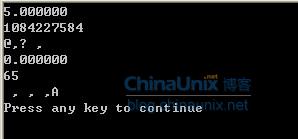




评论