数字锁相放大器的实现研究
3 数字锁相放大器的算法设计
当获得ADC的采样数据之后,DSP会对采集的数据进行相关的处理。DSP完成的主要功能有内部振荡信号的产生、数字相关运算、低通滤波以及最终相位和幅度计算。DSP会产生两路同频、正交的参考信号来锁定输入信号。目前比较常用的方法有正交迭代法和查找表法。由于定点DSP的有限字长带来的舍入误差,正交迭代法会产生较大的频率偏差。经过相关运算之后,表现为一个低频干扰信号,此信号很难被滤除掉,会对测量产生较大误差,并且正交迭代法的运算量过大,不能满足信号处理的实时性要求。本系统在FLASH中存储了正弦波的四分之一个周期的正弦值,共2 048个点,采用查找表法来产生所需要的两路正交的周期信号。
采样数据和参考信号相乘之后通过低通滤波器,滤除高频成分和噪声成分,获得所需要的两路直流分量。低通滤波器的性能是整个锁相放大器设计的关键。它的性能好坏直接决定了数字锁相放大器的性能。为了满足系统的实时性要求,低通滤波器的运算要尽可能的高效,一般的数字低通滤波器很难满足要求。
积分梳状滤波器在多速率调制系统中广泛应用,在硬件实现时不需要存储滤波器系数,也不需要乘法器,其结构简单,运算效率高,非常适合在DSP中实现。为了实现高效的窄带FIR低通滤波器,系统采用了积分梳状滤波器(Cascaded Integrator Comb Filter,CIC)结合降采样的方法。通过多级级联的结构,逐渐地降低系统的采样率,这样能够有效降低对各级抗混叠滤波器的性能要求。
积分梳状滤波器是一种特殊的FIR滤波器,其冲击响应为:

式中:R表示滤波器的阶数。积分梳状滤波器是线性时不变系统。对积分梳状滤波器的冲击响应进行x变换,可以得到积分梳状滤波器的传递函数为:

由式(8)可知,积分梳状滤波器由积分器H1(x)和梳状滤波器H2(x)级联而成。假设系统输入是x(n),输出是y(n),则:
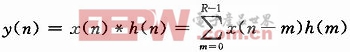

通过式(10)可以看出,积分梳状滤波器用加法运算代替了一般滤波器的乘加运算,对DSP来说运算效率大大提高。假设系统的抽取因子为D,考虑将积分梳状滤波器用于抽取系统中,相邻的两个输出为y(n)和y(n+D),其表达式为:

由式(9)可知,当滤波器的阶数R与抽取因子D相等时,滤波和抽取的过程可以用一个简单的累加运算来完成,即相邻的D个数为一组,累加求和。这种累加运算在DSP中的运算效率很高。下式是CIC的幅频响应:
当f趋近于0时,需要注意CIC滤波器增益为D,在实际运算中需要对其进行处理。设系统的采样率为fs,最终低通滤波器的截止频率为fc。若满足Dfc/fs1/64时,系统的通带容差可以忽略,实际系统中选取D=512。
单级级联的CIC滤波器幅频特性具有较高的旁瓣,可用多级级联的CIC滤波器的级联来降低旁瓣,改善阻带衰减特性。但是过度的降采样,会导致数据的损失。在考虑到对运算速度和数据量的要求,实际系统采用了一级CIC配合多级半带滤波器的方法来满足实时性要求。
在CIC滤波器之后,系统通过若干级联的半带滤波器结合2倍降采样,使低通滤波器的截止频率进一步降低。半带滤波器的通带和阻带对称,设计常采用FIR半带滤波器。半带滤波很容易实现线性相位,并且有近一半的系数精确为零,非常适合做2倍抽取,同时也非常适合进行DSP硬件运算。但是级联的2倍抽取器不应过多,通常在1到5级范围内。如果对降采样的阶数要求较高,可以适当地加大第一级的CIC降采样率来满足要求。
模拟信号相关文章:什么是模拟信号
滤波器相关文章:滤波器原理
滤波器相关文章:滤波器原理
低通滤波器相关文章:低通滤波器原理
电源滤波器相关文章:电源滤波器原理
数字滤波器相关文章:数字滤波器原理 锁相放大器相关文章:锁相放大器原理




评论