电能计量芯片Sigma-Delta ADC降采样滤波器设计（一）

由于Σ-△为二阶调制器，因此，三阶CIC 滤波器即可达得很好的抽取效果.假定延迟因子为1,则内部寄存器的长度L = (N*(log2R ) + 1) 为19bit.采样定点算法，内部寄存器量化为Sfix34. En15,输出为Sfix24. En23.由CIC 滤波器的结构以及幅值响应公式可知，当R 足够大时，信号通过CIC 滤波器时，幅值将会被放大[RM]N 倍，此设计中为643 ,因此，需将CIC输出右移18 位，消除增益对信号的影响.图3 为通过MATLAB 仿真得到FS =1792kHz, R = 64,N = 3 的归一化(0 - 0. 1)幅频特性曲线.

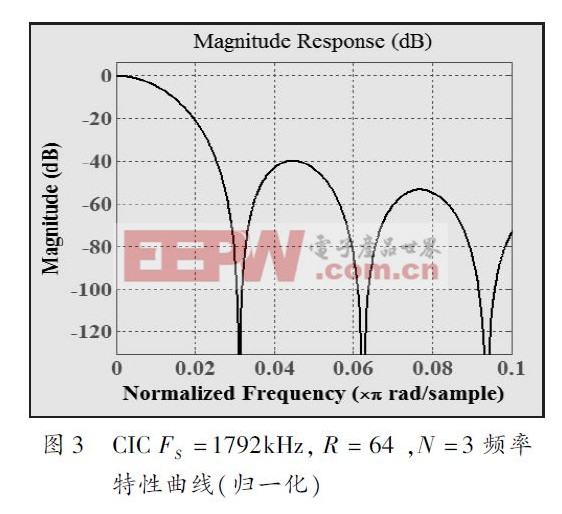
2 半带滤波器的设计

第二级的抽取滤波器用于衰减经过第一级梳状滤波器后混叠在基带内的信号分量和量化噪声分量.由于电能计量对信号有严格的线性相位要求，所以必须采用FIR 型滤波器.半带滤波器是一种特殊的线性相位滤波器，它的偶数系数都为零(中间位系数为0. 5)，因此其实现滤波的运算量与同样长度的其它线性相位滤波器相比减少一半，这将进一步减小芯片面积.降低电路的功耗.

综合考虑芯片面积以及系统的频率响应，HBF 设定为6 阶.考虑到正弦信号的高次谐波以及CIC 补偿滤波器的通带频率，HBF 的通带频率设定为2. 5kHz.

由于HBF 的系数值很少，量化精度不够将影响系统的传输特性，仿真到的系数采用Sfix48. En47 Bit,内部乘法器采用Sfix56. En55 Bit 可满足系统要求，而考虑到补码定点数加法有可能产生溢出，所以加法器量化为Sfix56. En54 Bit.图4 为通过MATLAB 仿真得到的HBF 幅频特性曲线.

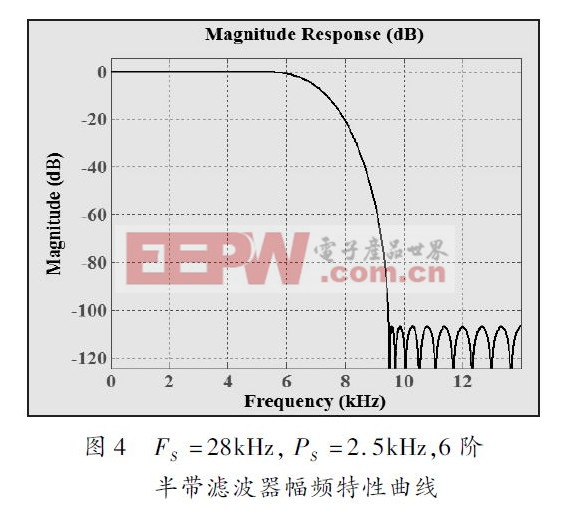
HBF 的运算包括乘法以及加法，而乘法运算的功耗最大.传统的乘法运算采用移位相加的原理，相加次数等于乘数中1 的个数，因此减少乘数中1 的个数即可降低乘法电路的功耗.CSD 编码正好满足这一要求，经过CSD 编码后，将乘法系数中1 的个数降到最低，从而减少加法(或减法)的次数.CSD 编码含三重值{1,0,-1},编码原则是从最低有效位开始，用100…0(-1) 来取代所有大于2 的1 序列.例如上述HBF中乘法系数b (3)= 0. 28847028573567002,量化后b(3)= 48′h24EC98258D1E(Sfix48_En47)，则对应的CSD 编码b (3)= 0+00+0+000-0-00+0+0-00000+0+0-0-00+0-0+00+000-0(“+”表示1,“-”表示负1).

x(n)*b(3) = – (x(n) 1) + x(n) 5 + x(n) 8 – (x(n) 10) + x(n) 12 + … + x(n) 40 + x(n) 《44,因此，经CSD 编码后， b (3)的乘法运算变成只有10 次加法和7 次减法运算，与传统的移位相加相比，减少了运算的次数，从而降低了HBF 的功耗.