基于导频的OFDM系统信道估计
其中am是信道的复数幅值,Ts为系统的采样速率。因此整个冲激响应都位于CP的长度范围之内。假设信道在一个0FDM符号内保持不变,信道的冲激响应h(t)的N点离散傅里叶变换为:本文引用地址:https://www.eepw.com.cn/article/158090.htm
![]()
设接收端经过N点离散傅里叶变化后得到的频域接收信号为:
![]()
其中XNxN表示以Xk为对角线的对角阵,N为信道中高斯白噪声的频域表示,F为N点DFT变换矩阵:

2 信道估计
2.1 LS(最小平方)信道估计算法分析
LS算法就是在不考虑噪声的条件下,估计信道的冲击响应向量hLS=[h0,h1,…,hN-1]T,使其代价函数最小。LS估计器的代价函数定义如下:
![]()

LS信道估计的特点是简单,但是从其代价函数可以看出,在找最优解时没有考虑接收信号中的噪声及子载波间的干扰,因为这种算法估计出的信道对接收信号进行但抽头复系数均衡时,输出信号的均方误差较大,准确度受到限制。
2.2 MMSE(最小均方误差)信道估计算法分析
MMSE信道估计算法对于ICI(子载波间干扰)和高斯白噪声有很好的抑制作用,它是在LS估计的基础上进行的:
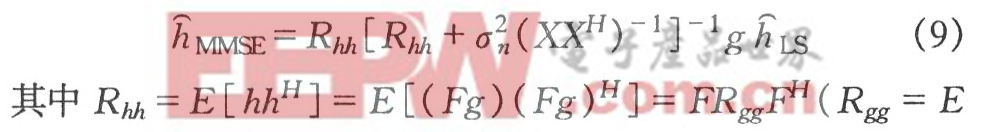
[ggH)为信道频率响应的N阶自相关矩阵,σn2为信道噪声方差。由式(9)可知,MMSE算法的运算量要比LS算法大的多,随子载波数N呈指数增长,并需随导频信号X的变化实时进行矩阵的逆运算((XXH)一1),导致系统效率很低。
3 改进的LS算法
由式(6)可得:







评论