基于工频畸变技术的抄表系统
2 硬件电路设计
调制电路系统主要由滤波电路、过零检测电路及调制电路组成。调制电路的等效电路已给出,不再讨论。图3所示硬件电路是由A1(MAX-291)、 A2(TA7504P)、A3(OP07)组成的滤波电路和过零检测电路。A1通过改变时钟输入频率可改变滤波器截止频率,并且截止频率为时钟频率的 1/100。时钟输入端加5 V电平的方波信号,在A1的输入(IN)与输出(OUT)端之间可以获得低通滤波器的特性。A2用于平滑A1的输出阶梯状波形,增强其效果。过零检测电路主要由运放器OP07,4个二极管以及1个三极管组成。
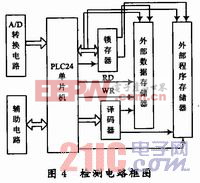
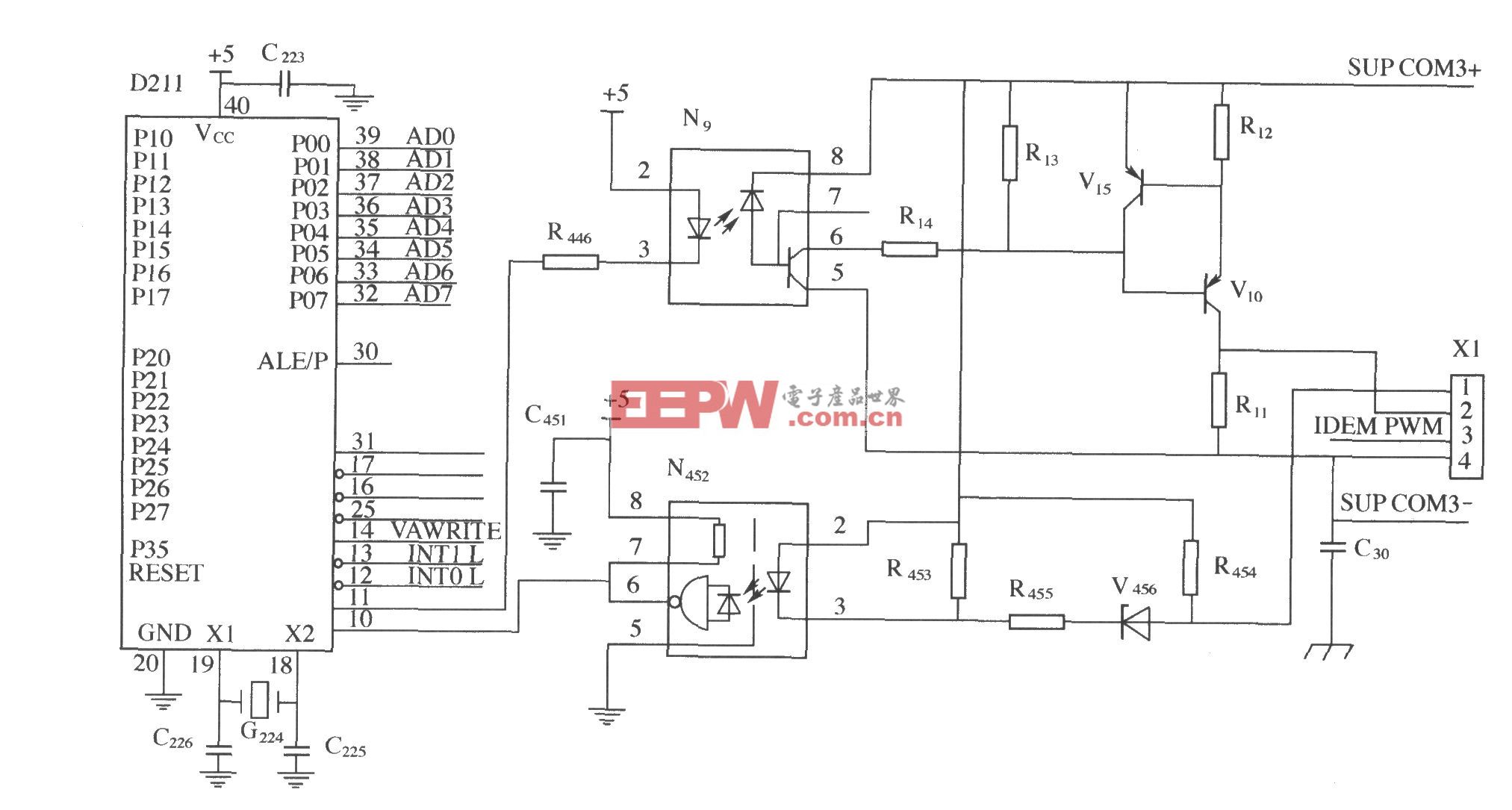
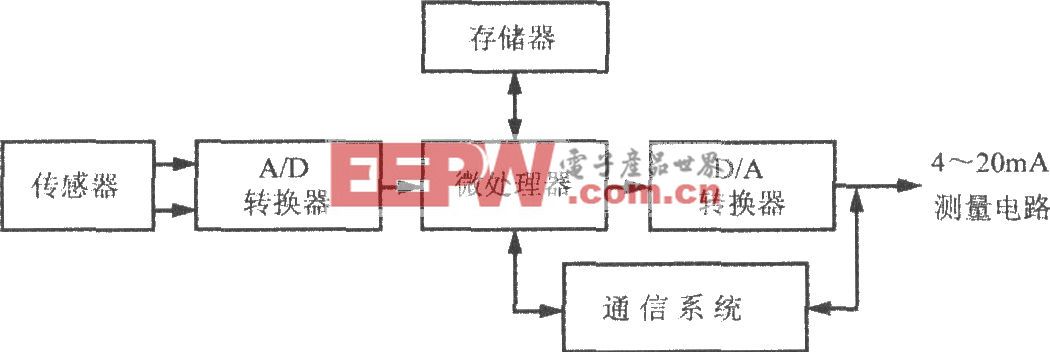
畸变信号的检测电路由前置滤波电路、数据采集电路、数据处理电路组成。数据采集电路由ADl674芯片及其外围电路组成。整个检测系统核心是一块 PLC24系列微处理器芯片加上必要的数据存储器、程序存储器及必要的输入、输出电路组成的单片机系统。单片机技术已经非常成熟,在此只给出如图4所示的系统框图。
3 信号检测
信号检测是一个判断过零点处有无畸变的问题。目前国内一般采用数字差分技术(Digital Differential Technique)进行检测,即前一次的采样值与当前的采样值进行做差运算。
如果F(t)=A1 sin(ω1t),T是其周期Tper的整数倍,则d(t1)≡0。从这个结果可以看出,由式(1)所描述的数字差分技术应用到具有稳定周期的周期信号时,其差分结果恒等于O。但由于电网信道环境复杂,其中充斥了大量的谐波分量和噪声的干扰,使得理论上十分可行的数字差分技术在实际运用中效果却并不理想。
本文采用的小波检测法是时频分析的有力工具。信号x(t)的连续小波变换为:
式中:a为伸缩尺度因子;b为平移因子。离散小波函数ψj,k(t)可表示为:
为了使小波变换具有可变化的时间和频率分辨率,需要改变a,b的大小,使小波变换具有“变焦距”的功能。实际中,广泛应用的是二进制离散小波,即用二进制动态采样网格,a0=2,b0=1,每个网格点对应的尺度为2j,而平移为2jk。由此得到的小波ψj,k(t)被称为二进小波(Dyadic Wavelet)。
二进小波对信号的分析具有变焦距的作用。假定开始选择一个放大倍数2-j,它对应为观测到信号的某部分内容。如果要进一步观看信号更小的细节,就需要增加放大倍数,即减小j值;反之,则减小放大倍数,即加大j值。任意信号都可以表示成式(5)形式:

j和k的取值均在±∞,意味着在所有尺度上做细化处理,补充细部特征。在用尺度的观点分析各种信号时,超过某一特定的尺度(例如j0)后,细部特征就不再起作用了,这时可将式(5)以尺度j0为界限分成两部分,j0以下各尺度作为细化特征的近似;j0以上的各尺度用于基本特征的提取。用滤波的观点就是j0 以下各尺度对应于中心频率不同的带通滤波器组,j0以上各尺度对应于带宽不同的低通滤波器组。式(5)可表示为:等式右边第一部分可看作信号x(t)的尺度为2j0的逼近低频信号;第二部分可看作是x(t)的细节高频信号。任意一个尺度的逼近信号均可表示成下一尺度的逼近信号和细节信号之和。




评论