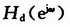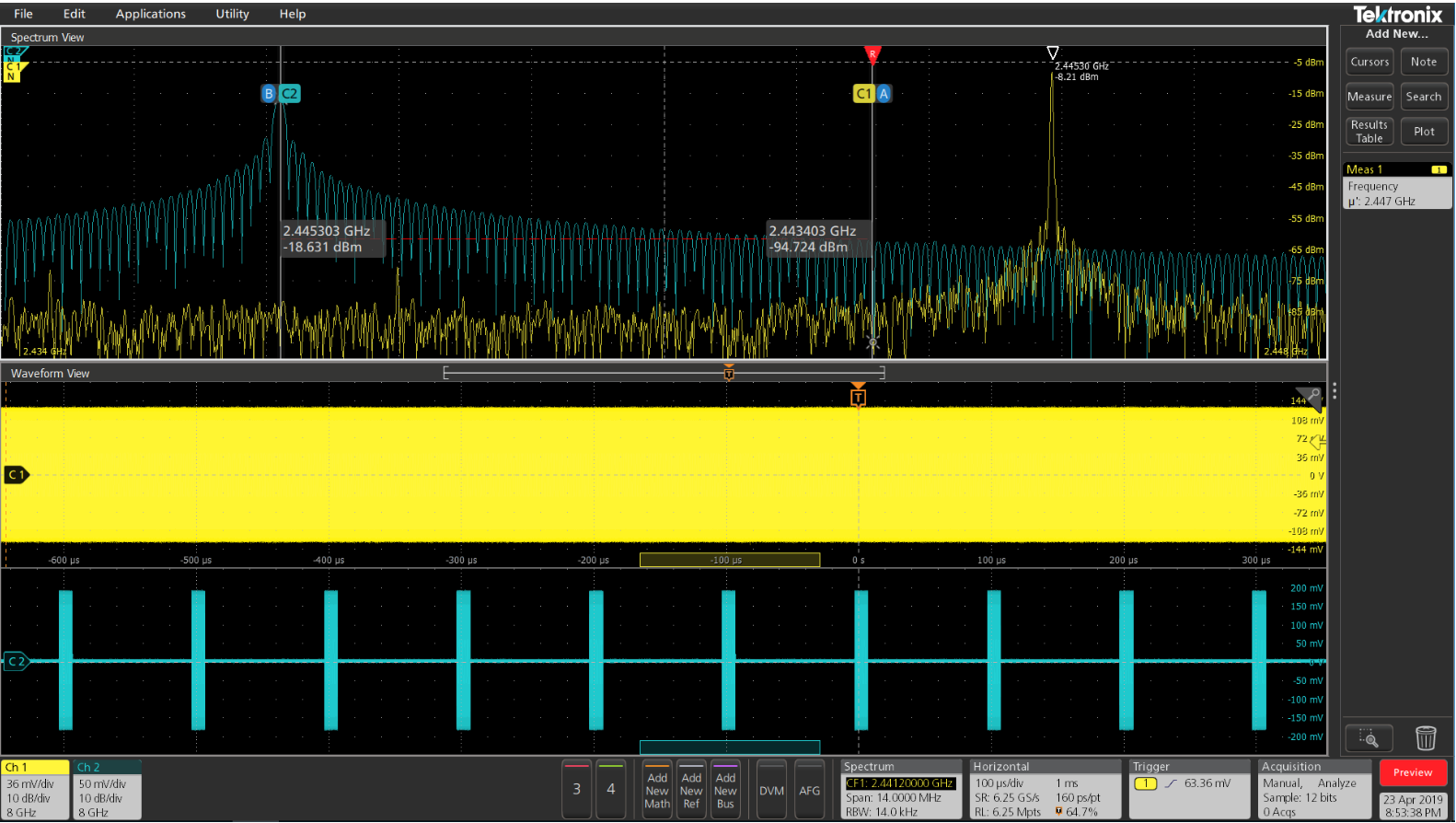
- 快速傅里叶变换 (fast Fourier transform) 简称FFT, 是利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。一直以来,我们接受的教育就是要用FFT来进行频域信号的测试与分析。工作以后我们利用示波器上的FFT功能进行频域信号测试。FFT功能在示波器普及率高,易获取。可以实现时域、频
- 关键字:
傅里叶变换 示波器 多通道分析
- 1.4 傅立叶级数展开 之前我们在介绍泰勒展开式的时候提到过傅立叶级数。利用傅立叶级数对函数进行展开相比于泰勒展开式,会具有更好的整体逼近性,而且对函数的光滑性也不再有苛刻的要求。傅立叶级数是傅立叶变换的基础,傅立叶变换是数字信号处理(特别是图像处理)中非常重要的一种手段。遗憾的是,很多人读者并不能较为轻松地将傅立叶变换同高等数学中讲到的傅立叶级数联系起来。本节我们就来解开读者心中的疑惑。 如果你对本文涉及的基础问题不甚了解,那么建议你阅读本文前面的部分。希望读者能日积月累,夯实基础。
- 关键字:
傅里叶变换 小波
- 这一系列的文章中间中断了很久,很多朋友也留言希望我继续连载完,遂“重拾旧河山”,希望如果有时间能够把它做完。 本节我们介绍欧拉公式,它是复变函数中非常重要的一个定理,同时对于傅立叶变换的理解也必不可少。我们在高等数学里学习的傅立叶级数通常都是用三角函数形式表示的,而傅立叶变换中的一般都是用幂指数形式的,欧拉公式的作用正是把三角函数与e的幂指数联系到一起。 如果你对本文涉及的基础问题不甚了解,那么建议你阅读本文前面的部分。 完全搞懂傅里叶变换和小波(1)——总纲 http://www.eepw.
- 关键字:
傅里叶变换 小波
- 书接上文,之前我们介绍了高等数学里的三个中值定理,本节我们继续按照总纲的思路,用柯西中值定理来证明泰勒公式。这是我们循序渐进引出傅里叶的最后一项任务,完成这一步的学习之后,你就可以从级数的角度,了解傅里叶的意义了。 完全搞懂傅里叶变换和小波(1)——总纲 http://www.eepw.com.cn/article/201703/344766.htm 完全搞懂傅里叶变换和小波(2)——三个中值定理 http://www.eepw.com.cn/article/201702/344594.htm
- 关键字:
傅里叶变换 小波
- 书接上文,本文章是该系列的第二篇,按照总纲中给出的框架,本节介绍三个中值定理,包括它们的证明及几何意义。这三个中值定理是高等数学中非常基础的部分,如果读者对于高数的内容已经非常了解,大可跳过此部分。当然如果你需要对傅里叶变换有一个更深刻的认识,或者说从数学角度一点一滴完全搞懂它,为了体系的完整性,这部分知识还是必须的。 上篇文章链接地址:完全搞懂傅里叶变换和小波(1)——总纲 http://www.eepw.com.cn/article/201702/344594.htm 由于公式较多,这里只能
- 关键字:
傅里叶变换 小波
- 无论是学习信号处理,还是做图像、音视频处理方面的研究,你永远避不开的一个内容,就是傅里叶变换和小波。但是这两个东西其实并不容易弄懂,或者说其实是非常抽象和晦涩的! 完全搞懂傅里叶变换和小波,你至少需要知道哪些预备知识?主页君从今天开始就将通过一些列文章告诉你他们之间的来龙去脉!本节是全部系列文章的第一节——总纲,日后我们也将按照这个思路一点一点讲述所有的知识。需要说明的是,本文主要面向计算机专业或者电子信息专业的读者,为此我们将尽量采取一些非常非常基础的知识来帮助你理解。所以,题目里面讲的“完全搞懂
- 关键字:
傅里叶变换 小波
- 随着超声波技术的发展,超声波在风速测量、流体的流速和流量的测量中起到了重要作用。目前,采用超声波进行风速测量的方法主要有超声波时差法、多普勒法、相关法、卡门涡街原理、相位差法和超声波频率差法。超声波时
- 关键字:
风速风向 DSP 相关函数 傅里叶变换
- 傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量)。
傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
傅里叶变换是一种解决问题的方法,一种工具,一种看待问题的角度。理解的关键是:一个连续的信号可以看作是一个个小
- 关键字:
傅里叶变换 拉普拉斯变换
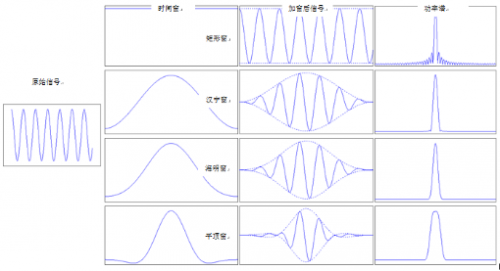
- 摘要:在信号分析时,我们一般会截取有限的波形数据做傅里叶变换,这个截断过程会产生泄漏,导致功率扩散到整个频谱范围,产生大量“雾霾数据”,无法得到正确的频谱结果。虽然知道加窗可以抑制泄漏,但复杂的窗函数表达式及抽象的主瓣旁瓣描述方法,另人更加迷惑,下面我们抛弃公式用通俗易懂的方式介绍窗函数的选择。 1.加窗与窗函数 在数字信号处理中,常见的有矩形窗、汉宁窗、海明窗和平顶窗,这里不再赘述窗函数的表达式,只讨论窗函数的使用,下图直观地描述了信号加窗的过程及窗函数基本特征。
- 关键字:
窗函数 傅里叶变换
- 简介:本文介绍了在实际工程中常用到的傅里叶变换和Z变换之间的关系、各自的意义等内容。
傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量)。
傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
傅里叶变换是一种
- 关键字:
傅里叶变换 拉普拉斯变换 变换

- 学习傅里叶变换需要面对大量的数学公式,数学功底较差的同学听到傅里叶变换就头疼。事实上,许多数学功底好的数字信号处理专业的同学也不一定理解傅里叶变换的真实含义,不能做到学以致用!
事实上,傅里叶变换的相关运算已经非常成熟,有现成函数可以调用。对于绝大部分只需用好傅里叶变换的同学,重要的不是去记那些枯燥的公式,而是解傅里叶变换的含义及意义。
本文试图不用一个数学公式,采用较为通俗的语言深入浅出的阐述傅里叶变换的含义、意义及方法,希望大家可以更加亲近傅里叶变换,用好傅里叶变换。
一伟大的傅
- 关键字:
傅里叶变换
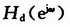
- 有限长脉冲响应(FIR)数字滤波器由于设计灵活,滤波效果好以及过渡带宽易控制,因此在数字信号处理领域得到了广泛的应用。FIR数字滤波器的典型设计方法主要有窗函数法和频率采样法。正确理解和掌握这两种设计方法是学习FIR数字滤波器的一个重要环节。用窗函数法进行FIR滤波器设计的相关问题,目前的教材讲解较为细致,这里不再赘述。本文主要探讨用频率采样法设计FIR数字滤波器的相关问题,主要包括设计原理、性能分析、线性相位条件及设计中应注意的问题等几个方面。
1 设计原理及滤波器性能分析
频率采样法是
- 关键字:
FIR滤波器 傅里叶变换
- 近红外光谱分析技术近年来巳成功应用于食品、烟草、药品及化工等诸多行业产品的分析测定,特别在农副产品的品...
- 关键字:
傅里叶变换 红外光谱分析 化学测定
- 摘要 基于Good—Thomas映射算法和ISE快速傅里叶变换IP核,设计了一种易于FPGA实现的24点离散傅里叶变换,所设计的24点DFT模块采用流水线结构,主要由3个8点FFT模块和1个3点DFT模块级联而成,并且两级运算之间不
- 关键字:
FPGA 离散 傅里叶变换 结构设计
傅里叶变换介绍
傅里叶变换-正文 一种积分变换,它来源于函数的傅里叶积分表示。积分
(1)
称为? 的傅里叶积分。周期函数在一定条件下可以展成傅里叶级数,而在(-∞,∞)上定义的非周期函数?,显然不能用三角级数来表示。但是J.-B.-J.傅里叶建议把?表示成所谓傅里叶积分的方法。 设?(x)是(-l,l)上定义的可积函数,那么在一定条件下,?(x)可以用如下的傅里叶级数来表示:
(x [
查看详细 ]
关于我们 -
广告服务 -
企业会员服务 -
网站地图 -
联系我们 -
征稿 -
友情链接 -
手机EEPW
Copyright ©2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《电子产品世界》杂志社 版权所有 北京东晓国际技术信息咨询有限公司

京ICP备12027778号-2 北京市公安局备案:1101082052 京公网安备11010802012473