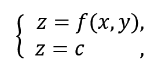
- 一 前置知识 拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题。在介绍拉格朗日乘子法之前,先简要的介绍一些前置知识,然后就拉格朗日乘子法谈一下自己的理解。 1.梯度 梯度是一个与方向导数有关的概念,它是一个向量。在二元函数的情形,设函数f(x,y)在平面区域D内具有一阶连续偏导,则对于每一点P(x0,y0)∈D,都可以定义出一个向量:fx(x0,y0)i+fy(x0,y0)j&n
- 关键字:
机器学习 拉格朗日
拉格朗日介绍
您好,目前还没有人创建词条拉格朗日!
欢迎您创建该词条,阐述对拉格朗日的理解,并与今后在此搜索拉格朗日的朋友们分享。
创建词条
关于我们 -
广告服务 -
企业会员服务 -
网站地图 -
联系我们 -
征稿 -
友情链接 -
手机EEPW
Copyright ©2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《电子产品世界》杂志社 版权所有 北京东晓国际技术信息咨询有限公司

京ICP备12027778号-2 北京市公安局备案:1101082052 京公网安备11010802012473