基于GWO-BP-CNN-ec的风电功率短期预测模型*
0 引言
风力发电随着成熟的技术及丰富的资源发展愈发迅速。因其高利用率及就地可取的便捷性逐渐成为国内主要发电方式之一。因大规模风电并网影响电力系统稳定性的问题日益凸显,加之风的不确定性、间歇性导致风电机组无法全方位捕捉风能,所以风电功率预测的精准及迅速性对短期功率预测起到极其重要的作用。短期功率预测技术可以预测短时间内的发电量,预测值间隔可以控制在分钟或小时级时间范围内。因为风的短期突增或间歇为极大程度上影响发电量,对电网有一定影响,所以短期风电功率预测对于风电并网来说非常重要。
本文提出了一种风电短期功率预测的深层神经网络组合模型的算法。通过对采集西北某风电场的历史观测数据、数值天气预报(Numerical Weather Prediction,NWP)数据进行建模、分析。再将数据进行离散,将采集的风电数据转型成为卷积神经网络的海量输入。然后结合灰狼优化算法对搭建的卷积神经网络模型的参数进行初始化优化。最终采用BP神经网络对整个组合模型微调后对预测值再进行偏差二次修正,最终得出GWO-BP-CNN-ec的风电功率预测组合模型。通过仿真分析得出,基于GWO-BP-CNN-ec的组合模型预测效果优于单一CNN,GWO-CNN及GWO-BP-CNN,然后对比了基于BP、Elman、小波神经网络的浅层网络预测模型与基于CNN的深层网络组合预测模型的预测效果,验证出了深层CNN网络在预测方面的精度优势,在高风速段时尤为明显。证明深层卷积神经网络组合模型对风电短期功率预测精度的提升有显著作用。
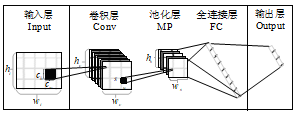
图1 卷积神经网络结构图
1 GWO-BP-CNN-ec模型原理
1.1 卷积神经网络原理
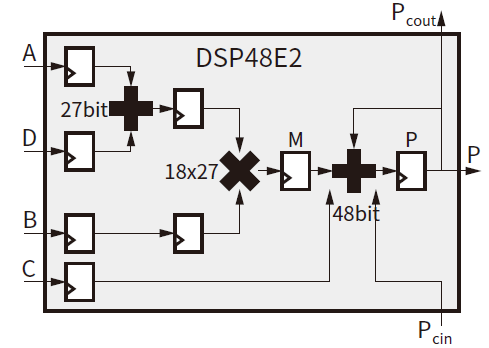
卷积神经网络结构相比于传统神经网络多了卷积、采样层。独有的参数共享机制,即卷积层与输入层用全连接的方式对应,且与其他几哥网络层中每一个单元的链接权重是唯一的。CNN中神经元可以通过共享局部权值来提取特征值。使得提取过程中每个神经元的连接权重不变,神经元组合可以更好地构成完整特征,网络的复杂度会因此降低。图1为卷积神经网络结构图。
CNN网络的学习方法如下:
假设样本在网络输出层损失函数e为
(1)
式中,n为网络输出层神经元的个数,ok为第k个神经元上的输出,yk为目标函数的理想输出。
将损失函数e对第k个神经元输出ok求偏导
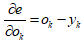 (2)
(2)
接下来将损失函数e对特征层求偏导
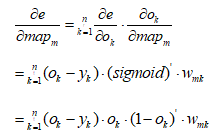 (3)
(3)
式中,mapm表示最后的特征层(即输出层的输入),wmk表示为隐含至输入的权重。因此,调整算子为
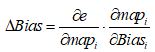
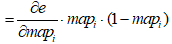 (4)
(4)
式中,mapi为对应层输出,Bias表示对应层偏置。
卷积核的计算本质上就是相乘求和加权的过程。因此,对卷积层中卷积核的调整算子为
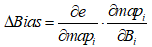
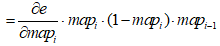 (5)
(5)
式中,mapi-1表示该层输入,也是上一层的输出。
1.2 灰狼优化算法原理
根据灰狼捕猎的动作行为,采用灰狼优化算法(Grey Wolf Optimizer,GWO)对目标最优解进行追踪。在GWO算法中,分为主狼和灰狼,假若标记主狼为α,灰狼为β,δ和ω,则主狼α一直会处于无限接近最优值的位置;而β、δ灰狼次之,等待α狼并无限接近于α狼,是其替代者;剩下的为ω狼。在整个算法流程中,α狼带领狼群搜索、跟踪、接近猎物,β、δ狼对猎物进行攻击,ω狼对猎物进行围捕。当猎物移动时,狼群形成包围猎物的圈也随之移动,直至捕获猎物。
根据灰狼捕猎的动作行为,可以将其过程分为三个阶段:包围、追捕、攻击。最优解为抓捕到猎物。具体算法描述如下:
包围:包围过程中猎物与灰狼之间的距离可表示为
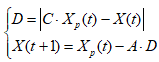 (6)
(6)
式中,D为灰狼和猎物之间的距离,t为迭代次数,Xp(t)为第t次迭代后猎物的位置(即最优解的位置),Xp(t)为第t次迭代后灰狼的位置(即潜在解的位置),A和C为系数因子。A和C计算公式为
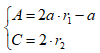 (7)
(7)
式中,α随着迭代次数的增加从2到0呈线性递减,r1,r2为[0,1]间的随机数。
追捕:β,δ狼在α狼的带领下对猎物进行追捕,根据α,β,δ的更新的位置来重新确定猎物(最优解的位置。更新方程如下
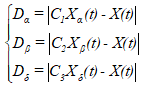 (8)
(8)
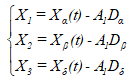 (9)
(9)
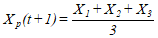 (10)
(10)
式中,Dα,Dβ,Dδ分别表示α,β,δ狼与ω狼(其他个体)之间的距离。
攻击:当式(7)中的α值从2线性递减0时,其对应的A的值也在区间[−α,α]变化。当 A∈[−1,1]时,则表明狼群趋近于猎物;当1<|A|≤2时,狼群会远离猎物,导致灰狼算法失去最优解位置,从而陷入一个局部最优的过程。灰狼优化算法流程图如图2所示。
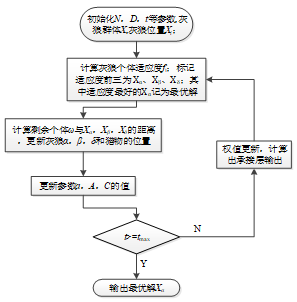
图2 灰狼优化算法
1.3 偏差修正算法原理
传统的偏差修正(Error correction,EC)通过建立偏差预测模型,使计算出的一次偏差进行二次修正处理,使得最终预测精度进一步提高。在偏差修正中,算法的核心因子即修正因子。本文通过气象背景的偏差选取历史相似时刻的偏差,再进行偏差分析,相关系数计算公式如下
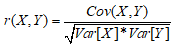 (11)
(11)
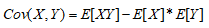 (12)
(12)
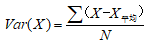 (13)
(13)
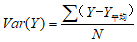 (14)
(14)
式中,Cov(X,Y)为X与Y的协方差,Var[X ]为X的方差,Var[Y ]为Y的方差,E[X ]、E[Y ]分别为X、Y的数学期望。
为了避免模型选取带来的误差,通过中位数法、排序聚类法、拟合法对预测偏差进行分析建模,并进行加权平均,并初次预测的结果值再次进行偏差二次修正,流程图如图3所示。
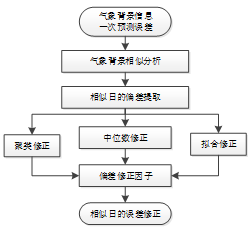
图3 修正算法流程图
偏差修正算法的具体步骤为:
(1)数据的输入。输入模型以实际风场的实际数据序列作为基准量,如:风速、预测功率、装机容量、时间标签等。
(2)提取相似时刻数据。通过提取日相同时刻的时间标签,找寻相似时间数据。对相似时刻的同一历史时间的预测功率进行修正限定。
(3)相似时刻误差的修正。利用三种方法对偏差量进行数据分析,计算相似时刻的偏差量后取平均值。一般采用排序聚类法、中位数法、拟合法,
分别得到中位数矩阵、拟合系数矩阵、分类矩阵。
(4)预测功率的修正过程。相似时刻聚类中位数对预测值的修正,为排序聚类修正;相似时刻预测功率与对应中位数的加权,为中位数修正;相似时刻拟合系数对预测功率的修正,为拟合修正;最终将预测修正值加权求平均,得到最终组合模型的精确值。
(5)输出历史相同时刻矩阵、中位数矩阵、拟合系数矩阵、聚类矩阵。
2 组合预测模型构建
2.1 模型的输入与离散化
CNN模型的输入需要海量数据且至少3维度以上。由于风电数据一般呈现2个维度,所以需将风电数据进行离散化作为CNN模型的输入量。这样不仅能满足模型海量输入数据的需求,同时还能最大化显示风电功率的特征信息。
具体离散办法为:
(1)确定离散维度。风速在空间、时间上分别离散,形成空间风速二维标签及时间三维标签。
(2)时间上的离散。将某时刻风速在其附近15分钟时间段内离散化。
(3)空间离散。将风电场单台风机点作为风速采集点,以达到对风速在空间上进行离散的目的。采集的风速数据,离散其在空间各个风速采集点上的瞬时风速,空间离散的公式如下
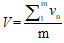 (15)
(15)
式中,V为平均风速,vn为n点瞬时风速,m为风机台数。
由于各点的瞬时风速会在平均风速附近上下波动,因此需要界定瞬时风速段,根据经验给出了在某平均风速下瞬时风速段为0.5V~1.5V。图4为离散前后风速对比图。
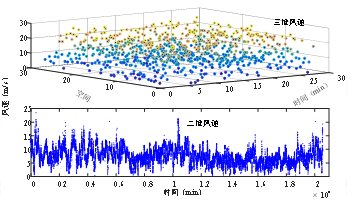
图4 离散前后风速对比图
图4中的三维风速为在某时刻下的离散风速,在该时刻下,风速被离散到28×28的矩阵中,表明该风电场有28台风机,即28个风速采集点。二维风速下,共记录了21000多个数据,将其离散化,形成了28×28×21000矩阵的三维风速。
2.2 模型的训练与参数优化
权值和阈值需要通过GWO对其进行初始化寻优。将学习率的寻优范围为[0,2],批次大小的寻优区间在[16,128]内,迭代次数的寻优范围为[1,50]内的整数,规定超参数的寻优范围以提高超参数对模型的适应度。
2.3 模型预测
由于CNN模型多用于分类问题,因此在模型检验环节,需要将模型的输出分类模式改为预测模式,将输出层的输出结果直接作为BP网络的输入。由于CNN模型的输出层为全连接,因此可以将CNN模型的输出层直接作为BP网络的输入层,通过BP网络的训练和测试来达到对整个网络的微调。
2.4 二次修正与误差分析
通过组合模型对输入风量数据的预测,会到的一组功率的预测值。建立偏差修正模型将功率的预测值、实际值、风速值输入到偏差修正模型中,通过偏差修正对于预测功率值的二次修正,可以得出偏差修正后的误差和预测功率。偏差预测的精度采用Rmse作为评价指标,通过比较修正前误差及修正后误差,得出两种模型的预测精度,作为分析对比的依据。
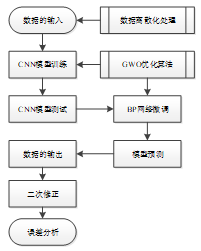
图5 GWO-BP-CNN-ec组合预测模型流程图
3 算例分析
因为卷积神经网络的输入需要大量的数据,所以本次通过收集西北某风电场的30000条数据作为CNN的输入进行模型的训练,后选取其中1000条数据进行测试。
分别对单一BP-CNN、GWO-BP-CNN、GWO-BP-CNN-ec三种模型分别进行风电功率预测。
首先,对基于CNN的风电预测模型进行仿真并分析,CNN的参数采用模型的默认值,其中训练次数为1,学习因子设定为1,批次训练量为500,BP微调部分的参数也采用模型默认值,其中学习因子和训练次数为1,批次训练量为500。通过Matlab仿真得到对比图如图6所示。
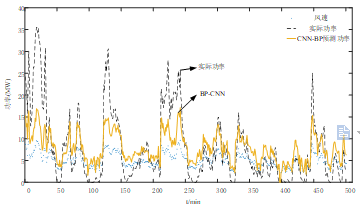
图6 BP-CNN预测值与实际值对比图
为了继续验证CNN的实际预测效果,利用GWO优化算法对CNN的参数进行初始化优化,优化后的参数为:CNN训练次数为1,CNN批次训练量为5000,CNN学习因子0.2,BP训练次数为20,BP学习因子为0.03,BP批次训练量为200。通过仿真得到如图7的仿真对比图。
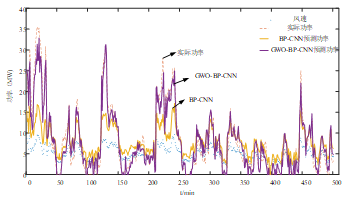
图7 GWO-BP-CNN预测值与实际值对比图
图7示GWO-BP-CNN模型预测曲线已经接近真实值,但还需要继续降低预测误差。在GWO-BP-CNN组合模型基础上,再次加入偏差二次修正。使模型得出的预测值再次进行二次修正,以进一步缩小预测误差。
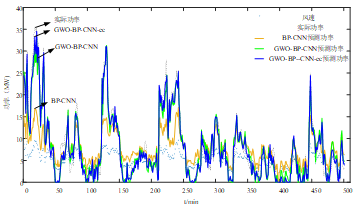
图8 GWO-BP-CNN-ec预测值与实际值对比图
通过图8的仿真结果曲线可以发现,基于GWO-BP-CNN的风电组合预测模型的绿色预测值曲线更能很好的拟合虚线实际值曲线。再加上偏差修正算法后,蓝色的预测值曲线较之前有更高的拟合度。尤其是在15-30的高风速段拟合度几乎重合,蓝色预测曲线更加接近实际值,说明了误差修正对于组合模型来说能进一步提高预测精度。
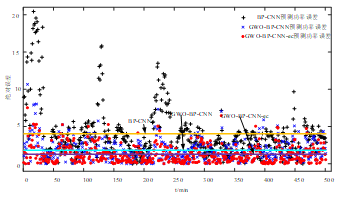
图9 CNN不同预测模型下的绝对误差
通过图9、10的误差分布图可以看出,基于GWO-BP-CNN-ec的组合模型较之前单一模型的均方根误差低,由此可见基于GWO-BP-CNN-ec的组合模型拥有更高精准地预测性能。
表1 不同模型的预测误差统计
预测模型 | 绝对误差 E(MW) | 均方根误差 Rmse |
BP-CNN | 4.0236 | 0.0979 |
GWO-BP-CNN | 1.8125 | 0.0472 |
GWO-BP-CNN-ec | 1.2841 | 0.0361 |
通过表1的预测误差可以看出,通过组合建模得到的预估效果要远好于单一CNN的模型预测方法。表1中均方根误差分别下降了0.0505和0.0618,绝对误差分别下降了2.2111MW和2.7395MW。两种预测模型的误差均下降,精度有所提高。说明了基于GWO-BP-CNN-ec的组合模型的预测精准度更高。
为了再次证明基于GWO-BP-CNN-ec的预测精度高于其他模型。将BP、Elman、WNN三种浅层神经网络预测模型的预测曲线值和基于CNN的深层神经网络预测模型的预测曲线值对比,如图11所示。
图11为经过GWO算法对参数优化后的深层、浅层网络预测效果对比,可以看出,基于GWO-BP-CNN-ec的预测曲线能更好的拟合实际曲线,尤其在高风速段时,GWO-BP-CNN-ec模型能很好将功率预测上去,从而较大幅度的降低预测误差,这也是深层网络对比于浅层网络的预测优势。一方面,深层网络的输入量更大,另一方面,深层网络在训练过程能很好的提取数据的特征量,两方面的原因使得深层网络的预测效果优于浅层网络。
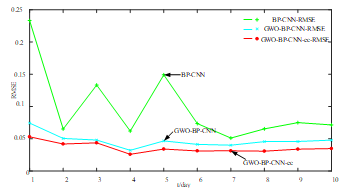
图10 CNN不同预测模型下的均方根误差
4 结论
本文在单一神经网络短期功率预测的基础上提出了一种基于神经网络组合模型的预测方法。该算法以CNN及偏差修正为核心,结合GWO对参数进行优化,最后通过BP神经网络对整个组合模型算法进行微调,最终形成一种超短期风速预测混合模型,通过实例分析得出的结论如下:
1) 本文所提的GWO-BP-CNN-ec模型在对风速的预测性能明显优于基准单一BP、Elman、WNN风速预测模型。
2) 经GWO优化及偏差修正的模型的风速预测精度比未经优化的风速预测精度高,验证了GWO优化与偏差修正的有效性。
3) 本文所提模型能够实现不同分位下的高精度短期风速预测,且能够随着分位变化产生较明显的预测值变动,进一步说明了GWO-BP-CNN-ec的有效性。考虑最优预测精度不会固定在某一个分位上,而是随着样本的变化而不同。为充分利用上述多个分位下的预测值,此后将考虑对不同分位下的预测值进行加权整合,形成加权分位回归鲁棒极限学习机来进行短期风速预测,以给系统决策者提供更加全面而综合的风速预测值信息。
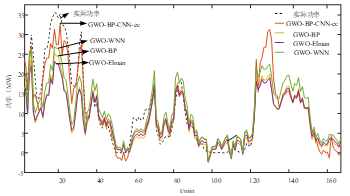
图11 深层、浅层网络预测对比
参考文献:
[1]牛哲文,余泽远,李波,唐文虎. 基于深度门控循环单元神经网络的短期风功率预测模型[J]. 电力自动化设备,2018,38(05):36-42.
[2]薛阳,王琳,王舒,张亚飞,张宁. 一种结合CNN和GRU网络的超短期风电预测模型[J]. 可再生能源,2019,37(03):456-462.
[3]张晓凤,王秀英. 灰狼优化算法研究综述[J]. 计算机科学,2019,46(03):30-38.
[4]郭振洲,刘然,拱长青,赵亮. 基于灰狼算法的改进研究[J]. 计算机应用研究,2017,34(12):3603-3606+3610.
[5]王静, 李维德. 基于 CEEMD 和 GWO 的超短期风速预测[J]. 电力系统保护与控制, 2018, 46(9): 69-74. WANG Jing, LI Weide. Ultra-short-term forecasting of wind speed based on CEEMD and GWO[J]. Power System Protection and Control, 2018, 46(9): 69-74.
[6] 董朕, 殷豪, 孟安波. 基于混合算法优化神经网络的风电预测模型[J]. 广东电力, 2017, 30(2): 29-33. DONG Zhen, YIN Hao, MENG Anbo. Wind power forecasting model based on optimized neural network of hybird algorithm[J]. Guangdong Electric Power, 2017, 30(2): 29-33.
[7] 叶燕飞, 王琦, 陈宁, 等. 考虑时空分布特性的风速预测模型[J]. 电力系统保护与控制, 2017, 45(4): 114-120. YE Yanfei, WANG Qi, CHEN Ning, et al. Wind forecast model considering the characteristics of temporal and spatial distribution[J]. Power System Protection and Control, 2017, 45(4): 114-120.
[8] Yatiyana E,Rajakaruna S,Ghosh A.Wind speed anddirection forecasting for wind power generation using ARIMA model[A].2017 Australasian Universities Power Engineering Conference (AUPEC)[C].Melbourne:IEEE,2017.1-6.
[9] 杨茂,黄宾阳,江博,等.基于卡尔曼滤波和支持向量机的风电功率实时预测研究[J].东北电力大学学报,2017,37(2):45-51.
[10]江岳 春,杨 旭 琼,贺 飞,等.基 于 EEMD-IGSA-LSSVM的超短期风电功率预测[J].湖 南 大 学 学 报(自 然 科 学版),2016,43(10):70-78.
[11] 王一珺,贾嵘.基 于 Elman 和实测风速功率数据的短期风功率预测[J].高压电器,2017,53(9):125-129
[12] 杨正瓴, 刘阳, 张泽, 等. 采用最近历史观测值和 PLSR进行空间相关性超短期风速预测[J]. 电网技术, 2017, 41(6): 1816-1822. YANG Zhengling, LIU Yang, ZHANG Ze, et al. Ultra-short-term wind speed prediction with spatial correlation using recent historical observations and PLSR[J]. Power System Technology, 2017, 41(6): 1816-1822.
[5] SONG Z, JIANG Y, ZHANG Z. Short-term wind speed forecasting with Markov-switching model[J]. Applied Energy, 2014, 130(5): 103-112.
[6] LIU H, TIAN H, LI Y, et al. Comparison of four adaboost algorithm based artificial neural works in wind speed predictions[J]. Energy Conversion Management, 2015, 92: 67-81.
[7] 潘超, 秦本双, 何瑶, 等. 基于优化 FCM 聚类的 RELM风速预测[J]. 电网技术, 2018, 42(3): 842-848. PAN Chao, QIN Benshuang, HE Yao, et al. Wind speed forecasting of regularized ELM based on optimized FCM clustering[J]. Power System Technology, 2018, 42(3): 842-848.
[8] 刘兴杰, 岑添云, 郑文书, 等. 基于模糊粗糙集与改进聚类的神经网络风速预测[J]. 中国电机工程学报, 2014, 34(19): 3162-3169. LIU Xingjie, CEN Tianyun, ZHENG Wenshu, et al. Neural network wind speed prediction based on fuzzy rough set and improved clustering[J]. Proceedings of the CSEE, 2014, 34(19): 3162-3169.
[9] 殷豪, 董朕, 陈云龙. 基于 CEEMD 和膜计算优化支持
向量机的风速预测[J]. 电力系统保护与控制, 2017, 45(21): 27-34. YIN Hao, DONG Zhen, CHEN Yunlong. Wind speed forecasting based on complementary ensemble empirical mode decomposition and support vector regression optimized by membrane computing optimization[J]. Power System Protection and Control, 2017, 45(21): 27-34.
[10] ORTIZ-GARCIA E G, SALCEDO-SANZ S, PEREZBELLIDO A M, et al. Short-term wind speed prediction in wind farms based on banks of support vector machines[J]. Wind Energy, 2011, 14(2): 193-207.
[11] ZHANG C, ZHOU J, LI C, et al. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting[J]. Energy Conversion Management, 2017, 143: 360-376.
[12] ZHANG K, LUO M. Outlier-robust extreme learning machine for regression problems[J]. Neurocomputing, 2015, 151: 1519-1527.
[13] 李余琪, 张刚林, 甘敏. 基于函数系数自回归模型的风速时间序列预测[J]. 数学的实践与认识, 2017, 47(8): 162-166. LI Yuqi, ZHANG Ganglin, GAN Min. Wind speedprediction based on functional coefficient autoregressive models[J]. Mathematics in Practice and Theory, 2017, 47(8): 162-166.
[14] 陈昊, 王玉荣. 基于随机波动模型的短期负荷预测[J]. 电力自动化设备, 2010, 30(11): 86-89. CHEN Hao, WANG Yurong. Short-term load forecasting based on SV model[J]. Electric Power Automation Equipment, 2010, 30(11): 86-89.
(本文来自于电子产品世界第11期杂志)





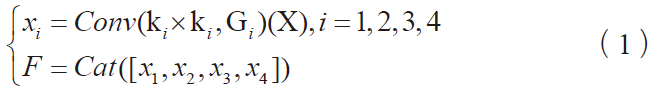

评论