人工智能之PCA算法

　　PCA算法本质：

　　PCA算法本质就是找一些投影方向，使得数据在这些投影方向上的方差最大，而且这些投影方向是相互正交的。这其实就是找新的正交基的过程，计算原始数据在这些正交基上投影的方差，方差越大，就说明在对应正交基上包含了更多的信息量。原始数据协方差矩阵的特征值越大，对应的方差越大，在对应的特征向量上投影的信息量就越大。反之，如果特征值较小，则说明数据在这些特征向量上投影的信息量很小，可以将小特征值对应方向的数据删除，从而达到了降维的目的。

　　PCA把可能具有相关性的高维变量合成线性无关的低维变量，称为主成分( principal components)。新的低维数据集会尽可能保留原始数据的变量。

　　简而言之，PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

　　PCA算法中术语：

　　1、样本“信息量”

　　样本的“信息量”指的是样本在特征方向上投影的方差。方差越大，则样本在该特征上的差异就越大，因此该特征就越重要。在分类问题里，样本的方差越大，越容易将不同类别的样本区分开。

　　2、方差

　　希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述。在统计描述中，方差用来计算每一个变量(观察值)与总体均数之间的差异。此处，一个字段的方差可以看做是每个元素与字段均值的差的平方和的均值，即：

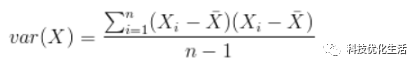
　　3、协方差

　　对于二维降成一维的问题来说，找到使得方差最大的方向就可以了。但是对于更高维的问题，需要用到协方差来表示其相关性。即：

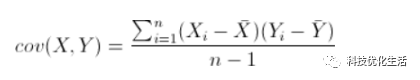
　　PCA理论基础：

　　PCA理论基础如下：

　　1)最大方差理论。

　　2)最小错误理论。

　　3)坐标轴相关度理论。

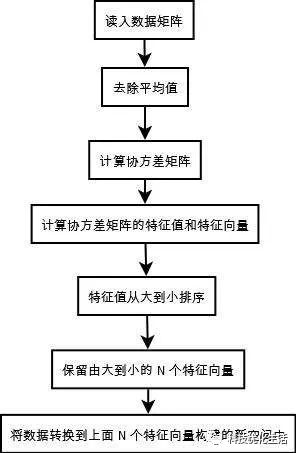
　　PCA算法流程：

　　1)去平均值，即每一位特征减去各自的平均值;

　　2)计算协方差矩阵;

　　3)计算协方差矩阵的特征值与特征向量;

　　4)对特征值从大到小排序;

　　5)保留最大的个特征向量;

　　6)将数据转换到个特征向量构建的新空间中。

　　PCA降维准则：

　　1) 最近重构性：样本集中所有点，重构后的点距离原来的点的误差之和最小。

　　2) 最大可分性：样本在低维空间的投影尽可能分开。

　　PCA算法优点：

　　1)使得数据集更易使用;

　　2)降低算法的计算开销;

　　3)去除噪声;

　　4)使得结果容易理解;

　　5)完全无参数限制。

　　PCA算法缺点：

　　1) 如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高;

　　2) 特征值分解有一些局限性，比如变换的矩阵必须是方阵;

　　3) 在非高斯分布情况下，PCA方法得出的主元可能并不是最优的。

　　PCA算法应用：

　　PCA算法已经被广泛的应用于高维数据集的探索与可视化，还可以用于数据压缩，数据预处理等领域。在机器学习当中应用很广，比如图像，语音，通信的分析处理。PCA算法最主要的用途在于“降维”，去除掉数据的一些冗余信息和噪声，使数据变得更加简单高效，提高其他机器学习任务的计算效率。

　　结语：

　　PCA是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于识别和提取数据的主要特征分量，通过将数据坐标轴旋转到数据角度上那些最重要的方向(方差最大);然后通过特征值分析，确定出需要保留的主成分个数，舍弃其他非主成分，从而实现数据的降维。降维使数据变得更加简单高效，从而实现提升数据处理速度的目的，节省大量的时间和成本。降维也成为了应用非常广泛的数据预处理方法。PCA算法已经被广泛的应用于高维数据集的探索与可视化，还可以用于数据压缩，数据预处理，图像，语音，通信的分析处理等领域。